Réduction - Problème inverse
- Objectif
- Modèle final
- Traitement statistique
- Bruits
- Signification statistique
- Exercices
- Loi du chi 2
- La vraisemblance
- Méthode des moindres carrés
- Périodogramme
Objectif
La modélisation physique du phénomène nous a permis d'obtenir un modèle 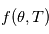 où
où 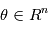 sont les paramètres du modèle et
sont les paramètres du modèle et 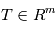 sont les instants d'observation. De nombreuses sources d'erreurs ont aussi été listées. On se pose maintenant la question suivante: comment estimer les paramètres du modèle compte tenu des observations ?
sont les instants d'observation. De nombreuses sources d'erreurs ont aussi été listées. On se pose maintenant la question suivante: comment estimer les paramètres du modèle compte tenu des observations ?
Après avoir listé diverses sources de signal et de bruits de l'émission de la lumière à la valeur donnée par le déteteur, nous allons maintenant donner une expression finale au modèle. Cette expression n'est pas universelle, et selon l'étoile observée, la précision recherchée, d'autres formulations peuvent être préférables.
Après avoir établi ce modèle, on donnera quelques principes d'analyse statistique et des moyens algorithmiques pour estimer les paramètres du modèle. On verra en particulier que l'analyse "dans le domaine fréquenciel" est particulièrement importante.
Modèle final
Le modèle comportera une partie déterministe et une partie aléatoire. Pour l'astrométrie, la position 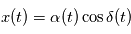
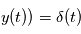 sur la sphère céleste est
sur la sphère céleste est
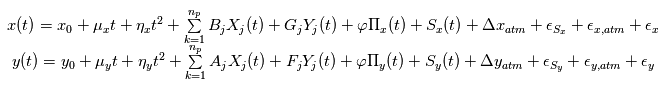
Où 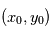 est la position initiale de l'étoile,
est la position initiale de l'étoile, 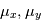 sont les composantes du mouvement propre
sont les composantes du mouvement propre 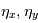 sont des termes d'accélération de perspective,
sont des termes d'accélération de perspective, 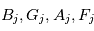 sont les constantes de Thiele-Innes de la planète
sont les constantes de Thiele-Innes de la planète 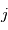 ,
, 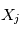 et
et 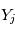 sont ses coordonnées sur son plan orbital,
sont ses coordonnées sur son plan orbital, 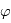 est la parallaxe,
est la parallaxe, 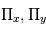 sont les coefficients parametrant le mouvement de la Terre, Les
sont les coefficients parametrant le mouvement de la Terre, Les 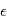 sont les bruits résiduels modélisés par des bruits gaussiens.:
sont les bruits résiduels modélisés par des bruits gaussiens.: 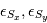 sont les bruits stellaires,
sont les bruits stellaires, 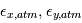 sont les bruits atmosphériques et
sont les bruits atmosphériques et 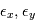 représentent des bruits instrumentaux.
représentent des bruits instrumentaux.
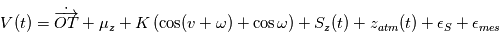
Où 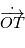 est la vitesse de l'observateur dans le référentiel barycentrique du système solaire,
est la vitesse de l'observateur dans le référentiel barycentrique du système solaire, 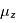 est la composante du mouvement propre dans la direction radiale,
est la composante du mouvement propre dans la direction radiale, 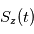 est le signal stellaire dû à la granulation, aux oscillations et à l'activité,
est le signal stellaire dû à la granulation, aux oscillations et à l'activité, 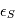 est le bruit stellaire résiduel et
est le bruit stellaire résiduel et 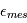 le bruit associé à la mesure.
le bruit associé à la mesure.
Dans les deux cas, les techniques de réduction de données visent à trouver des paramètres qui sont "plausibles", en l'occurrence, qui reproduisent les observations.
Traitement statistique
Rappelons qu'une variable aléatoire peut être vue comme un programme informatique qui délivre des valeurs suivant une certaine distribution de probabilité lorsqu'on lui demande. Le problème que nous posons maintenant est équivalent au suivant. Supposons qu'un ordinateur ait en mémoire des paramètres 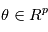 (nombre de planètes, leurs caractéristiques orbitales, la période de rotation de l'étoile etc.). S'il n'y avait pas de bruit, une mesure à l'instant
(nombre de planètes, leurs caractéristiques orbitales, la période de rotation de l'étoile etc.). S'il n'y avait pas de bruit, une mesure à l'instant 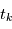 reviendrait à demander à l'ordinateur d'évaluer une fonction
reviendrait à demander à l'ordinateur d'évaluer une fonction 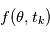 . Nous connaissons
. Nous connaissons 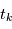 et
et 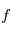 (c'est l'un des modèles de la page précédente), mais nous ne connaissons pas
(c'est l'un des modèles de la page précédente), mais nous ne connaissons pas 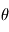 . Notre but est de le déterminer à partir des mesures
. Notre but est de le déterminer à partir des mesures 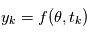 . Ce principe est similaire à la résolution d'une énigme: quelqu'un connaît une information
. Ce principe est similaire à la résolution d'une énigme: quelqu'un connaît une information 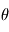 et nous essayons de la deviner en posant une question. Dans le cas sans bruit, celui qui pose l'énigme ne nous induit pas en erreur, mais cela ne veut pas dire que la résolution est facile !
et nous essayons de la deviner en posant une question. Dans le cas sans bruit, celui qui pose l'énigme ne nous induit pas en erreur, mais cela ne veut pas dire que la résolution est facile !
Exemple: on veut trouver les paramètres d'une fonction affine du temps 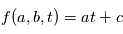 (ici
(ici 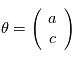 ). On évalue la valeur de
). On évalue la valeur de 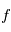 en
en 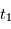 , on obtient
, on obtient 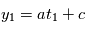 : on a deux inconnues pour une équation, on ne peut pas résoudre. Si on a
: on a deux inconnues pour une équation, on ne peut pas résoudre. Si on a 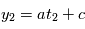 , avec
, avec 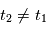 , alors on a
, alors on a 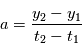 et
et 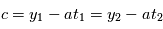 .
.
Notre cas est plus compliqué. Les valeurs que nous obtenons sont 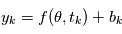 où
où 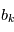 est la réalisation d'une variable aléatoire
est la réalisation d'une variable aléatoire 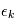 . A l'appel numéro
. A l'appel numéro 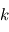 du programme, l'ordinateur fait appel à un autre programme qui délivre une variable alétoire selon une certaine loi. En l'occurrence, nous supposons cette loi gaussienne. Si nous faisons
du programme, l'ordinateur fait appel à un autre programme qui délivre une variable alétoire selon une certaine loi. En l'occurrence, nous supposons cette loi gaussienne. Si nous faisons 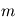 mesures, tout se passe comme si un programme principal évaluait la fonction
mesures, tout se passe comme si un programme principal évaluait la fonction 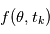 et
et 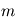 programmes secondaires
programmes secondaires 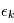 ,
, 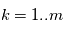 retournent chacun une valeur
retournent chacun une valeur 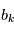 . Si nous pouvions remonter le temps et faire les mesures plusieurs fois aux mêmes instants, on aurait des des vecteurs de mesures
. Si nous pouvions remonter le temps et faire les mesures plusieurs fois aux mêmes instants, on aurait des des vecteurs de mesures 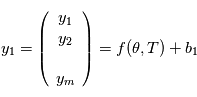 , puis
, puis 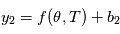 etc. (notez qu'ici
etc. (notez qu'ici 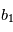 et
et 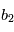 sont des vecteurs.
sont des vecteurs.
Comme nous ne connaissons que la loi suivie par les variables 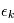 , ils nous est impossible de connaître les paramètres avec certitude. On leur attache une "erreur", qui quantifie l'incertitude que l'on a sur eux. En reprenant l'exemple précédent on mesure
, ils nous est impossible de connaître les paramètres avec certitude. On leur attache une "erreur", qui quantifie l'incertitude que l'on a sur eux. En reprenant l'exemple précédent on mesure 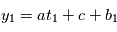 et
et 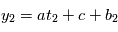 . Si on estime
. Si on estime 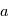 et
et 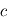 avec les mêmes formules, on fera une erreur
avec les mêmes formules, on fera une erreur 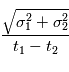 sur
sur 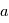 et une erreur
et une erreur 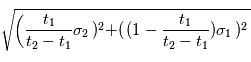 sur
sur 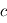 (admis).
(admis).
Bruits
Dans le modèle 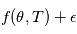 , le symbole
, le symbole 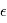 désigne un bruit gaussien. Comme ils apparaissent constamment en détection de planètes extrasolaires et ailleurs, nous allons en donner quelques propriétés.
désigne un bruit gaussien. Comme ils apparaissent constamment en détection de planètes extrasolaires et ailleurs, nous allons en donner quelques propriétés.
A une expérience donnée, 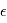 prendra une valeur
prendra une valeur 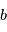 imprévisible. La probabilité que la valeur de
imprévisible. La probabilité que la valeur de 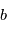 soit comprise entre
soit comprise entre 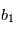 et
et 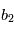 est
est 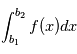 où
où 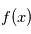 est la densité de probabilité de
est la densité de probabilité de 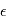 . Dire que
. Dire que 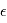 est un bruit gaussien veut dire que sa densité est de la forme
est un bruit gaussien veut dire que sa densité est de la forme 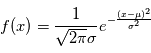 où
où 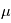 et
et 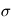 sont des réels, qui sont égaux respectivement à la moyenne et à l'écart-type de
sont des réels, qui sont égaux respectivement à la moyenne et à l'écart-type de 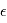 . On note souvent
. On note souvent 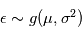 , qui signifie "
, qui signifie "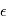 suit une loi gaussienne de moyenne
suit une loi gaussienne de moyenne 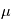 et de variance
et de variance 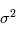 . Dans la plupart des cas, le bruit est de moyenne nulle (c'est le cas ici).
. Dans la plupart des cas, le bruit est de moyenne nulle (c'est le cas ici).
Dans le modèle, des bruits d'origines différentes s'additionnent. Sachant que le résidu de l'activité stellaire que nous n'avons pas ajusté 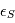 et le bruit de mesure
et le bruit de mesure 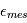 suiven une certaine loi, quelle loi suivra
suiven une certaine loi, quelle loi suivra 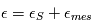 ? Nous pouvons déjà dire que la moyenne de
? Nous pouvons déjà dire que la moyenne de 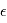 sera égale à la somme des moyennes de
sera égale à la somme des moyennes de 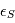 et
et 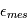 car l'espérance est un opérateur linéaire. Peut-on dire plus ? Si ces bruits dépendaient l'un de l'autre, la réponse pourrait être complexe. En l'occurrence, la physique de l'étoile cible et les erreurs instrumentales sont totalement indépendantes. On peut montrer que dans ces conditions, la variance de
car l'espérance est un opérateur linéaire. Peut-on dire plus ? Si ces bruits dépendaient l'un de l'autre, la réponse pourrait être complexe. En l'occurrence, la physique de l'étoile cible et les erreurs instrumentales sont totalement indépendantes. On peut montrer que dans ces conditions, la variance de 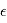 est égale à la somme des variances de
est égale à la somme des variances de 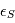 et
et 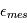 . Nous pouvons même aller plus loin car la somme de deux variables gaussiennes indépendante est une variable gaussienne. En résumé,
. Nous pouvons même aller plus loin car la somme de deux variables gaussiennes indépendante est une variable gaussienne. En résumé, 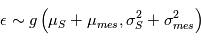 en l'occurrence
en l'occurrence 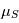 et
et 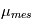 sont nulles.
sont nulles.
Lorsqu'on dispose de plusieurs mesures, à l'expérience numéro 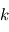 on a un certain bruit
on a un certain bruit 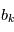 réalisation d'une variable
réalisation d'une variable 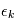 de densité
de densité 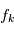 . La plupart du temps, on fait l'hypothèse que les brutis
. La plupart du temps, on fait l'hypothèse que les brutis 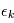 sont indépendants, c'est à dire que la probabilité d'obtenir le bruit
sont indépendants, c'est à dire que la probabilité d'obtenir le bruit 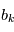 à l'expérience
à l'expérience 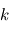 ne dépend pas des valeurs prises aux expériences précédentes et suivantes. Lorsque ce n'est pas le cas on parle de bruits corrélés. Pour les caractériser, on utilise souvent leur densité spectrale de puissance. Un certain profil de densité spectrale correspond à une "couleur" du bruit.
ne dépend pas des valeurs prises aux expériences précédentes et suivantes. Lorsque ce n'est pas le cas on parle de bruits corrélés. Pour les caractériser, on utilise souvent leur densité spectrale de puissance. Un certain profil de densité spectrale correspond à une "couleur" du bruit.
A retenir: la somme de variables gaussienne indépendantes 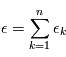 où
où 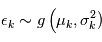 est une variable gaussienne suivant la loi
est une variable gaussienne suivant la loi 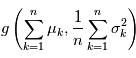 .
.
Signification statistique
Il esiste plusieurs outils pour s'assurer qu'une détection possible n'est pas due au bruit. L'un des plus utilisé est le test de signification (significance en anglais), qui consiste à calculer la probabilité d'avoir le signal observé "au moins aussi grand" s'il n'y avait en réalité que du bruit. Par exemple, qupposons que l'on veuille mesurer une quantité 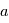 qui est perturbée par un bruit gaussien additif
qui est perturbée par un bruit gaussien additif 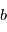 de moyenne nulle et d'écart-type
de moyenne nulle et d'écart-type 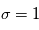 , donnant une mesure
, donnant une mesure 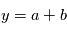 .
.
Si il n'y avait en réalité pas de signal (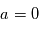 ), les mesures seraient uniquement dues au bruit. On imagine deux cas de figures:
), les mesures seraient uniquement dues au bruit. On imagine deux cas de figures:
- 1er cas: on mesure
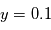 . La probabilité d'avoir obtenue une valeur au moins aussi grande par hasard, c'est à dire la probabilité que
. La probabilité d'avoir obtenue une valeur au moins aussi grande par hasard, c'est à dire la probabilité que 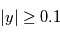 sachant que
sachant que 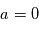 est
est 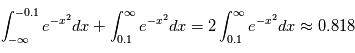
- 2ème cas: on mesure
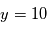 . La probabilité pour que
. La probabilité pour que 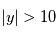 alors que
alors que 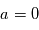 est
est 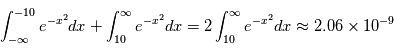
Ces valeurs ont une interprétation: si on réalisait exactement le même type de mesure alors qu'il n'y a pas de signal, on observerait 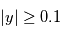 dans
dans 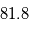 % des cas et
% des cas et 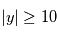 dans
dans 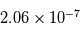 % des cas.Dans le premier cas, la probabilité d'avoir un signal aussi grand que celui que l'on a mesuré est grande. On ne peut pas assurer qu'un signal a été détecté. Par contre, dans le deuxième cas on serait dans un des deux cas sur un milliard où le signal serait dû au bruit. On peut alors dire qu'on a détecté un signal à
% des cas.Dans le premier cas, la probabilité d'avoir un signal aussi grand que celui que l'on a mesuré est grande. On ne peut pas assurer qu'un signal a été détecté. Par contre, dans le deuxième cas on serait dans un des deux cas sur un milliard où le signal serait dû au bruit. On peut alors dire qu'on a détecté un signal à 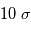 , car la valeur de l'écart-type du bruit est
, car la valeur de l'écart-type du bruit est 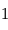 , sa moyenne est
, sa moyenne est 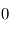 , donc on a
, donc on a 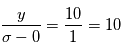 .
.
Détecter un signal "à 10 sigmas" est un luxe que l'on peut rarement se payer. Les détections sont annoncées plutôt pour des valeurs de 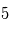 sigmas.
sigmas.
Remarque importante: on calcule la probabilité d'avoir les observations sachant qu'il n'y a pas de signal et non la probabilité d'avoir un signal sachant les observations qui est une quantité qui a davantage de sens. Le calcul de cette dernière quantité se fait dans le cadre du calcul bayésien, outil très puissant qui ne sera pas développé dans ce cours.
Exercices
Auteur: Nathan Hara
 Espérance et variance de la moyenne empirique
Espérance et variance de la moyenne empirique
Difficulté : ☆☆☆
Loi du chi 2
Nous nous sommes toujours ramenés à des modèles du type: modèle déterministe + bruit gaussien. Afin de vérifier que les observations sont compatibles avec le modèle, on étudie les résidus, définis comme "les observation - le modèle ajusté".
La loi du 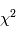 est un outil commode pour étudier le comportement de plusieurs variables gaussiennes. Considérons d'abord une famille de
est un outil commode pour étudier le comportement de plusieurs variables gaussiennes. Considérons d'abord une famille de 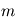 variables aléatoires gaussiennes indépendantes
variables aléatoires gaussiennes indépendantes 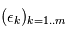 , de moyenne nulle et de variance unité. On forme la quantité
, de moyenne nulle et de variance unité. On forme la quantité 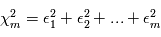 . Comme les
. Comme les 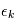 sont des variables aléatoires, les
sont des variables aléatoires, les 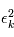 le sont aussi. La somme de variables alétoires étant toujours une variable alétoire,
le sont aussi. La somme de variables alétoires étant toujours une variable alétoire, 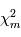 suit une certaine loi de probabilité. Dans l'analogie avec un programme informatique, la variable alétoire
suit une certaine loi de probabilité. Dans l'analogie avec un programme informatique, la variable alétoire 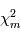 se comporte comme un programme qui appelle
se comporte comme un programme qui appelle 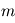 programmes générant une variables gaussiennes, puis additionne leurs carrés. Elle est appelée loi du
programmes générant une variables gaussiennes, puis additionne leurs carrés. Elle est appelée loi du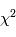 à m degrés de liberté. On peut montrer qu'en moyenne une variable gaussienne au carré
à m degrés de liberté. On peut montrer qu'en moyenne une variable gaussienne au carré 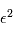 a une moyenne de 1. En conséquence,
a une moyenne de 1. En conséquence, 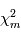 vaudra typiquement
vaudra typiquement 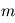 .
.
Pourquoi cette loi serait utile pour notre cas ? Si le modèle est bien ajusté, les résidus doivent se comporter comme un bruit gaussien. En supposant que les erreurs sont toutes indépendantes, de moyenne nulle et de variance unité, les résidus 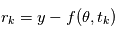 en sont une réalisation. Donc
en sont une réalisation. Donc 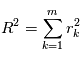 est une réalisation d'une loi du
est une réalisation d'une loi du 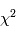 à
à 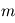 degrés de liberté. Si
degrés de liberté. Si 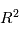 est de l'ordre de
est de l'ordre de 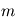 , le modèle est cohérent. Sinon, le modèle ou les paramètres ajustés sont à revoir.
, le modèle est cohérent. Sinon, le modèle ou les paramètres ajustés sont à revoir.
En pratique, les erreurs 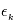 ne sont évidemment pas de variance unité et parfois pas indépendantes. Par contre on peut à bon droit supposer qu'elles sont de moyenne nulle. Pour se ramener au cas précédent, on calcule non pas une réalisation de
ne sont évidemment pas de variance unité et parfois pas indépendantes. Par contre on peut à bon droit supposer qu'elles sont de moyenne nulle. Pour se ramener au cas précédent, on calcule non pas une réalisation de 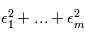 mais de
mais de 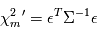 où
où 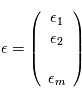 ,
, 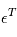 est sa transposée et
est sa transposée et 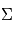 est la matrice des variances-covariances de
est la matrice des variances-covariances de 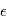 . Dans le cas où les
. Dans le cas où les 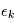 sont indépendantes, la matrice des variances-covariances est diagonale, son
sont indépendantes, la matrice des variances-covariances est diagonale, son 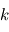 -ème terme diagonal étant
-ème terme diagonal étant 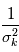 , soit l'inverse de la variance de
, soit l'inverse de la variance de 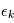 .
.
La vraisemblance
Etant donné des paramètres 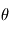 , le modèle global
, le modèle global 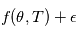 est une variable aléatoire: il est somme d'une variable aléatoire valant
est une variable aléatoire: il est somme d'une variable aléatoire valant 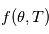 avec une probabilité 1 et d'un vecteur de variables aléatoires gaussienne
avec une probabilité 1 et d'un vecteur de variables aléatoires gaussienne 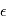 . A ce titre, il a une certaine densité de probabilité que l'on note
. A ce titre, il a une certaine densité de probabilité que l'on note 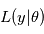 . Le symbole | se lisant "sachant". La lettre L vient de Likelihood, qui veut dire vraisemblance en anglais. Il s'agit dans l'idée de la probabilité d'obtenir
. Le symbole | se lisant "sachant". La lettre L vient de Likelihood, qui veut dire vraisemblance en anglais. Il s'agit dans l'idée de la probabilité d'obtenir 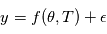 pour une valeur de
pour une valeur de 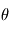 donnée..
donnée..
La fonction 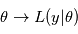 est souvent appelée "fonction de vraisemblance". La valeur de
est souvent appelée "fonction de vraisemblance". La valeur de 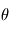 maximisant
maximisant 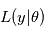 est appelé l'estimateur du maximum de vraisemblance. Il a de bonnes propritétés statistiques. En effet, on peut montrer que c'est un estimateur:
est appelé l'estimateur du maximum de vraisemblance. Il a de bonnes propritétés statistiques. En effet, on peut montrer que c'est un estimateur:
- Non biaisé: lorsque le nombre de mesure tend vers l'infini, l'estimateur du maximum de vraisemblance tend vers la bonne valeur
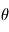
- De variance minimale: parmi les estimateurs non biaisés, il a la variance la plus faible que l'on puisse espérer.
Dans notre cas, si les 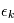 sont des variables indépendantes, leur densité de probabilité jointe est égale au produit de leurs densité de probabilité.
sont des variables indépendantes, leur densité de probabilité jointe est égale au produit de leurs densité de probabilité. 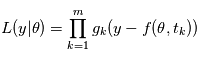 où
où 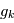 est la densité de probabilité de la variable
est la densité de probabilité de la variable 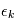 . De plus, si ces varibles sont gaussiennes et indépendantes, on a:
. De plus, si ces varibles sont gaussiennes et indépendantes, on a: 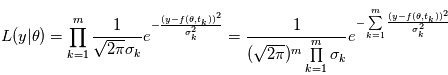
Méthode des moindres carrés
Pour des bruits gaussiens indépendants, maximiser la vraisemblance, revient à minimiser 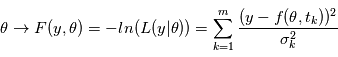 puisque
puisque 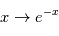 est une fonction décroissante. La méthode consistant à minimiser
est une fonction décroissante. La méthode consistant à minimiser 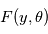 s'appelle la méthode des moindres carrés. C'est la méthode d'estimation de loin la plus utilisée dans tous les domaines. Elle est parfois utilisée quand les bruits ne sont pas gaussiens, mais il faut garder à l'esprit qu'elle n'a alors plus de propriétés statistiques sympathiques (sauf quand le modèle est linéaire en
s'appelle la méthode des moindres carrés. C'est la méthode d'estimation de loin la plus utilisée dans tous les domaines. Elle est parfois utilisée quand les bruits ne sont pas gaussiens, mais il faut garder à l'esprit qu'elle n'a alors plus de propriétés statistiques sympathiques (sauf quand le modèle est linéaire en  .
.
Dans notre cas, les paramètres  sont les éléments des orbites, les paramètres du bruit stellaire, du mouvement propre, etc. La fonction
sont les éléments des orbites, les paramètres du bruit stellaire, du mouvement propre, etc. La fonction 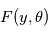 a donc de nombreux paramètres, et trouver son minimum global est une tâche ardue qui fait l'objet d'une littérature très vaste.
a donc de nombreux paramètres, et trouver son minimum global est une tâche ardue qui fait l'objet d'une littérature très vaste.
Lorsque le modèle est linéaire en 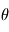 i. e.
i. e. 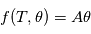 où
où 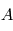 est une certaine matrice dépendant des instants d'observation
est une certaine matrice dépendant des instants d'observation 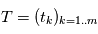 , l'ajustement est beaucoup plus simple car il a une solution explicite (voir mini-projet). On essaye de se ramener autant que possible à des ajustements linéaires. La plupart du temps, on estime les paramètre les uns après les autres, puis un ajustement global est réalisé. Une démarche classique consiste à:
, l'ajustement est beaucoup plus simple car il a une solution explicite (voir mini-projet). On essaye de se ramener autant que possible à des ajustements linéaires. La plupart du temps, on estime les paramètre les uns après les autres, puis un ajustement global est réalisé. Une démarche classique consiste à:
- Ajuster le mouvement propre et la parallaxe, puis soustraire ces ajustements du signal initial
- Chercher les périodes éventuelles dans le signal à l'aide du périogogramme (voir page suivante)
- Si on trouve une période, on ajuste une orbite, que l'on soustrait du signal
- On recommence les étapes 2 et 3 jusqu'à ce que le périodogramme ne présente plus de pic significatif
Sur la figure, on représente les étapes d'un ajustement d'un signal astrométrique simulé (2 planètes, 45 observations). De gauche à droite et de haut en bas:
- Signal brut en rouge
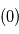 En vert signal après correction des bruits instrumentaux et atmosphériques
En vert signal après correction des bruits instrumentaux et atmosphériques 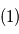 . Le mouvement propre (tendance linéaire) et la parallaxe (oscillation) dominent très nettement le signal.
. Le mouvement propre (tendance linéaire) et la parallaxe (oscillation) dominent très nettement le signal. - En vert: le signal planétaire réel, sans aucun bruit
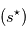 . En rouge: signal estimé
. En rouge: signal estimé 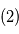 en soustrayant le mouvement propre, l'accélération de perspective et la parallaxe au signal
en soustrayant le mouvement propre, l'accélération de perspective et la parallaxe au signal 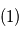 .
. - En rouge: signal
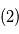 . En vert
. En vert 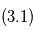 : orbite d'une planète ajustée sur
: orbite d'une planète ajustée sur 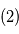 .
. - En rouge
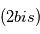 : signal
: signal 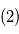 dont on a soustrait
dont on a soustrait 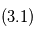 . En vert
. En vert 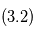 :orbite d'une planète ajustée sur
:orbite d'une planète ajustée sur 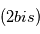 .
. - En rouge: signal
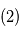 . En vert:
. En vert: 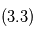 , ajustement de deux planètes en partant des estimations
, ajustement de deux planètes en partant des estimations 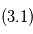 et
et 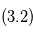 .
. - En vert, signal
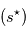 . On ajuste tous les paramètres simultanément sur
. On ajuste tous les paramètres simultanément sur 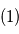 en partant des estimations précédentes. Le signal en rouge représente le signal planétaire de cet ajustement.
en partant des estimations précédentes. Le signal en rouge représente le signal planétaire de cet ajustement.
Exemple d'ajustement en astrométrie (données simulées)
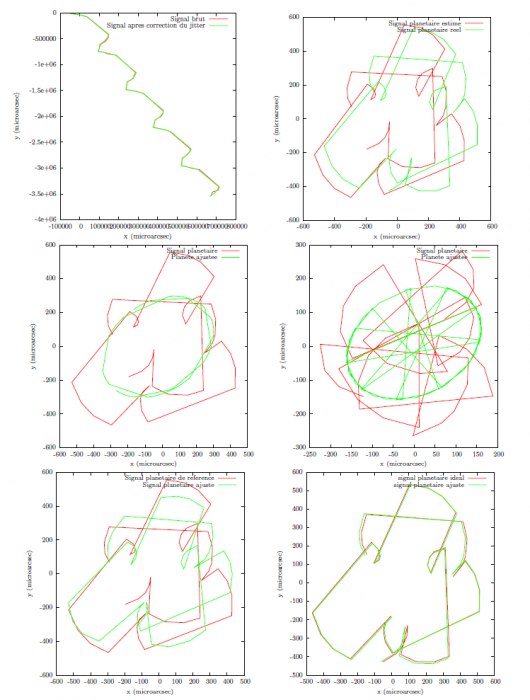
Six étapes d'ajustement aux données. Pour représenter la chronologie des mesures, on trace des segments reliant deux points de mesure consécutifs.
Périodogramme
Evaluer les résidus sur une grille d'un modèle à 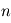 paramètres, où chacun d'eux peut prendre
paramètres, où chacun d'eux peut prendre 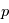 valeurs recquiert
valeurs recquiert 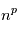 évaluations, ce qui devient rapidement ingérable numériquement. Les planètes ont un mouvement périodique, donc il est raisonnable de checher des signaux périodiques dans le signal en ne faisant varier que la période du signal recherché. Pour des signaux échantillonnés à intervalles réguliers, on utilise la transformée de Fourier. Le périodogramme est un moyen de checher des signaux périodiques dans des données échantillonnées irrégulièrement. On les notera
évaluations, ce qui devient rapidement ingérable numériquement. Les planètes ont un mouvement périodique, donc il est raisonnable de checher des signaux périodiques dans le signal en ne faisant varier que la période du signal recherché. Pour des signaux échantillonnés à intervalles réguliers, on utilise la transformée de Fourier. Le périodogramme est un moyen de checher des signaux périodiques dans des données échantillonnées irrégulièrement. On les notera 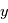 . Le périodogramme de Lomb-Scargle d'un signal
. Le périodogramme de Lomb-Scargle d'un signal 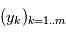 échantillonné aux instants
échantillonné aux instants 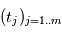 est défini comme suit pour une fréquence quelconque
est défini comme suit pour une fréquence quelconque 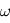 :
:
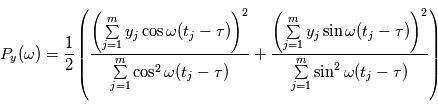 où
où 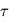 vérifie:
vérifie:
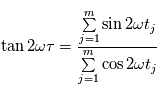
Cette expression est équivalente à 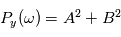 où
où 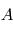 et
et 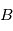 sont les paramètres minimisant
sont les paramètres minimisant 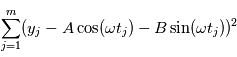 . Le modèle
. Le modèle 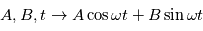 est linéaire en
est linéaire en  , on a donc une solution explicite à la minimisation.
, on a donc une solution explicite à la minimisation.
Le périodogramme a une propriété très intéressante: si le signal d'entrée est un bruit gaussien 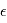 de variance unité,
de variance unité, 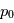 une valeur réelle fixée et
une valeur réelle fixée et 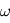 une fréquence quelconque, la probabilité que
une fréquence quelconque, la probabilité que 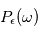 dépasse
dépasse 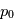 est
est 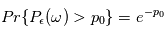 . En d'autres termes, la probabilité qu'une valeur du périodogramme à
. En d'autres termes, la probabilité qu'une valeur du périodogramme à 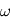 fixée soit "au moins aussi grand que
fixée soit "au moins aussi grand que 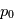 " par hasard décroît exponentiellement. Supposons que l'on ait un signal
" par hasard décroît exponentiellement. Supposons que l'on ait un signal 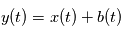 où
où 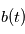 est un bruit gaussien de variance unité et nous trouvons un pic de taille
est un bruit gaussien de variance unité et nous trouvons un pic de taille 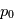 , on calcule la probabilité de trouver un pic au moins aussi grand si le signal n'est composé que de bruit:
, on calcule la probabilité de trouver un pic au moins aussi grand si le signal n'est composé que de bruit: 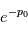 . Si cette valeur est petite, on pourra confirmer la détection d'un signal avec une erreur de fausse alarme de
. Si cette valeur est petite, on pourra confirmer la détection d'un signal avec une erreur de fausse alarme de 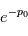 . Ce procédé n'est autre qu'un test de signification statistique.
. Ce procédé n'est autre qu'un test de signification statistique.
La figure montre un exemple de périodogramme. Il s'agit d'un périodogramme d'une des coordonnées d'un signal astrométrique simulé dont on a soustrait le mouvement propre et la parallaxe. En bleu, on représente un périodogramme idéal, sans bruit, avec 10000 observations. Le périodogramme représenté en rouge est lui calculé pour 45 observations. Le pic le plus haut correspond bien à une fréquence réelle. Par contre, le deuxième pic le plus important (à 0.37 rad/s) ne correspond pas à une sinusoïde. C'est ce qu'on appelle un alias de la fréquence principale.
En pratique, la variance du bruit n'est pas unitaire et dépend de l'instant de mesure. On peut corriger ce problème en minimisant un critère pondéré 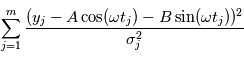 où
où 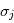 est la variance du bruit à la mesure
est la variance du bruit à la mesure 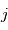 .
.
Exemple de périodogramme
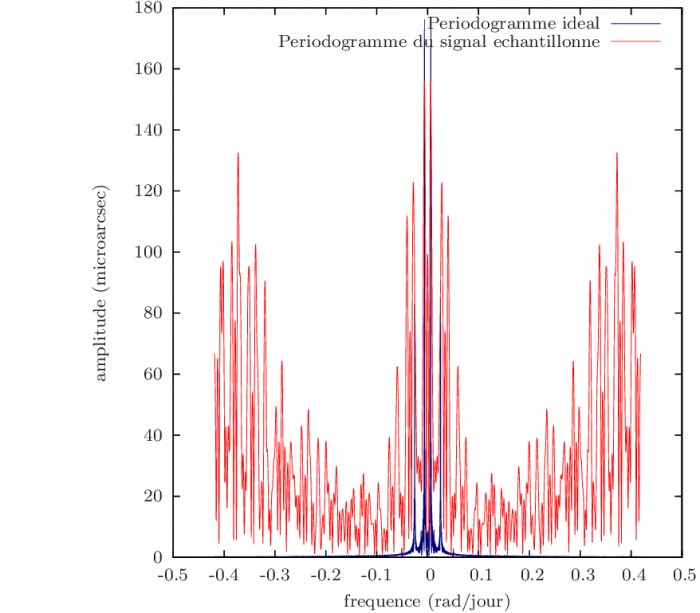
En rouge: périodogramme d'un système simulé à deux planètes après soustraction du mouvement propre et de la parallaxe (signal très peu bruité), pour 45 mesures. En bleu: périodogramme du même système sans bruit et avec 10000 observations.
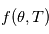 où
où 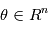 sont les paramètres du modèle et
sont les paramètres du modèle et 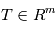 sont les instants d'observation. De nombreuses sources d'erreurs ont aussi été listées. On se pose maintenant la question suivante: comment estimer les paramètres du modèle compte tenu des observations ?
sont les instants d'observation. De nombreuses sources d'erreurs ont aussi été listées. On se pose maintenant la question suivante: comment estimer les paramètres du modèle compte tenu des observations ?
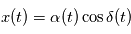
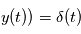 sur la sphère céleste est
sur la sphère céleste est
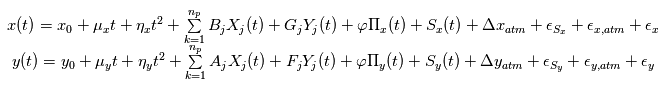
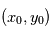 est la position initiale de l'étoile,
est la position initiale de l'étoile, 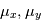 sont les composantes du mouvement propre
sont les composantes du mouvement propre 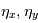 sont des termes d'accélération de perspective,
sont des termes d'accélération de perspective, 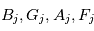 sont les constantes de Thiele-Innes de la planète
sont les constantes de Thiele-Innes de la planète 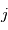 ,
, 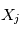 et
et 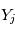 sont ses coordonnées sur son plan orbital,
sont ses coordonnées sur son plan orbital, 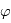 est la parallaxe,
est la parallaxe, 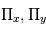 sont les coefficients parametrant le mouvement de la Terre, Les
sont les coefficients parametrant le mouvement de la Terre, Les 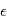 sont les bruits résiduels modélisés par des bruits gaussiens.:
sont les bruits résiduels modélisés par des bruits gaussiens.: 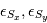 sont les bruits stellaires,
sont les bruits stellaires, 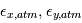 sont les bruits atmosphériques et
sont les bruits atmosphériques et 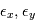 représentent des bruits instrumentaux.
représentent des bruits instrumentaux.
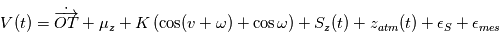
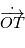 est la vitesse de l'observateur dans le référentiel barycentrique du système solaire,
est la vitesse de l'observateur dans le référentiel barycentrique du système solaire, 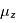 est la composante du mouvement propre dans la direction radiale,
est la composante du mouvement propre dans la direction radiale, 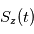 est le signal stellaire dû à la granulation, aux oscillations et à l'activité,
est le signal stellaire dû à la granulation, aux oscillations et à l'activité, 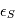 est le bruit stellaire résiduel et
est le bruit stellaire résiduel et 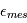 le bruit associé à la mesure.
le bruit associé à la mesure.
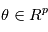 (nombre de planètes, leurs caractéristiques orbitales, la période de rotation de l'étoile etc.). S'il n'y avait pas de bruit, une mesure à l'instant
(nombre de planètes, leurs caractéristiques orbitales, la période de rotation de l'étoile etc.). S'il n'y avait pas de bruit, une mesure à l'instant 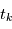 reviendrait à demander à l'ordinateur d'évaluer une fonction
reviendrait à demander à l'ordinateur d'évaluer une fonction 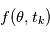 . Nous connaissons
. Nous connaissons 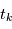 et
et 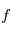 (c'est l'un des modèles de la page précédente), mais nous ne connaissons pas
(c'est l'un des modèles de la page précédente), mais nous ne connaissons pas 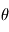 . Notre but est de le déterminer à partir des mesures
. Notre but est de le déterminer à partir des mesures 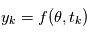 . Ce principe est similaire à la résolution d'une énigme: quelqu'un connaît une information
. Ce principe est similaire à la résolution d'une énigme: quelqu'un connaît une information 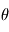 et nous essayons de la deviner en posant une question. Dans le cas sans bruit, celui qui pose l'énigme ne nous induit pas en erreur, mais cela ne veut pas dire que la résolution est facile !
et nous essayons de la deviner en posant une question. Dans le cas sans bruit, celui qui pose l'énigme ne nous induit pas en erreur, mais cela ne veut pas dire que la résolution est facile !
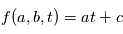 (ici
(ici 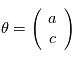 ). On évalue la valeur de
). On évalue la valeur de 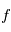 en
en 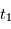 , on obtient
, on obtient 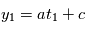 : on a deux inconnues pour une équation, on ne peut pas résoudre. Si on a
: on a deux inconnues pour une équation, on ne peut pas résoudre. Si on a 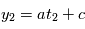 , avec
, avec 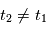 , alors on a
, alors on a 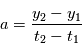 et
et 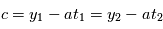 .
.
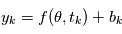 où
où 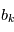 est la réalisation d'une variable aléatoire
est la réalisation d'une variable aléatoire 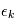 . A l'appel numéro
. A l'appel numéro 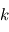 du programme, l'ordinateur fait appel à un autre programme qui délivre une variable alétoire selon une certaine loi. En l'occurrence, nous supposons cette loi gaussienne. Si nous faisons
du programme, l'ordinateur fait appel à un autre programme qui délivre une variable alétoire selon une certaine loi. En l'occurrence, nous supposons cette loi gaussienne. Si nous faisons 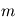 mesures, tout se passe comme si un programme principal évaluait la fonction
mesures, tout se passe comme si un programme principal évaluait la fonction 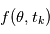 et
et 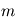 programmes secondaires
programmes secondaires 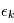 ,
, 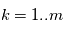 retournent chacun une valeur
retournent chacun une valeur 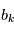 . Si nous pouvions remonter le temps et faire les mesures plusieurs fois aux mêmes instants, on aurait des des vecteurs de mesures
. Si nous pouvions remonter le temps et faire les mesures plusieurs fois aux mêmes instants, on aurait des des vecteurs de mesures 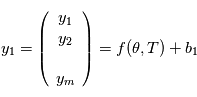 , puis
, puis 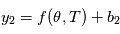 etc. (notez qu'ici
etc. (notez qu'ici 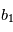 et
et 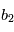 sont des vecteurs.
sont des vecteurs.
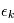 , ils nous est impossible de connaître les paramètres avec certitude. On leur attache une "erreur", qui quantifie l'incertitude que l'on a sur eux. En reprenant l'exemple précédent on mesure
, ils nous est impossible de connaître les paramètres avec certitude. On leur attache une "erreur", qui quantifie l'incertitude que l'on a sur eux. En reprenant l'exemple précédent on mesure 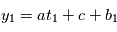 et
et 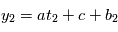 . Si on estime
. Si on estime 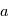 et
et 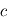 avec les mêmes formules, on fera une erreur
avec les mêmes formules, on fera une erreur 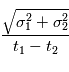 sur
sur 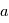 et une erreur
et une erreur 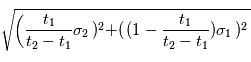 sur
sur 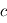 (admis).
(admis).
 , le symbole
, le symbole  désigne un bruit gaussien. Comme ils apparaissent constamment en détection de planètes extrasolaires et ailleurs, nous allons en donner quelques propriétés.
désigne un bruit gaussien. Comme ils apparaissent constamment en détection de planètes extrasolaires et ailleurs, nous allons en donner quelques propriétés.
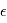 prendra une valeur
prendra une valeur 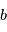 imprévisible. La probabilité que la valeur de
imprévisible. La probabilité que la valeur de 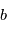 soit comprise entre
soit comprise entre 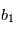 et
et 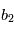 est
est 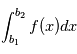 où
où 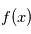 est la densité de probabilité de
est la densité de probabilité de 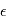 . Dire que
. Dire que 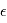 est un bruit gaussien veut dire que sa densité est de la forme
est un bruit gaussien veut dire que sa densité est de la forme 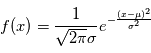 où
où 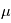 et
et 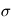 sont des réels, qui sont égaux respectivement à la moyenne et à l'écart-type de
sont des réels, qui sont égaux respectivement à la moyenne et à l'écart-type de 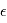 . On note souvent
. On note souvent 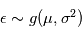 , qui signifie "
, qui signifie "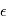 suit une loi gaussienne de moyenne
suit une loi gaussienne de moyenne 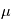 et de variance
et de variance 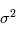 . Dans la plupart des cas, le bruit est de moyenne nulle (c'est le cas ici).
. Dans la plupart des cas, le bruit est de moyenne nulle (c'est le cas ici).
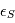 et le bruit de mesure
et le bruit de mesure 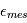 suiven une certaine loi, quelle loi suivra
suiven une certaine loi, quelle loi suivra 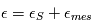 ? Nous pouvons déjà dire que la moyenne de
? Nous pouvons déjà dire que la moyenne de 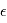 sera égale à la somme des moyennes de
sera égale à la somme des moyennes de 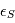 et
et 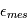 car l'espérance est un opérateur linéaire. Peut-on dire plus ? Si ces bruits dépendaient l'un de l'autre, la réponse pourrait être complexe. En l'occurrence, la physique de l'étoile cible et les erreurs instrumentales sont totalement indépendantes. On peut montrer que dans ces conditions, la variance de
car l'espérance est un opérateur linéaire. Peut-on dire plus ? Si ces bruits dépendaient l'un de l'autre, la réponse pourrait être complexe. En l'occurrence, la physique de l'étoile cible et les erreurs instrumentales sont totalement indépendantes. On peut montrer que dans ces conditions, la variance de 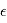 est égale à la somme des variances de
est égale à la somme des variances de 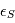 et
et 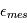 . Nous pouvons même aller plus loin car la somme de deux variables gaussiennes indépendante est une variable gaussienne. En résumé,
. Nous pouvons même aller plus loin car la somme de deux variables gaussiennes indépendante est une variable gaussienne. En résumé, 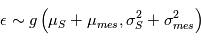 en l'occurrence
en l'occurrence 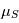 et
et 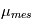 sont nulles.
sont nulles.
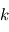 on a un certain bruit
on a un certain bruit 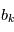 réalisation d'une variable
réalisation d'une variable 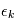 de densité
de densité 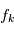 . La plupart du temps, on fait l'hypothèse que les brutis
. La plupart du temps, on fait l'hypothèse que les brutis 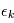 sont indépendants, c'est à dire que la probabilité d'obtenir le bruit
sont indépendants, c'est à dire que la probabilité d'obtenir le bruit 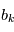 à l'expérience
à l'expérience 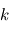 ne dépend pas des valeurs prises aux expériences précédentes et suivantes. Lorsque ce n'est pas le cas on parle de bruits corrélés. Pour les caractériser, on utilise souvent leur
ne dépend pas des valeurs prises aux expériences précédentes et suivantes. Lorsque ce n'est pas le cas on parle de bruits corrélés. Pour les caractériser, on utilise souvent leur 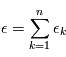 où
où 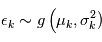 est une variable gaussienne suivant la loi
est une variable gaussienne suivant la loi 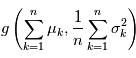 .
.
 qui est perturbée par un bruit gaussien additif
qui est perturbée par un bruit gaussien additif 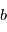 de moyenne nulle et d'écart-type
de moyenne nulle et d'écart-type 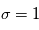 , donnant une mesure
, donnant une mesure 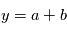 .
.
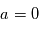 ), les mesures seraient uniquement dues au bruit. On imagine deux cas de figures:
), les mesures seraient uniquement dues au bruit. On imagine deux cas de figures:
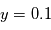 . La probabilité d'avoir obtenue une valeur au moins aussi grande par hasard, c'est à dire la probabilité que
. La probabilité d'avoir obtenue une valeur au moins aussi grande par hasard, c'est à dire la probabilité que 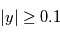 sachant que
sachant que 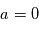 est
est 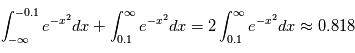
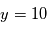 . La probabilité pour que
. La probabilité pour que 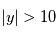 alors que
alors que 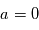 est
est 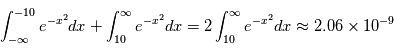
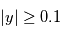 dans
dans 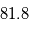 % des cas et
% des cas et 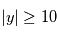 dans
dans 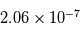 % des cas.Dans le premier cas, la probabilité d'avoir un signal aussi grand que celui que l'on a mesuré est grande. On ne peut pas assurer qu'un signal a été détecté. Par contre, dans le deuxième cas on serait dans un des deux cas sur un milliard où le signal serait dû au bruit. On peut alors dire qu'on a détecté un signal à
% des cas.Dans le premier cas, la probabilité d'avoir un signal aussi grand que celui que l'on a mesuré est grande. On ne peut pas assurer qu'un signal a été détecté. Par contre, dans le deuxième cas on serait dans un des deux cas sur un milliard où le signal serait dû au bruit. On peut alors dire qu'on a détecté un signal à 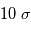 , car la valeur de l'écart-type du bruit est
, car la valeur de l'écart-type du bruit est 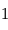 , sa moyenne est
, sa moyenne est 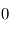 , donc on a
, donc on a 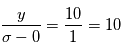 .
.
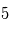 sigmas.
sigmas.
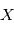 de densité de probabilité
de densité de probabilité 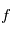 sont données par
sont données par 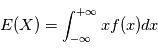 et
et 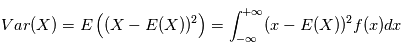
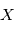 une variable aléatoire et
une variable aléatoire et 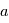 un réel. Montrer que
un réel. Montrer que 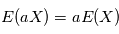 et
et 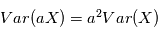
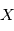 et
et 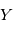 deux variables aléatoires indépendantes. Montrer que
deux variables aléatoires indépendantes. Montrer que 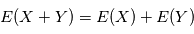 .
.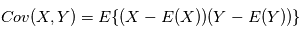 . Montrer que
. Montrer que 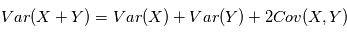
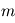 mesures entachées de bruits gaussiens d'une quantité fixe
mesures entachées de bruits gaussiens d'une quantité fixe 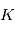 . Plus précisément, la mesure numéro
. Plus précisément, la mesure numéro 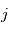 est modélisée par une variable aléatoire
est modélisée par une variable aléatoire 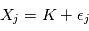 où
où 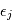 est un bruit gaussien de moyenne nulle et de variance
est un bruit gaussien de moyenne nulle et de variance 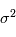 . On suppose que les mesures sont indépendantes, ce qui implique en particulier que
. On suppose que les mesures sont indépendantes, ce qui implique en particulier que 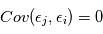 pour
pour 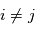 . Pour obtenir une estimation de
. Pour obtenir une estimation de 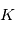 , on fait la moyenne empirique des expériences, c'est à dire
, on fait la moyenne empirique des expériences, c'est à dire 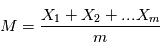 . Montrer que
. Montrer que 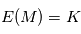 et
et 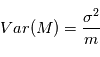
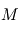 augmente-t-elle avec le nombre de mesures ?
augmente-t-elle avec le nombre de mesures ? 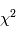 est un outil commode pour étudier le comportement de plusieurs variables gaussiennes. Considérons d'abord une famille de
est un outil commode pour étudier le comportement de plusieurs variables gaussiennes. Considérons d'abord une famille de 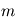 variables aléatoires gaussiennes indépendantes
variables aléatoires gaussiennes indépendantes 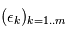 , de moyenne nulle et de variance unité. On forme la quantité
, de moyenne nulle et de variance unité. On forme la quantité 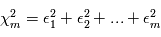 . Comme les
. Comme les 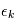 sont des variables aléatoires, les
sont des variables aléatoires, les 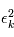 le sont aussi. La somme de variables alétoires étant toujours une variable alétoire,
le sont aussi. La somme de variables alétoires étant toujours une variable alétoire, 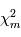 suit une certaine loi de probabilité. Dans l'analogie avec un programme informatique, la variable alétoire
suit une certaine loi de probabilité. Dans l'analogie avec un programme informatique, la variable alétoire 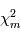 se comporte comme un programme qui appelle
se comporte comme un programme qui appelle 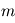 programmes générant une variables gaussiennes, puis additionne leurs carrés. Elle est appelée loi du
programmes générant une variables gaussiennes, puis additionne leurs carrés. Elle est appelée loi du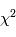 à m degrés de liberté. On peut montrer qu'en moyenne une variable gaussienne au carré
à m degrés de liberté. On peut montrer qu'en moyenne une variable gaussienne au carré 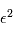 a une moyenne de 1. En conséquence,
a une moyenne de 1. En conséquence, 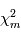 vaudra typiquement
vaudra typiquement 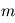 .
.
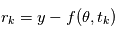 en sont une réalisation. Donc
en sont une réalisation. Donc 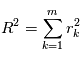 est une réalisation d'une loi du
est une réalisation d'une loi du 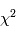 à
à 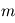 degrés de liberté. Si
degrés de liberté. Si 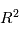 est de l'ordre de
est de l'ordre de 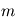 , le modèle est cohérent. Sinon, le modèle ou les paramètres ajustés sont à revoir.
, le modèle est cohérent. Sinon, le modèle ou les paramètres ajustés sont à revoir.
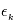 ne sont évidemment pas de variance unité et parfois pas indépendantes. Par contre on peut à bon droit supposer qu'elles sont de moyenne nulle. Pour se ramener au cas précédent, on calcule non pas une réalisation de
ne sont évidemment pas de variance unité et parfois pas indépendantes. Par contre on peut à bon droit supposer qu'elles sont de moyenne nulle. Pour se ramener au cas précédent, on calcule non pas une réalisation de 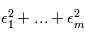 mais de
mais de 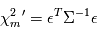 où
où 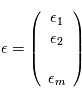 ,
, 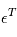 est sa transposée et
est sa transposée et 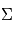 est la matrice des variances-covariances de
est la matrice des variances-covariances de 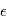 . Dans le cas où les
. Dans le cas où les 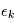 sont indépendantes, la matrice des variances-covariances est diagonale, son
sont indépendantes, la matrice des variances-covariances est diagonale, son 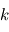 -ème terme diagonal étant
-ème terme diagonal étant 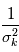 , soit l'inverse de la variance de
, soit l'inverse de la variance de 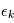 .
.
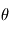 , le modèle global
, le modèle global 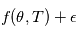 est une variable aléatoire: il est somme d'une variable aléatoire valant
est une variable aléatoire: il est somme d'une variable aléatoire valant 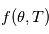 avec une probabilité 1 et d'un vecteur de variables aléatoires gaussienne
avec une probabilité 1 et d'un vecteur de variables aléatoires gaussienne 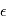 . A ce titre, il a une certaine densité de probabilité que l'on note
. A ce titre, il a une certaine densité de probabilité que l'on note 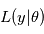 . Le symbole | se lisant "sachant". La lettre L vient de Likelihood, qui veut dire vraisemblance en anglais. Il s'agit dans l'idée de la probabilité d'obtenir
. Le symbole | se lisant "sachant". La lettre L vient de Likelihood, qui veut dire vraisemblance en anglais. Il s'agit dans l'idée de la probabilité d'obtenir 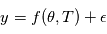 pour une valeur de
pour une valeur de 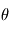 donnée..
donnée..
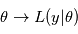 est souvent appelée "fonction de vraisemblance". La valeur de
est souvent appelée "fonction de vraisemblance". La valeur de 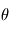 maximisant
maximisant 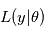 est appelé l'estimateur du maximum de vraisemblance. Il a de bonnes propritétés statistiques. En effet, on peut montrer que c'est un estimateur:
est appelé l'estimateur du maximum de vraisemblance. Il a de bonnes propritétés statistiques. En effet, on peut montrer que c'est un estimateur:
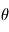
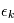 sont des variables indépendantes, leur densité de probabilité jointe est égale au produit de leurs densité de probabilité.
sont des variables indépendantes, leur densité de probabilité jointe est égale au produit de leurs densité de probabilité. 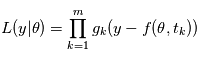 où
où 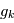 est la densité de probabilité de la variable
est la densité de probabilité de la variable 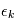 . De plus, si ces varibles sont gaussiennes et indépendantes, on a:
. De plus, si ces varibles sont gaussiennes et indépendantes, on a: 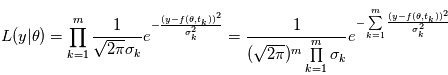
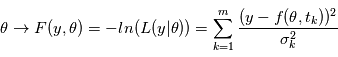 puisque
puisque 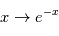 est une fonction décroissante. La méthode consistant à minimiser
est une fonction décroissante. La méthode consistant à minimiser  s'appelle la méthode des moindres carrés. C'est la méthode d'estimation de loin la plus utilisée dans tous les domaines. Elle est parfois utilisée quand les bruits ne sont pas gaussiens, mais il faut garder à l'esprit qu'elle n'a alors plus de propriétés statistiques sympathiques (sauf quand le modèle est linéaire en
s'appelle la méthode des moindres carrés. C'est la méthode d'estimation de loin la plus utilisée dans tous les domaines. Elle est parfois utilisée quand les bruits ne sont pas gaussiens, mais il faut garder à l'esprit qu'elle n'a alors plus de propriétés statistiques sympathiques (sauf quand le modèle est linéaire en 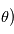 .
.
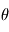 sont les éléments des orbites, les paramètres du bruit stellaire, du mouvement propre, etc. La fonction
sont les éléments des orbites, les paramètres du bruit stellaire, du mouvement propre, etc. La fonction 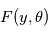 a donc de nombreux paramètres, et trouver son minimum global est une tâche ardue qui fait l'objet d'une littérature très vaste.
a donc de nombreux paramètres, et trouver son minimum global est une tâche ardue qui fait l'objet d'une littérature très vaste.
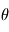 i. e.
i. e. 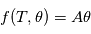 où
où 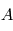 est une certaine matrice dépendant des instants d'observation
est une certaine matrice dépendant des instants d'observation 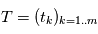 , l'ajustement est beaucoup plus simple car il a une solution explicite (voir mini-projet). On essaye de se ramener autant que possible à des ajustements linéaires. La plupart du temps, on estime les paramètre les uns après les autres, puis un ajustement global est réalisé. Une démarche classique consiste à:
, l'ajustement est beaucoup plus simple car il a une solution explicite (voir mini-projet). On essaye de se ramener autant que possible à des ajustements linéaires. La plupart du temps, on estime les paramètre les uns après les autres, puis un ajustement global est réalisé. Une démarche classique consiste à:
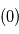 En vert signal après correction des bruits instrumentaux et atmosphériques
En vert signal après correction des bruits instrumentaux et atmosphériques 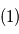 . Le mouvement propre (tendance linéaire) et la parallaxe (oscillation) dominent très nettement le signal.
. Le mouvement propre (tendance linéaire) et la parallaxe (oscillation) dominent très nettement le signal.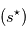 . En rouge: signal estimé
. En rouge: signal estimé 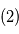 en soustrayant le mouvement propre, l'accélération de perspective et la parallaxe au signal
en soustrayant le mouvement propre, l'accélération de perspective et la parallaxe au signal 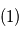 .
.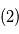 . En vert
. En vert 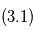 : orbite d'une planète ajustée sur
: orbite d'une planète ajustée sur 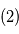 .
.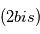 : signal
: signal 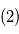 dont on a soustrait
dont on a soustrait 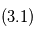 . En vert
. En vert 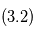 :orbite d'une planète ajustée sur
:orbite d'une planète ajustée sur 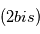 .
.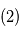 . En vert:
. En vert: 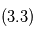 , ajustement de deux planètes en partant des estimations
, ajustement de deux planètes en partant des estimations 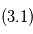 et
et 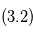 .
.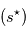 . On ajuste tous les paramètres simultanément sur
. On ajuste tous les paramètres simultanément sur 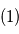 en partant des estimations précédentes. Le signal en rouge représente le signal planétaire de cet ajustement.
en partant des estimations précédentes. Le signal en rouge représente le signal planétaire de cet ajustement.
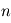 paramètres, où chacun d'eux peut prendre
paramètres, où chacun d'eux peut prendre 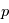 valeurs recquiert
valeurs recquiert 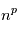 évaluations, ce qui devient rapidement ingérable numériquement. Les planètes ont un mouvement périodique, donc il est raisonnable de checher des signaux périodiques dans le signal en ne faisant varier que la période du signal recherché. Pour des signaux échantillonnés à intervalles réguliers, on utilise la transformée de Fourier. Le périodogramme est un moyen de checher des signaux périodiques dans des données échantillonnées irrégulièrement. On les notera
évaluations, ce qui devient rapidement ingérable numériquement. Les planètes ont un mouvement périodique, donc il est raisonnable de checher des signaux périodiques dans le signal en ne faisant varier que la période du signal recherché. Pour des signaux échantillonnés à intervalles réguliers, on utilise la transformée de Fourier. Le périodogramme est un moyen de checher des signaux périodiques dans des données échantillonnées irrégulièrement. On les notera 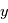 . Le périodogramme de Lomb-Scargle d'un signal
. Le périodogramme de Lomb-Scargle d'un signal 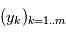 échantillonné aux instants
échantillonné aux instants 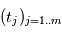 est défini comme suit pour une fréquence quelconque
est défini comme suit pour une fréquence quelconque 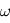 :
:
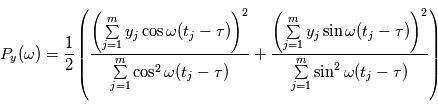 où
où 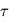 vérifie:
vérifie:
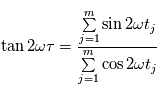
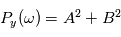 où
où 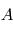 et
et 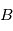 sont les paramètres minimisant
sont les paramètres minimisant 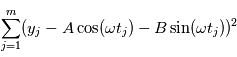 . Le modèle
. Le modèle 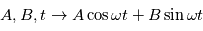 est linéaire en
est linéaire en 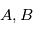 , on a donc une solution explicite à la minimisation.
, on a donc une solution explicite à la minimisation.
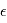 de variance unité,
de variance unité, 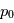 une valeur réelle fixée et
une valeur réelle fixée et 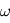 une fréquence quelconque, la probabilité que
une fréquence quelconque, la probabilité que 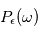 dépasse
dépasse 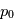 est
est 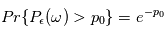 . En d'autres termes, la probabilité qu'une valeur du périodogramme à
. En d'autres termes, la probabilité qu'une valeur du périodogramme à 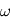 fixée soit "au moins aussi grand que
fixée soit "au moins aussi grand que 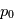 " par hasard décroît exponentiellement. Supposons que l'on ait un signal
" par hasard décroît exponentiellement. Supposons que l'on ait un signal 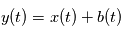 où
où 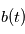 est un bruit gaussien de variance unité et nous trouvons un pic de taille
est un bruit gaussien de variance unité et nous trouvons un pic de taille 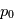 , on calcule la probabilité de trouver un pic au moins aussi grand si le signal n'est composé que de bruit:
, on calcule la probabilité de trouver un pic au moins aussi grand si le signal n'est composé que de bruit: 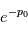 . Si cette valeur est petite, on pourra confirmer la détection d'un signal avec une erreur de fausse alarme de
. Si cette valeur est petite, on pourra confirmer la détection d'un signal avec une erreur de fausse alarme de 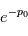 . Ce procédé n'est autre qu'un test de signification statistique.
. Ce procédé n'est autre qu'un test de signification statistique.
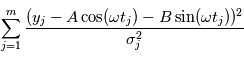 où
où 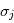 est la variance du bruit à la mesure
est la variance du bruit à la mesure 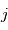 .
.
