| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Méthode des moindres carrés |
Pour des bruits gaussiens indépendants, maximiser la vraisemblance, revient à minimiser 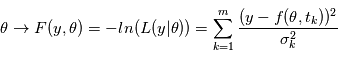 puisque
puisque 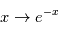 est une fonction décroissante. La méthode consistant à minimiser
est une fonction décroissante. La méthode consistant à minimiser 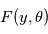 s'appelle la méthode des moindres carrés. C'est la méthode d'estimation de loin la plus utilisée dans tous les domaines. Elle est parfois utilisée quand les bruits ne sont pas gaussiens, mais il faut garder à l'esprit qu'elle n'a alors plus de propriétés statistiques sympathiques (sauf quand le modèle est linéaire en
s'appelle la méthode des moindres carrés. C'est la méthode d'estimation de loin la plus utilisée dans tous les domaines. Elle est parfois utilisée quand les bruits ne sont pas gaussiens, mais il faut garder à l'esprit qu'elle n'a alors plus de propriétés statistiques sympathiques (sauf quand le modèle est linéaire en  .
.
Dans notre cas, les paramètres 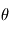 sont les éléments des orbites, les paramètres du bruit stellaire, du mouvement propre, etc. La fonction
sont les éléments des orbites, les paramètres du bruit stellaire, du mouvement propre, etc. La fonction 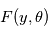 a donc de nombreux paramètres, et trouver son minimum global est une tâche ardue qui fait l'objet d'une littérature très vaste.
a donc de nombreux paramètres, et trouver son minimum global est une tâche ardue qui fait l'objet d'une littérature très vaste.
Lorsque le modèle est linéaire en 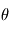 i. e.
i. e. 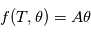 où
où 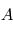 est une certaine matrice dépendant des instants d'observation
est une certaine matrice dépendant des instants d'observation 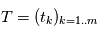 , l'ajustement est beaucoup plus simple car il a une solution explicite (voir mini-projet). On essaye de se ramener autant que possible à des ajustements linéaires. La plupart du temps, on estime les paramètre les uns après les autres, puis un ajustement global est réalisé. Une démarche classique consiste à:
, l'ajustement est beaucoup plus simple car il a une solution explicite (voir mini-projet). On essaye de se ramener autant que possible à des ajustements linéaires. La plupart du temps, on estime les paramètre les uns après les autres, puis un ajustement global est réalisé. Une démarche classique consiste à:
Sur la figure, on représente les étapes d'un ajustement d'un signal astrométrique simulé (2 planètes, 45 observations). De gauche à droite et de haut en bas:
 En vert signal après correction des bruits instrumentaux et atmosphériques
En vert signal après correction des bruits instrumentaux et atmosphériques  . Le mouvement propre (tendance linéaire) et la parallaxe (oscillation) dominent très nettement le signal.
. Le mouvement propre (tendance linéaire) et la parallaxe (oscillation) dominent très nettement le signal.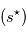 . En rouge: signal estimé
. En rouge: signal estimé 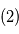 en soustrayant le mouvement propre, l'accélération de perspective et la parallaxe au signal
en soustrayant le mouvement propre, l'accélération de perspective et la parallaxe au signal 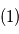 .
.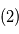 . En vert
. En vert 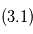 : orbite d'une planète ajustée sur
: orbite d'une planète ajustée sur 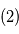 .
.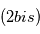 : signal
: signal 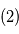 dont on a soustrait
dont on a soustrait 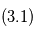 . En vert
. En vert 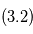 :orbite d'une planète ajustée sur
:orbite d'une planète ajustée sur 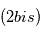 .
.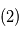 . En vert:
. En vert: 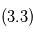 , ajustement de deux planètes en partant des estimations
, ajustement de deux planètes en partant des estimations 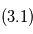 et
et 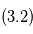 .
.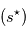 . On ajuste tous les paramètres simultanément sur
. On ajuste tous les paramètres simultanément sur  en partant des estimations précédentes. Le signal en rouge représente le signal planétaire de cet ajustement.
en partant des estimations précédentes. Le signal en rouge représente le signal planétaire de cet ajustement.