| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Périodogramme |
Evaluer les résidus sur une grille d'un modèle à 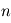 paramètres, où chacun d'eux peut prendre
paramètres, où chacun d'eux peut prendre 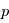 valeurs recquiert
valeurs recquiert 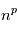 évaluations, ce qui devient rapidement ingérable numériquement. Les planètes ont un mouvement périodique, donc il est raisonnable de checher des signaux périodiques dans le signal en ne faisant varier que la période du signal recherché. Pour des signaux échantillonnés à intervalles réguliers, on utilise la transformée de Fourier. Le périodogramme est un moyen de checher des signaux périodiques dans des données échantillonnées irrégulièrement. On les notera
évaluations, ce qui devient rapidement ingérable numériquement. Les planètes ont un mouvement périodique, donc il est raisonnable de checher des signaux périodiques dans le signal en ne faisant varier que la période du signal recherché. Pour des signaux échantillonnés à intervalles réguliers, on utilise la transformée de Fourier. Le périodogramme est un moyen de checher des signaux périodiques dans des données échantillonnées irrégulièrement. On les notera 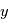 . Le périodogramme de Lomb-Scargle d'un signal
. Le périodogramme de Lomb-Scargle d'un signal 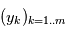 échantillonné aux instants
échantillonné aux instants 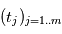 est défini comme suit pour une fréquence quelconque
est défini comme suit pour une fréquence quelconque  :
:
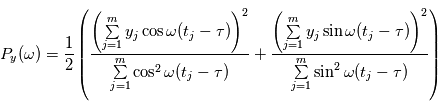 où
où 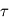 vérifie:
vérifie:
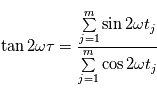
Cette expression est équivalente à 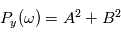 où
où 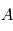 et
et 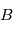 sont les paramètres minimisant
sont les paramètres minimisant 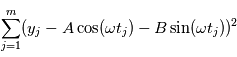 . Le modèle
. Le modèle 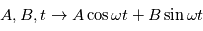 est linéaire en
est linéaire en 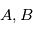 , on a donc une solution explicite à la minimisation.
, on a donc une solution explicite à la minimisation.
Le périodogramme a une propriété très intéressante: si le signal d'entrée est un bruit gaussien 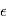 de variance unité,
de variance unité, 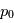 une valeur réelle fixée et
une valeur réelle fixée et 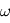 une fréquence quelconque, la probabilité que
une fréquence quelconque, la probabilité que 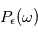 dépasse
dépasse 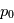 est
est 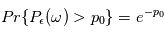 . En d'autres termes, la probabilité qu'une valeur du périodogramme à
. En d'autres termes, la probabilité qu'une valeur du périodogramme à 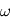 fixée soit "au moins aussi grand que
fixée soit "au moins aussi grand que 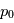 " par hasard décroît exponentiellement. Supposons que l'on ait un signal
" par hasard décroît exponentiellement. Supposons que l'on ait un signal 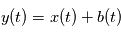 où
où 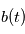 est un bruit gaussien de variance unité et nous trouvons un pic de taille
est un bruit gaussien de variance unité et nous trouvons un pic de taille 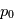 , on calcule la probabilité de trouver un pic au moins aussi grand si le signal n'est composé que de bruit:
, on calcule la probabilité de trouver un pic au moins aussi grand si le signal n'est composé que de bruit: 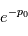 . Si cette valeur est petite, on pourra confirmer la détection d'un signal avec une erreur de fausse alarme de
. Si cette valeur est petite, on pourra confirmer la détection d'un signal avec une erreur de fausse alarme de 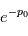 . Ce procédé n'est autre qu'un test de signification statistique.
. Ce procédé n'est autre qu'un test de signification statistique.
La figure montre un exemple de périodogramme. Il s'agit d'un périodogramme d'une des coordonnées d'un signal astrométrique simulé dont on a soustrait le mouvement propre et la parallaxe. En bleu, on représente un périodogramme idéal, sans bruit, avec 10000 observations. Le périodogramme représenté en rouge est lui calculé pour 45 observations. Le pic le plus haut correspond bien à une fréquence réelle. Par contre, le deuxième pic le plus important (à 0.37 rad/s) ne correspond pas à une sinusoïde. C'est ce qu'on appelle un alias de la fréquence principale.
En pratique, la variance du bruit n'est pas unitaire et dépend de l'instant de mesure. On peut corriger ce problème en minimisant un critère pondéré 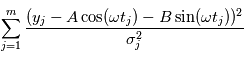 où
où 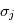 est la variance du bruit à la mesure
est la variance du bruit à la mesure 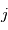 .
.