Traitement statistique

Rappelons qu'une variable aléatoire peut être vue comme un programme informatique qui délivre des valeurs suivant une certaine distribution de probabilité lorsqu'on lui demande. Le problème que nous posons maintenant est équivalent au suivant. Supposons qu'un ordinateur ait en mémoire des paramètres 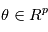$\theta \in \mathbb{R}^p$ (nombre de planètes, leurs caractéristiques orbitales, la période de rotation de l'étoile etc.). S'il n'y avait pas de bruit, une mesure à l'instant 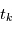t_k reviendrait à demander à l'ordinateur d'évaluer une fonction 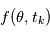$f(\theta,t_k)$ . Nous connaissons 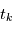t_k et 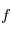(c'est l'un des modèles de la page précédente), mais nous ne connaissons pas 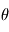$\theta$ . Notre but est de le déterminer à partir des mesures 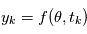$y_k = f (\theta,t_k)$ . Ce principe est similaire à la résolution d'une énigme: quelqu'un connaît une information 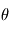$\theta$ et nous essayons de la deviner en posant une question. Dans le cas sans bruit, celui qui pose l'énigme ne nous induit pas en erreur, mais cela ne veut pas dire que la résolution est facile !

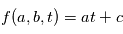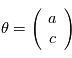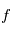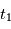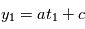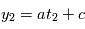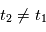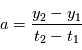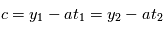Exemple: on veut trouver les paramètres d'une fonction affine du temps f(a,b,t) = at+c (ici $\theta = \left( \begin{array}{c} a \\c \end{array} \right)$ ). On évalue la valeur de en t_1 , on obtient y_1 = at_1+c : on a deux inconnues pour une équation, on ne peut pas résoudre. Si on a y_2 = at_2 + c , avec $t_2 \neq t_1$ , alors on a $a = \frac{y_2-y_1}{t_2-t_1}$ et c = y_1 - at_1 = y_2 - at_2 .

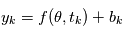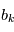Notre cas est plus compliqué. Les valeurs que nous obtenons sont $y_k = f(\theta, t_k) + b_k$ où b_k est la réalisation d'une variable aléatoire 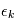$\epsilon_k$ . A l'appel numéro 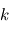du programme, l'ordinateur fait appel à un autre programme qui délivre une variable alétoire selon une certaine loi. En l'occurrence, nous supposons cette loi gaussienne. Si nous faisons 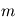mesures, tout se passe comme si un programme principal évaluait la fonction 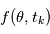$f(\theta, t_k)$ et 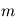programmes secondaires 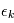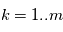$\epsilon_k$ , k=1..m retournent chacun une valeur 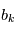b_k . Si nous pouvions remonter le temps et faire les mesures plusieurs fois aux mêmes instants, on aurait des des vecteurs de mesures 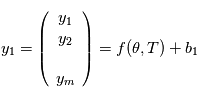$y_1 = \left( \begin{array}{c} y_1 \\y_2 \\ \\y_m \end{array} \right) = f(\theta,T) + b_1$ , puis 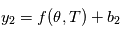$y_2 = f(\theta,T) + b_2$ etc. 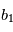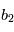(notez qu'ici b_1 et b_2 sont des vecteurs.

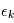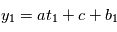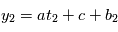Comme nous ne connaissons que la loi suivie par les variables $\epsilon_k$ , ils nous est impossible de connaître les paramètres avec certitude. On leur attache une "erreur", qui quantifie l'incertitude que l'on a sur eux. En reprenant l'exemple précédent on mesure y_1 = at_1 + c +b_1 et y_2 = at_2 + c +b_2 . Si on estime 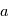et 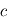avec les mêmes formules, on fera une erreur 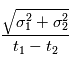$\frac{\sqrt{\sigma_1^2 + \sigma_2^2}}{t_1-t_2}$ sur 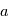et une erreur 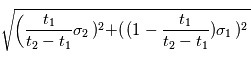$\sqrt{\left(\frac{t_1}{t_2-t_1} \sigma_2\left)^2 + \right((1-\frac{t_1}{t_2-t_1}) \sigma_1 \left)^2}$ sur 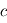(admis).