Loi du chi 2

Nous nous sommes toujours ramenés à des modèles du type: modèle déterministe + bruit gaussien. Afin de vérifier que les observations sont compatibles avec le modèle, on étudie les résidus, définis comme "les observation - le modèle ajusté".

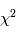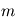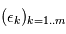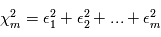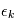La loi du $\chi^2$ est un outil commode pour étudier le comportement de plusieurs variables gaussiennes. Considérons d'abord une famille de variables aléatoires gaussiennes indépendantes $(\epsilon_k)_{k=1..m}$ , de moyenne nulle et de variance unité. On forme la quantité $\chi^2_m= \epsilon_1^2 + \epsilon_2^2 + ... + \epsilon_m^2$ . Comme les $\epsilon_k$ sont des variables aléatoires, les 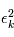$\epsilon_k^2$ le sont aussi. La somme de variables alétoires étant toujours une variable alétoire, 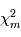$\chi^2_m$ suit une certaine loi de probabilité. Dans l'analogie avec un programme informatique, la variable alétoire 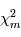$\chi^2_m$ se comporte comme un programme qui appelle 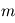programmes générant une variables gaussiennes, puis additionne leurs carrés. Elle est appelée loi du 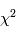$\chi^2$ à m degrés de liberté. On peut montrer qu'en moyenne une variable gaussienne au carré 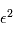$\epsilon^2$ a une moyenne de 1. En conséquence, 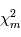$\chi^2_m$ vaudra typiquement .

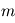Pourquoi cette loi serait utile pour notre cas ? Si le modèle est bien ajusté, les résidus doivent se comporter comme un bruit gaussien. En supposant que les erreurs sont toutes indépendantes, de moyenne nulle et de variance unité, les résidus 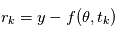$r_k = y-f(\theta,t_k})$ en sont une réalisation. Donc 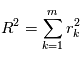$R^2=\sum\limits_{k=1}^m r_k^2$ est une réalisation d'une loi du 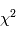$\chi^2$ à 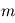degrés de liberté. Si 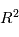R^2 est de l'ordre de 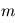, le modèle est cohérent. Sinon, le modèle ou les paramètres ajustés sont à revoir.

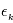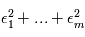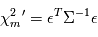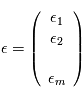En pratique, les erreurs $\epsilon__k$ ne sont évidemment pas de variance unité et parfois pas indépendantes. Par contre on peut à bon droit supposer qu'elles sont de moyenne nulle. 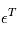Pour se ramener au cas précédent, on calcule non pas une réalisation de $\epsilon_1^2+...+\epsilon_m^2$ mais de $\chi^2_m'=\epsilon^T \Sigma^{-1} \epsilon$ où $\epsilon = \left( \begin{array}{c} \epsilon_1 \\ \epsilon_2 \\ \\ \epsilon_m \end{array} \right)$ , $\epsilon^T$ est sa transposée et 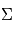$\Sigma$ est la matrice des variances-covariances de 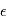$\epsilon$ . 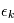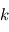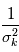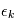Dans le cas où les $\epsilon_k$ sont indépendantes, la matrice des variances-covariances est diagonale, son -ème terme diagonal étant $\frac{1}{\sigma_k^2}$ , soit l'inverse de la variance de $\epsilon_k$ .