Signification statistique

Il esiste plusieurs outils pour s'assurer qu'une détection possible n'est pas due au bruit. L'un des plus utilisé est le test de signification (significance en anglais), qui consiste à calculer la probabilité d'avoir le signal observé "au moins aussi grand" s'il n'y avait en réalité que du bruit. Par exemple, qupposons que l'on veuille mesurer une quantité 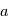qui est perturbée par un bruit gaussien additif 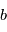de moyenne nulle et d'écart-type 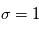$\sigma=1$ , donnant une mesure y = a+b .

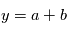Si il n'y avait en réalité pas de signal (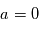 a=0 ), les mesures seraient uniquement dues au bruit. On imagine deux cas de figures:

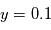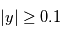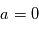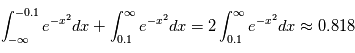
1er cas: on mesure . La probabilité d'avoir obtenue une valeur au moins aussi grande par hasard, c'est à dire la probabilité que $|y| \geq 0.1$ sachant que est $\int_{-\infty}^{-0.1} e^{-x^2}dx + \int_{0.1}^{\infty} e^{-x^2}dx = 2 \int_{0.1}^{\infty} e^{-x^2}dx \approx 0.818$
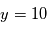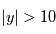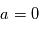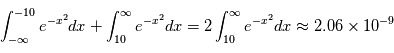
2ème cas: on mesure . La probabilité pour que alors que est $\int_{-\infty}^{-10} e^{-x^2}dx + \int_{10}^{\infty} e^{-x^2}dx = 2 \int_{10}^{\infty} e^{-x^2}dx \approx 2.06 \times 10^{-9}$

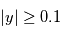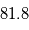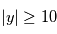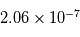Ces valeurs ont une interprétation: si on réalisait exactement le même type de mesure alors qu'il n'y a pas de signal, on observerait $|y| \geq 0.1$ dans 81.8 % des cas et $|y| \geq 10$ dans $2.06 \times 10^{-7}$ % des cas.Dans le premier cas, la probabilité d'avoir un signal aussi grand que celui que l'on a mesuré est grande. On ne peut pas assurer qu'un signal a été détecté. Par contre, dans le deuxième cas on serait dans un des deux cas sur un milliard où le signal serait dû au bruit. 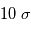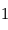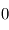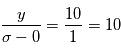On peut alors dire qu'on a détecté un signal à $10 \;\sigma$ , car la valeur de l'écart-type du bruit est , sa moyenne est , donc on a $\frac{y}{\sigma-0} = \frac{10}{1} = 10$ .

Détecter un signal "à 10 sigmas" est un luxe que l'on peut rarement se payer. Les détections sont annoncées plutôt pour des valeurs de 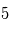sigmas.

Remarque importante: on calcule la probabilité d'avoir les observations sachant qu'il n'y a pas de signal et non la probabilité d'avoir un signal sachant les observations qui est une quantité qui a davantage de sens. Le calcul de cette dernière quantité se fait dans le cadre du calcul bayésien, outil très puissant qui ne sera pas développé dans ce cours.