Emission volumique

Pour chaque processus, on définit le taux de production de O dans l'état excité ¹S, c'est à dire le nombre d'atomes d'oxygène produit dans l'état ¹S par unité de volume et par unité de temps. Pour les deux premiers processus décrit à la page précédente, ce taux de production est proportionnel à la densité de CO₂. Pour le troisième processus il est proportionnel à la densité de O₂⁺ et pour le dernier processus il est proportionnel à la densité de O.

Le taux de production Q1 du premier processus est donné par:

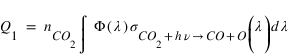
Φ(λ) étant le flux solaire à la longueur d'onde λ et σ_CO2+hν → _{CO+O(1S) )} la section efficace du processus considéré pour la longueur d’onde λ.

Le taux de production Q₂ du second processus est donné par

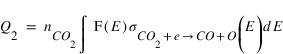
F(E) étant le flux de photoélectrons d'énegie E et σ_CO2+e→_{CO +O}(E) la section efficace de ce processus pour un életron d'énergie E

Le taux de production Q3 du troisième processus a une forme similaire à celle du processus 2

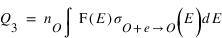
Le taux de production du Q₄ du quatrième processus peut s'écrire sous une forme identique à Q₂ et Q₃. Cependant, contrairement aux processus 2 et 3 qui nécessitent des électrons avec des énergies suffisante pour dissocier CO₂ ou exciter O. La recombinaison dissociative se fait principalement avec des électrons de basse énergie dont la distribution en énergie est bien décrite par une distribution maxwellienne. L'intégration peut alors être remplacée par une fonction ne dépendant que de la densité et de la température des électrons. Le terme Q4 peut alors s'écrire sous la forme

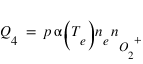
Le coefficient α est appelé coefficient de réaction et contient tout l'information de nature cinétique. Il dépend de la température des électrons, p est un nombre compris entre 0 et 1 qui représente la probabilité que l'état excité ¹S soit produit par la réaction (p ~ 4%).

L'atome dans l'état excité ¹S produit par un des quatre mécanismes ci-dessus peut se désexciter vers l'état ¹D ou l'état fondamental 3P. Seule la desexcitation vers l'état ³P conduit à l'émission d'un photon de longeur d'onde 297 nm. Les proportions de desexcitation de ¹S vers ³P et ¹S vers ¹D sont directement proportionnel aux coefficients d'Einstein des transitions notés A₂₉₇ et A_557.

L'émission volumique totale à 297 nm est donc donnée par

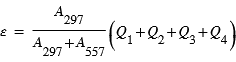
Dans ce calcul, on a négligé les processus de désexcitation par collisions (quenching). Ce terme peut être pris en compte en ajourant sa fréquence au dénominateur