Modèle de Bohr

Hypothèses du modèle de Bohr de l'hydrogène: Le modèle de Bohr de l'atome d'hydrogène a été élaboré en 1913 par Niels Bohr pour expliquer la structure en raies des spectres d'émissions des atomes. Ce modèle repose sur une description classique du mouvement de l'électron autour du noyau mais impose une quantification de son moment cinétique et suppose que l'électron ne rayonne pas sur une orbite stable circulaire.

Description du modèle:

L'électron est soumis à la force électrostatique radiale du noyau. Le mouvement se fait donc dans un plan. On note z l'axe perpendiculaire à ce plan. L'équation fondamentale de la dynamique, appliquée à l'électron de masse m_e en coordonnées cylindriques, projeté sur les axes r et θ s'écrit:

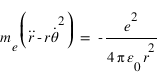
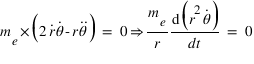
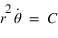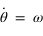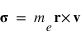La seconde équation s'intègre facilement et conduit à la loi des aires , comme la trajectoire est suppposée circulaire, la vitesse angulaire est constante. Le moment cinétique est définit par ou 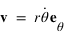est le vecteur vitesse. Le moment cinétique est donc une constante donnée par 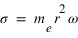L'équation fondamentale de la dynamique projetée sur l'axe r qui traduit l'équilibre entre la force électrostatique et la force centrifuge peut se réécrire sous la forme: 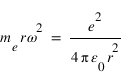Ce qui permet de déterminer la vitesse angulaire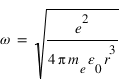

Par ailleurs, on suppose que le moment cinétique est quantifié, c'est à dire qu'il ne peut prendre que des valeurs multiples de 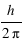: 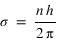. On en déduit l'expression des rayons des orbites stationnaires : 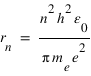L'énergie totale de l'électron sur l'orbite quantifiée est la somme de son énergie potentielle électrostatique et de son énergie cinétique : 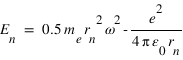En remplaçant r_n et ω par leur expression, on obtient les niveaux d'énergie quantifiés :

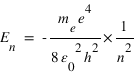
Limites du modèle de Bohr :

Le modèle de Bohr ne permet pas de décrire le spectre d'émission d'espèces polyélectroniques et la notion de trajectoire est incompatible avec le principe d'incertitude d'Heisenberg. Le modèle de Bohr sera finalement abandonné et remplacé par la théorie quantique dans les années 1920 dans la laquelle l'électron n'est plus décrit comme une particule ponctuelle mais par une fonction d'onde. La physique quantique ne sera pas décrite dans ce cours.