Diffusion résonante et diffusion fluorescente : Exemple émission Lyman-alpha de l'hydrogène atomique

L'hydrogène est l'espèce neutre majoritaire dans l'Univers. Toutes les planètes du système solaire contiennent de l'hydrogène sous forme atomique qui domine à hautes altitudes. Sur les planètes telluriques comme Vénus, la Terre et Mars, cet hydrogène est produit par la dissociation de la vapeur d'eau atmosphérique. A haute altitude, cet hydrogène peut diffuser le rayonnement solaire à 121.6 nm (UV) dans toutes les directions. L'intensité du flux diffusé est d'autant plus intense que le rayonnement solaire est intense, donc que la planète est proche du Soleil.

On défiinit le facteur d'excitation g_exc comme le nombre moyen de diffusions par seconde et par atome d'hydrogène. Lorsque le milieu est assez dilué, cette fréquence de diffusion est donnée par:

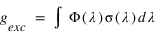
ou Φ(λ) est le flux solaire à la longueur d'onde λ (en photons/nm/s/m²) et σ(λ) la section efficace de diffusion d'un atome d'hydrogène à la longueur d'one λ (en m²). Le profil spectral de la section efficace n'est pas une fonction infiniment fine à 121.6 nm. Elle possède une certaine largeur spectrale qui peut résulter de différents mécanismes.

• Elargissement naturel : L'inégalité d'Heisenberg relie l'incertitude sur l'énergie d'un photon émis lors d'une transition d'un état excité vers un état de plus basse énergie et la durée de vie de cet état excité. La mesure de la longeur d'onde d'un photon émis lors d'une transition n'est donc jamais exactement la même.
• Elargissement par effet Doppler : La longueur d'onde d'un photon solaire est décalé vers le rouge ou vers le bleu selon que l'atome d'hydrogène s'éloigne ou s'approche du Soleil. Tous les atomes d'hydrogène n'ont pas exactement la même vitesse. La distribution des vitesses, dans un milieu à l'équilibre thermodynamique local a une forme gaussienne. La largeur de cette distribution dépend de la température du milieu. Elle est d'autant plus large que la température est élevée.
• Elargissment par collisions: Les collisions peuvent modifier légèrement l'énergie des états excités et donc la longueur d'onde d'une transition.

Si l'on néglige l'élargissement naturel de la raie et l'élargissement par collisions. La section efficace suit un profil et gaussien et peut s'écrire sous la forme:

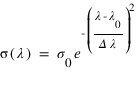
ou σ₀ est la section efficace au centre du profil, Δλ est la largeur Doppler du profil. Si par ailleurs on suppose que le flux solaire à un profil spectral "plat" : un profil spectral constant avec la longueur d'onde (Φ(λ) = Φ₀) au voisinage de 121.6 nm, le facteur d'excitation se calcule facilement et l'on obtient:

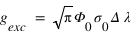
Le nombre de photons diffusés par unité de volume et de temps s'appelle le taux d'émission volumique, il est simplement donné par le produit entre le facteur d'excitation et la densité d'hydrogène (atome/cm³).

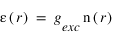
Ce taux volumique d'émission n'est en général pas mesurable directement, un instrument optique mesure seulement son intégrale sur une ligne de visée. On appelle intensité cette intégrale :

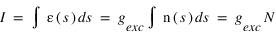
s est la coordonée curviligne le long de la ligne de visée. L'intégrale de la densité sur la ligne de visée, notée N est la colonne densité le long de la ligne de visée, elle s'exprime en général en atome/cm³. Cette grandeur est utile car c'est elle qui peut être directement déterminée par le rapport entre l'intensité mesurée et le facteur d'excitation généralement connu. L'intensité peut s'exprimer en photons/cm²/s. On préfère souvent utilisé une autre unité appelé Rayleigh, noté R définit par

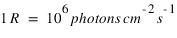
La diffusion résonante est le principal mécanisme produisant l'émission Lyman-alpha observée en UV autour des planètes. De nombreuses autres émissions sont produites par ce mécanisme comme par exemple la raie de l'oxygène atomique à 130.4 nm, la raie de l'ion O+ à 83.4 nm ou la raie du carbone atomique C à 156.5 nm. Dans le domaine visible on peut aussi citer la raie du sodium à 589 nm, dont la section efficace est suffisamment grande pour que cette émission soit observée dans des milieux extrêmement ténus comme les "atmosphères" de la Lune ou de Mercure.