Les événements possibles de sommes sont les nombres de 2 à 12. La preuve en est la liste exhaustive :
- (1, 1) = 2 ; 1 possibilité : Probabilité = 1/36 = 0.02777
- (1, 2) (2, 1) = 3 ; 2 possibilités : Probabilité = 2/36 = 1/18 = 0.05555
- (1, 3) (2, 2) (3, 1) = 4 ; 3 possibilités : Probabilité = 3/36 = 1/12 = 0.08333
- (1, 4) (2, 3) (3, 2) (4, 1) = 5 ; 4 possibilités : Probabilité = 4/36 = 1/9 = 0.11111
- (1, 5) (2, 4) (3, 3) (4, 2) (5, 1) = 6 ; 5 possibilités : Probabilité = 5/36 = 0.1388
- (1, 6) (2, 5) (3, 4) (4, 3) (5, 2) (6, 1) = 7 ; 6 possibilités : Probabilité = 6/36 = 1/6 = 0.16666
- (2, 6) (3, 5) (4, 6) (5, 3) (6, 2) =8 ; 5 possibilités : Probabilité = 5/36 = 0,13888
- (3, 6) (4, 5) (5, 4) (6, 3) = 9 ; 4 possibilités : Probabilité = 4/36 = 0,1111
- (4, 6) (5, 5) (6, 4) = 10 ; 3 possibilités : Probabilité = 3/36 = 0,083333
- (5, 6) (6, 5) = 11 ; 2 possibilités : Probabilité = 2/36 = 0.05555
- (6, 6) = 12 ; 1 possibilités : Probabilité = 1/36 = 0.027777
Cette liste donne les combinaisons pour toutes les sommes de deux dés. En utilisant la loi 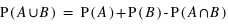 , il est alors possible de calculer la probabilité pour chaque valeur possible de la somme (de 2 à 12). Comme les évènements sont par nature disjoints l'un de l'autre,
, il est alors possible de calculer la probabilité pour chaque valeur possible de la somme (de 2 à 12). Comme les évènements sont par nature disjoints l'un de l'autre, 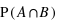 est toujours nulle. De ce fait, pour avoir la probabilité, il suffit de prendre le nombre total de combinaisons donnant la même valeur pour la somme, et de diviser ce nombre par 36.
est toujours nulle. De ce fait, pour avoir la probabilité, il suffit de prendre le nombre total de combinaisons donnant la même valeur pour la somme, et de diviser ce nombre par 36.
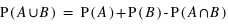 , il est alors possible de calculer la probabilité pour chaque valeur possible de la somme (de 2 à 12). Comme les évènements sont par nature disjoints l'un de l'autre,
, il est alors possible de calculer la probabilité pour chaque valeur possible de la somme (de 2 à 12). Comme les évènements sont par nature disjoints l'un de l'autre, 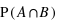 est toujours nulle. De ce fait, pour avoir la probabilité, il suffit de prendre le nombre total de combinaisons donnant la même valeur pour la somme, et de diviser ce nombre par 36.
est toujours nulle. De ce fait, pour avoir la probabilité, il suffit de prendre le nombre total de combinaisons donnant la même valeur pour la somme, et de diviser ce nombre par 36.