Se tester

Auteur: Gary Quinsac

Présentation des exercices
QCM sur la partie "découvrir"
Exercices : Représentation d'attitude
Exercices : Equations du mouvement
Exercice : Couples perturbateurs sur un CubeSat
Exercice : Propulsion
Exercices : Lois de commande

Présentation des exercices

Cette section doit vous permettre de vous exercer sur certaines des notions présentées dans ce cours. Un QCM reprend la première partie du cours, soit la découverte d'une mission spatiale, du standard CubeSat et du système de contrôle d'attitude et d'orbite. Des exercices plus poussés sont ensuite proposés, recouvrant la représentation d'attitude, les équations du mouvement, les couples perturbateurs et le contrôle d'attitude, la propulsion et enfin les lois de commande. La majeure partie des aspects abordés dans ce cours trouvent ainsi un écho dans ces exercices.

QCM sur la partie "découvrir"

Exercices : Représentation d'attitude

Auteur: Gary Quinsac

Matrice du Cosinus Directeur

Difficulté : ☆

On souhaite montrer que la MCD est une matrice orthonormale, c'est-à-dire que $[T] \ [T]^T = [I] = [T]^T \ [T]$ .

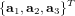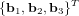Soit la MCD $[T]_{B|A}$ entre deux référentiels orthogonaux décrits par les vecteurs unitaires $\{ \bold a_1, \bold a_2, \bold a_3 \}^T$ et $\{ \bold b_1, \bold b_2, \bold b_3 \}^T$ :

$\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} = [T]_{B|A} \ \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}$

Question 1)

Ecrire le vecteur transposé de 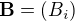$\bold B = (B_i)$ .

Question 2)

Calculer le produit 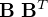$\bold B \ {\bold B}^T$ et conclure.

Auteur: Gary Quinsac

Angles d'Euler

Difficulté : ☆

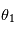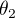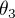Cet exercice a pour but de démontrer l'expression de la MCD à partir d'une certaine séquence d'angles d'Euler. On reprend la notation du cours en nommant $\theta_1$ , $\theta_2$ et $\theta_3$ les trois angles d'Euler.

Question 1)

Démontrer qu'en choisissant la séquence $[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3$ afin de passer du référentiel 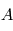au référentiel 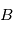, on obtient bien la formule présentée dans le cours :

$[T]_{B|A} = \begin{pmatrix} c_{\theta_2} c_{\theta_3} & c_{\theta_2} s_{\theta_3} & -s_{\theta_2} \\ s_{\theta_1} s_{\theta_2} c_{\theta_3} - c_{\theta_1} s_{\theta_3} & s_{\theta_1} s_{\theta_2} s_{\theta_3} + c_{\theta_1} c_{\theta_3} & s_{\theta_1} c_{\theta_2} \\ c_{\theta_1} s_{\theta_2} c_{\theta_3} +s_{\theta_1} s_{\theta_3} & c_{\theta_1} s_{\theta_2} s_{\theta_3} - s_{\theta_1} c_{\theta_3} & c_{\theta_1} c_{\theta_2} \end{pmatrix}$

Question 2)

Considérons maintenant la séquence suivante : $[T(\theta_1)]_1 \leftarrow [T(\theta_3)]_3 \leftarrow [T(\theta_2)]_2$ . Exprimer la MCD associée à cette séquence.

Auteur: Gary Quinsac inspiré de "Space Vehicle Dynamics and Control" de Bong Wie.

Quaternions

Difficulté : ☆

Considérons la séquence de rotations fixées par rapport à un satellite allant du référentiel 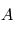au référentiel :

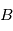$[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3$

Les quaternions associés à ces rotations sont :

$[T(\theta_1)]_1 = \begin{pmatrix} sin(\theta_1 / 2) \\ 0 \\ 0 \\ cos(\theta_1 / 2) \end{pmatrix}$ , $[T(\theta_1)]_1 = \begin{pmatrix} 0 \\ sin(\theta_2 / 2) \\ 0 \\ cos(\theta_2 / 2) \end{pmatrix}$ , $[T(\theta_1)]_1 = \begin{pmatrix} 0 \\ 0 \\ sin(\theta_3 / 2) \\ cos(\theta_3 / 2) \end{pmatrix}$

Question 1)

Montrer que les angles d'Euler de cette séquence de rotation sont reliés aux quaternions de la manière suivante :

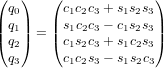
$\begin{pmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \end{pmatrix} = \begin{pmatrix} c_1 c_2 c_3 + s_1 s_2 s_3 \\ s_1 c_2 c_3 - c_1 s_2 s_3 \\ c_1 s_2 c_3 + s_1 c_2 s_3 \\ c_1 c_2 s_3 - s_1 s_2 c_3 \end{pmatrix}$

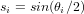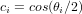
où $s_i = sin(\theta_i / 2)$ et $c_i = cos(\theta_i / 2)$

Question 2)

Vérifier que pour des angles infinitésimaux on obtient un quaternion très simple.

Exercices : Equations du mouvement

Auteur: Gary Quinsac

Cinématique d'attitude avec la MCD

Difficulté : ☆☆

On souhaite démontrer l'équation de la cinématique exprimée avec la MCD.

$\frac{d}{dt}([T]) = -[\Omega] \ [T]$ avec $[\Omega] = \begin{pmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{pmatrix}$ et $[T] = \begin{pmatrix} T_{11} & T_{12} & T_{13} \\ T_{21} & T_{22} & T_{23} \\ T_{31} & T_{32} & T_{33} \end{pmatrix}$

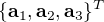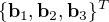Soit la MCD [T] entre deux référentiels orthogonaux décrits par les vecteurs unitaires $\{\bold{a}_1, \bold{a}_2, \bold{a}_3\}^T$ et $\{\bold{b}_1, \bold{b}_2, \bold{b}_3\}^T$ .

Question 1)

Rappeler la propriété principale de la MCD [T] .

Question 2)

Exprimer la dérivée de l'équation exprimant un vecteur du référentiel (B) en fonction d'un vecteur du référentiel (A).

Question 3)

Obtenir l'équation de la cinématique exprimée avec la MCD.

Question 4)

À partir de l'équation de la cinématique que nous venons de démontrer, exprimer les différentes coordonnées du vecteur vitesse angulaire.

Auteur: Gary Quinsac

Cinématique d'attitude avec les angles d'Euler

Difficulté : ☆☆

Cet exercice cherche à établir les équations de la cinématique pour certaines représentations d'Euler. Les premières questions considèrent la séquence d'Euler permettant de passer du référentiel (A) au référentiel (B) suivante : $[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3$ .

Question 1)

Ecrire les trois vecteurs vitesse angulaire correspondant à chaque transformation élémentaire en fonction des dérivées des angles d'Euler.

Question 2)

Exprimer le vecteur de vitesse angulaire 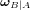${\boldsymbol\omega}_{B|A}$ en fonction des vecteurs de vitesse angulaire précédents.

Question 3)

Reformuler cette équation afin de faire apparaître les vecteurs de base des différents repères.

Question 4)

Exprimer les vecteurs de base des repères 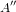A'' et 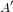en fonction de ceux de (B).

Question 5)

Montrer la relation de la cinématique pour cette séquence d'Euler :

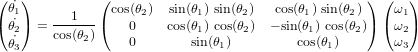
$\begin{pmatrix} \dot{\theta_1} \\ \dot{\theta_2} \\ \dot{\theta_3} \end{pmatrix} = \frac{1}{\textup{cos}(\theta_2)} \begin{pmatrix} \textup{cos}(\theta_2) & \textup{sin}(\theta_1) \ \textup{sin}(\theta_2) & \textup{cos}(\theta_1) \ \textup{sin}(\theta_2) \\ 0 & \textup{cos}(\theta_1) \ \textup{cos}(\theta_2) & -\textup{sin}(\theta_1) \ \textup{cos}(\theta_2) \\ 0 & \textup{sin}(\theta_1) & \textup{cos}(\theta_1) \end{pmatrix} \begin{pmatrix} \omega_1 \\ \omega_2 \\ \omega_3 \end{pmatrix}$

Question 6)

Considérons maintenant la séquence suivante : $[T(\theta_1)]_1 \leftarrow [T(\theta_3)]_3 \leftarrow [T(\theta_2)]_2$ . Exprimer alors l'équation de la cinématique.

Auteur: Gary Quinsac

Cinématique d'attitude avec les quaternions

Difficulté : ☆☆

Il est maintenant question de démontrer l'équation de la cinématique avec les quaternions.

Question 1)

Reprendre la forme de l'équation de la cinématique trouvée dans la dernière question du premier exercice sur les équations du mouvement :

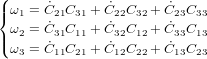
$\begin{cases} \omega_1 = \dot C_{21} C_{31} + \dot C_{22} C_{32} + \dot C_{23} C_{33} \\ \omega_2 = \dot C_{31} C_{11} + \dot C_{32} C_{12} + \dot C_{33} C_{13} \\ \omega_3 = \dot C_{11} C_{21} + \dot C_{12} C_{22} + \dot C_{13} C_{23} \end{cases}$

Substituer les coefficients de la MCD par leur forme avec les quaternons.

Question 2)

Exprimer la dérivée de l'équation contraignant les quaternions.

Question 3)

Regrouper ces 4 équations sous forme matricielle.

Question 4)

Utiliser une propriété remarquable de la matrice de quaternion obtenue dans la questions précédente pour exprimer la dérivée du quaternion.

Question 5)

Réécrire l'équation afin d'obtenir l'équation de la cinématique avec les quaternions.

Exercice : Couples perturbateurs sur un CubeSat

Auteur: Gary Quinsac

Couples perturbateurs agissant sur un CubeSat

Difficulté : ☆☆

Une mission scientifique nécessite l'envoie d'un CubeSat 3U sur une orbite circulaire à 300km d'altitude (ce qui correspond à une vitesse de 7726 m/s). On considère que le centre de masse de satellite se trouve décalé du centre géométrique de + [1; 1; 2] cm et que la surface du satellite est homogène. Étant donnée l'altitude, il est possible d'utiliser le champ magnétique pour effectuer le contrôle de l'attitude du CubeSat. Une combinaison de trois magnétocoupleurs, chacun étant orienté selon un axe du satellite, est proposée. Le courant maximum parcourant les bobines est ±0,2 A et le rayon du fil mesure 10,4 mm.

Voici différentes données nécessaires :

Données
Masse volumique de l'atmosphère à 300 km	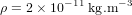$\rho = 2 \times 10^{-11} \ \textup{kg}.\textup{m}^{-3}$
Coefficient de trainée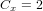
Constante gravitationnelle de la Terre	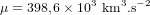$\mu = 398,6 \times 10^3 \ \textup{km}^{3} . \textup{s}^{-2}$
Rayon de la Terre	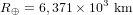$R_{\oplus} = 6,371 \times 10^3 \ \textup{km}$
Irradiance solaire moyenne	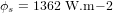$\phi_s = 1362 \ \textup{W}. \textup{m}{-2}$
Coefficient de réflexion moyen du satellite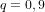
Champ magnétique terrestre à 300 km	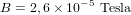$B = 2,6 \times 10^{-5} \ \textup{Tesla}$
Dipôle résiduel du satellite	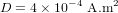$D = 4 \times 10^{-4} \ \textup{A} . \textup{m}^2$
Courant maximum dans magnéto-coupleurs	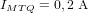$I_{MTQ} = 0,2 \ \textup{A}$
Diamètre de la bobine des magnéto-coupleurs	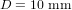$D = 10 \ \textup{mm}$

CubeSat 3U

CubeSat 3U de longueur l, de côtés a et b et de moments d'inertie I_xx, I_yy et I_zz.

Crédit : Gary Quinsac

Question 1)

Que signifie le fait que la surface du satellite est homogène ?

Question 2)

Estimer les dimensions et la masse totale du satellite.

Question 3)

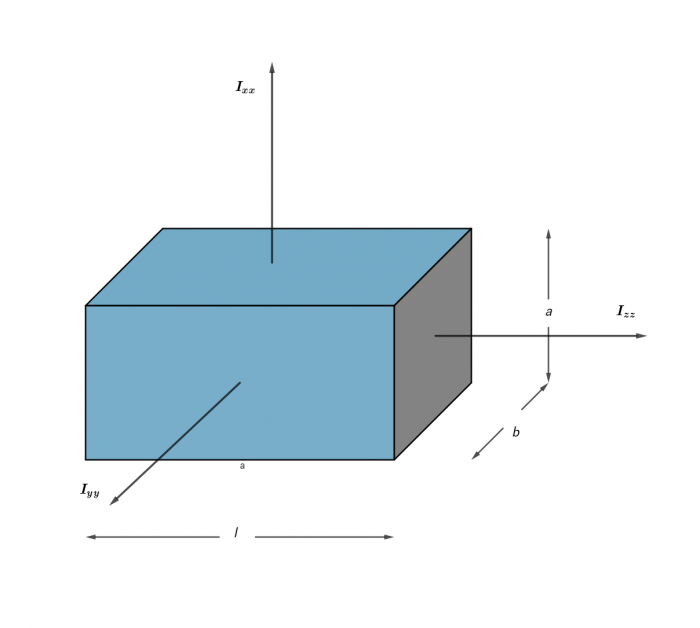
Quels sont les principaux moments d'inertie du satellite ?

Question 4)

Identifier les couples perturbateurs.

Question 5)

Exprimer les couples perturbateurs maximums créés par les différentes perturbations agissant sur le satellite si son axe +Y est aligné avec sa vitesse. On utilisera les notations données en introduction de l'exercice.

Question 6)

Estimer l'ordre de grandeur de la somme de tous les couples perturbateurs agissant sur le satellite.

Question 7)

Combien de spires la bobine du magnétocoupleur doit-elle contenir pour contrebalancer le couple perturbateur précédemment estimé ?

Exercice : Propulsion

Auteur: Gary Quinsac

Exercice

Difficulté : ☆

On reprend le CubeSat présenté lors de l'exercice précédent. Cette fois-ci, nous nous plaçons dans le cas où celui-ci doit effectuer une manœuvre orbitale nécessitant un incrément de vitesse de 50 m/s. Six systèmes de propulsion vous sont proposés, chacun étant défini par sa masse sèche M_sèche (masse du système de propulsion sans le carburant), son impulsion spécifique I_sp, sa force de poussée F et sa consommation électrique P.

Systèmes de propulsion
Type de propulsion	Modèle	M_sèche [kg]	I_sp [s]	F [N]	P [W]
Gaz froid	Palomar MiPS	0,89	50	3,5.10^-2	5
Mono-carburant	BGT-X5	1,24	220	5.10^-1	20
Bi-carburant	PM200	1,10	285	5.10^-1	6
Électromagnétique	PPTCUP	0,28	670	4.10^-5	2
Électrostatique	IFM Nano	0,64	3800	3,5.10^-4	32

Question 1)

Quel lien peut-on faire entre la vitesse d'expulsion du carburant l'impulsion spécifique I_sp ?

Question 2)

Estimer la quantité de carburant nécessaire pour effectuer la manœuvre souhaitée avec chacun des systèmes de propulsion.

Question 3)

Sachant que l'on cherche généralement à éviter d'allouer plus de 33% de la masse d'un satellite au système de propulsion

Question 4)

La puissance électrique disponible à bord d'un CubeSat 3U recouvert de panneaux solaires en orbite autour de la Terre est estimée à 7 W. Qu'est-ce que cela change au niveau de vos choix ?

Question 5)

En supposant que l'efficacité de la manœuvre ne dépend pas du lieu où celle-ci est effectuée, c'est à dire du moment, combien durerait-elle pour chacun des systèmes de propulsion proposés ? Cette hypothèse est fausse dans de nombreux cas, notamment lorsque les forces de poussée en jeu sont faibles et les manœuvres importantes (ce qui est le cas ici).

Exercices : Lois de commande

Auteur: Gary Quinsac

Étude d'un ressort

Difficulté : ☆

Cet exercice a pour but de vous entraîner à utiliser les transformations de Laplace pour résoudre une équation différentielle.

Considérons une masse m accrochée à un ressort de constante de rappel K. On mesure le déplacement vertical de la masse, provoqué par une stimulation u(t), par la grandeur x. L'installation est illustrée par cette figure.

Ressort

Crédit : Gary Quinsac

Question 1)

Quelle est l'équation de déplacement de la masse ?

Question 2)

On veut étudier le cas d'une stimulation impulsionnelle. Que devient u(t) ?

Question 3)

Exprimer la fonction de transfert du système.

Question 4)

Effectuer la transformée de Laplace inverse de la fonction de transfert afin d'exprimer le déplacement issu d'une stimulation impulsionnelle dans le domaine temporel.

Question 5)

Supposons maintenant que la stimulation n'est plus impulsionnelle mais une rampe 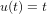u(t) =t . Afin d'obtenir la réponse dans le domaine temporel, il faudrait faire le produit de convolution de cette rampe avec la réponse impulsionnelle :

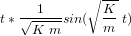
$t \ast \frac{1}{\sqrt{K \ m}} sin(\sqrt{\frac{K}{m}} \ t)$

Passer par la transformée de Foutier.

Auteur: Gary Quinsac

Représentation de la boucle de contrôle d'attitude

Nous allons retrouver la fonction de transfert de la boucle de contrôle d'attitude :

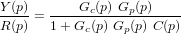
$\frac{Y(p)}{R(p)} = \frac{G_c(p) \ G_p(p)}{1+G_c(p) \ G_p(p) \ C(p)}$

On note R(p) le signal de référence, Y(p) le signal de sortie, D(p) la perturbation, U(p) le signal de contrôle, G_c(p) le contrôleur, E(p) l'erreur, G_p(p) le matériel à contrôler et C(p) la dynamique des capteurs.

Question 1)

Exprimer le signal de sortie en fonction du signal de contrôle.

Question 2)

Sachant que l'on considère que les perturbations sont nulles, exprimer le signal de contrôle en fonction de l'erreur.

Question 3)

Appliquer la même approche pour trouver l'expression de l'erreur.

Question 4)

Réorganiser les résultats précédents afin de retrouver l'expression de la fonction de transfert.

Réponses aux QCM

pages_nanosats-setester/qcm-partie-decouvrir.html

QCM 'Découvrir'

Question 1
Aide :
Acronyme anglais.

Solution : réponse 3) ( C'est une orbite basse ou "Low Earth Orbit" )
Question 2
Aide :
Les satellites sont habituellement classés en fonction de leur masse.

Solution : réponse 2) ( Cette catégorie concerne les satellites de 1 kg à 10 kg. Jusqu'à 6U un CubeSat doit peser moins de 10 kg. )
Question 3
Aide :
La construction intervient tardivement dans les phases de réalisation d'un projet spatial.

Solution : réponse 5) ( La construction et les tests ont lieu lors de cette phase. )
Question 4
Aide :
Tous ces avantages découlent de la standardisation des interfaces.

Solution : réponse 1) ( De nombreux sous-système "sur étagère" existant, il n'est plus nécessaire de développer entièrement son satellite. )
Solution : réponse 3) ( Il a permis le développement de déployeurs standardisés qualifiés pour bon nombre de lanceurs. )
Question 5
Aide :
Le segment spatial se constitue de la plateforme et de la charge utile.

Solution : réponse 1) ( Elle sert à échanger des données avec le sol. )
Solution : réponse 2) ( Vous devez avoir une idée assez précise de son utilité après ce cours. )
Solution : réponse 4) ( Elle assure, notamment, l'intégrité du satellite. )
Question 6
Aide :
Cette absoprtion par l'atmosphère est l'une des raisons d'être des premiers observatoires spatiaux.

Solution : réponse 1) ( Heureusement pour nous ! )
Solution : réponse 3)
Question 7
Solution : réponse 3)
Question 8
Solution : réponse 1) ( L'importance croissance des CubeSats commerciaux symbolise l'adoption de ce standard et encourage les nouveaux investisseurs. )
Question 9
Aide :
Le contrôle d'attitude concerne l'orientation du satellite dans l'espace.

Solution : réponse 2)
Question 10
Solution : réponse 3) ( C'est le système de guidage, navigation et contrôle. )

Réponses aux exercices

pages_nanosats/exercice-representation-attitude.html

Exercice 'Angles d'Euler'

Question 1
Aide :
Exprimer les trois rotations élémentaires telles que présentées dans le cours.

Aide :
Exprimer la matrice issue de la combinaison des rotations suivantes :

$\begin{cases} \begin{pmatrix} \bold a_1' \\ \bold a_2' \\ \bold a_3' \end{pmatrix} = [T(\theta_3)]_3 \ \begin{pmatrix} \bold a_1 \\ \bold a_2 \\ \bold a_3 \end{pmatrix} \\ \begin{pmatrix} \bold a_1'' \\ \bold a_2'' \\ \bold a_3'' \end{pmatrix} = [T(\theta_2)]_2 \ \begin{pmatrix} \bold a_1' \\ \bold a_2' \\ \bold a_3' \end{pmatrix} \\ \begin{pmatrix} \bold b_1 \\ \bold b_2 \\ \bold b_3 \end{pmatrix} = [T(\theta_1)]_1 \ \begin{pmatrix} \bold a_1'' \\ \bold a_2'' \\ \bold a_3'' \end{pmatrix} \end{cases}$
Question 2
Aide :
Suivre les mêmes étapes que pour la question précédente.

pages_nanosats/exercice-representation-attitude.html

Exercice 'Quaternions'

Question 1
Aide :
Utiliser le cours sur les séquences de rotations exprimées en termes de quaternion et la multiplication des quaternions.
Question 2
Aide :
Effectuer le développement limité de du quaternion obtenu précédemment.

pages_nanosats/exercice-equations-mouvement.html

Exercice 'Cinématique d'attitude avec la MCD'

Question 1
Aide :
Voir le cours où l'exercice sur la représentation d'attitude avec la MCD.
Question 2
Aide :
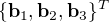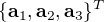Exprimer la relation de passage du vecteur $\{\bold{b}_1, \bold{b}_2, \bold{b}_3\}^T$ au vecteur $\{\bold{a}_1, \bold{a}_2, \bold{a}_3\}^T$ .

$\begin{pmatrix} \bold a_1 \\ \bold a_2 \\ \bold a_3 \end{pmatrix} = [T]^T \begin{pmatrix} \bold b_1 \\ \bold b_2 \\ \bold b_3 \end{pmatrix}$

Aide :
Prendre la dérivée de l'équation précédente.
Question 3
Aide :
Exprimer le vecteur de vitesse angulaire de 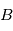par rapport à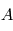 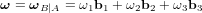${\boldsymbol\omega} = {\boldsymbol\omega}_{B|A} = \omega_1 {\bold b}_1 + \omega_2 {\bold b}_2 + \omega_3 {\bold b}_3$ et l'insérer dans l'équation précédente.

$\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} = \dot {[T]}^T \ \begin{pmatrix} \bold b_1 \\ \bold b_2 \\ \bold b_3 \end{pmatrix} + [T]^T \ \begin{pmatrix} \boldsymbol\omega \wedge \bold b_1 \\ \boldsymbol\omega \wedge \bold b_2 \\ \boldsymbol\omega \wedge \bold b_3 \end{pmatrix}$

Aide :
Remplacer par la matrice antisymétrique :

$[\Omega] = \begin{pmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{pmatrix}$
Question 4
Aide :
Il s'exprime en fonction des différents éléments de la MCD et de sa dérivée.

pages_nanosats/exercice-equations-mouvement.html

Exercice 'Cinématique d'attitude avec les angles d'Euler'

Question 1
Aide :
Penser à introduire les référentiels intermédiaires.
Question 2
Question 3
Question 4
Question 5
Question 6
Aide :
Suivez les mêmes étapes que pour la question précédente.

pages_nanosats/exercice-equations-mouvement.html

Exercice 'Cinématique d'attitude avec les quaternions'

Question 1
Aide :
$[T] = [T(\bold q)] = \begin{pmatrix} 1-2(q_2^2+q_3^2) & 2(q_1q_2+q_3q_0) & 2(q_1 q_3 - q_2 q_0) \\ 2(q_2q_1-q_3q_0) & 1-2(q_1^2+q_3^2) & 2(q_2q_3+q_1q_0) \\ 2(q_3q_1+q_2q_0) & 2(q_3q_2-q_1q_0) & 1-2(q_1^2+q_2^2) \end{pmatrix}$
Question 2
Aide :
Equation contraignant les quaternions : 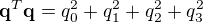$\bold{q}^T \bold{q} = q_0^2+q_1^2+q_2^2+q_3^2$
Question 3
Question 4
Aide :
La matrice de quaternion obtenue est orthonormale.
Question 5

pages_nanosats/exercice-couples-perturbateurs.html

Exercice 'Couples perturbateurs agissant sur un CubeSat'

Question 1
Question 2
Aide :
C'est un CubeSat 3U et on sait qu'une unité représente un cube de 10 cm d'arête et de 1,3 kg.
Question 3
Aide :
Comme première approximation, on peut considérer que le satellite est homogène et que son centre de masse se trouve parfaitement localisé en son centre. Les moments d'inertie principaux peuvent donc s'exprimer :
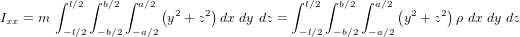
- $I_{xx} = m \ \int_{-l/2}^{l/2}{ \int_{-b/2}^{b/2}{ \int_{-a/2}^{a/2}{ \left( y^2 + z^2 \right) dx \ dy \ dz } } } = \int_{-l/2}^{l/2}{ \int_{-b/2}^{b/2}{ \int_{-a/2}^{a/2}{ \left( y^2 + z^2 \right) \rho \ dx \ dy \ dz } } }$
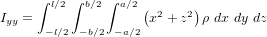
- $I_{yy} = \int_{-l/2}^{l/2}{ \int_{-b/2}^{b/2}{ \int_{-a/2}^{a/2}{ \left( x^2 + z^2 \right) \rho \ dx \ dy \ dz } } }$
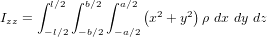
- $I_{zz} = \int_{-l/2}^{l/2}{ \int_{-b/2}^{b/2}{ \int_{-a/2}^{a/2}{ \left( x^2 + y^2 \right) \rho \ dx \ dy \ dz } } }$
Question 4
Aide :
Ils sont au nombre de 4.
Question 5
Aide :
Pour la trainée atmosphérique :
- Déterminer l'aire projetée le long de la direction du mouvement.
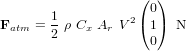
- Exprimer la force de trainée atmosphérique : $\bold F_{atm} = \frac{1}{2} \ \rho \ C_x \ A_r \ V^2 \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \ \textup{N}$
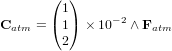
- Utiliser la position du centre de masse pour calculer les couples de trainée atmosphérique selon les trois axes principaux du satellite : $\bold C_{atm} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} \times 10^{-2} \wedge \bold F_{atm}$
Aide :
Pour le gradient de gravité :
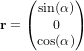- L'axe +Y étant parallèle à la vitesse du satellite et la trajectoire étant circulaire, le rayon vecteur de la force de gravitation se décompose dans le plan X-Z $\bold r = \begin{pmatrix} \textup{sin} (\alpha) \\ 0 \\ \textup{cos} (\alpha) \end{pmatrix}$ .
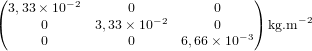
- La matrice d'inertie s'exprime : $\begin{pmatrix} 3,33 \times 10^{-2} & 0 & 0 \\ 0 & 3,33 \times 10^{-2} & 0 \\ 0 & 0 & 6,66 \times 10^{-3} \end{pmatrix} \textup{kg}.\textup{m}^{-2}$
- Appliquer la formule vue dans le cours : $\bold C_{GG} = \frac{3 \ \mu}{r^3} \bold r \wedge \left([I] \bold r \right)$
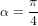- En exprimant le produit vectoriel, on se rend compte que le maximum correspond à $\alpha = \frac{\pi}{4}$ .
Aide :
Pour la pression solaire :
- Consider l'un des pires cas, c'est à dire que les faces +X ou +Y sont parfaitement orientées vers le Soleil, et en déduire la surface exposée et l'angle d'incidence.
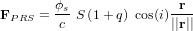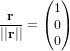- Exprimer la force de pression de radiation solaire : $\bold F_{PRS} = \frac{\phi_s}{c} \ S \left (1+q \right) \ \textup{cos}(i) \frac{\bold r}{||\bold r||}$ avec $\frac{\bold r}{||\bold r||} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$ et .
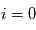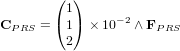
- Utiliser la position du centre de masse pour exprimer les couples de pression de radiation solaire selon les trois axes principaux du satellite : $\bold C_{PRS} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} \times 10^{-2} \wedge \bold F_{PRS}$
Aide :
Pour le gradient magnétique :
- Identifier le pire alignement entre le satellite et le champ magnétique terrestre : lorsque le dipôle résiduel et le champ magnétique sont perpendiculaires.
- Le couple correspondant est simplement le produit de ces deux valeurs : $C_m = D \ B$
Question 6
Question 7
Aide :
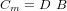
Les magnéto-coupleurs doivent pouvoir compenser tous les couples perturbateurs agissant sur le satellite. Ils doivent donc au moins fournir 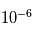$10^{-6}$ N.m.

Aide :
Rappelons les équations permettant de calculer le couple magnétique et le moment dipolaire :

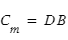et 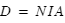, où N est le nombre de spire de la bobine.

pages_nanosats/exercice-propulsion.html

Exercice

Question 1
Aide :
Cette relation s'obtient facilement à partir de la relation exprimant la force en fonction de la vitesse d'expulsion et la définition de l'impulsion spécifique.
Question 2
Aide :
Le CubeSat faisant 3 unités, on peut estimer que sa masse totale est de 4 kg.
Question 3
Aide :
Il faut sommer la masse de carburant et la masse sèche afin d'obtenir la masse du système de propulsion dans son ensemble. Ceci n'est qu'une première approximation, notamment car on ne prend pas en compte la masse supplémentaire correspondant à des réservoirs plus gros.
Question 4
Question 5
Aide :
Dans ce cas, la durée de la manœuvre est directement liée à la force de poussée.

pages_nanosats/exercice-lois-de-commande.html

Exercice 'Étude d'un ressort'

Question 1
Question 2
Question 3
Aide :
Il faut prendre la transformée de Laplace de l'équation exprimée précédemment.

Aide :
Les conditions initiale sont supposées nulles.
Question 4
Question 5
Aide :
C'est une simple multiplication.