 Séparation spectrale des raies Lyman-alpha de l'hydrogène et du deutérium
Séparation spectrale des raies Lyman-alpha de l'hydrogène et du deutérium
Difficulté : ☆☆☆
Temps : 30 minutes
Dans le modèle de Bohr présenté dans le cours, on a supposé que le proton était immobile, on suppose maintentant que le proton n’est pas immobile.
Question 1)
Montrer que le référentiel barycentrique du système est galiléen.
Solution
L'équation de la dynamique de l'électron s'écrit:
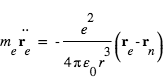
L'équation de la dynamique du noyau s'écrit:
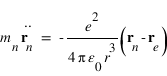
La somme de ces deux équations donne
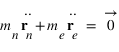
Par définition la position du barycentre du système est donnée par:
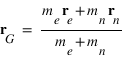
On en déduit que 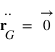
Le référentiel associé au barycentre est donc en mouvement uniforme par rapport au référentiel du laboratoire supposé galiléen. Le référentiel associé au barycentre est donc un référentiel galiléen.
Question 2)
On posera 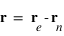 , où
, où 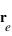 est la position de l'électron et
est la position de l'électron et 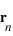 la position du noyau dans le référentiel du laboratoire, exprimer les positions de l'électron
la position du noyau dans le référentiel du laboratoire, exprimer les positions de l'électron 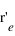 et du noyau
et du noyau 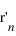 dans le référentiel barycentrique du système en fonction de
dans le référentiel barycentrique du système en fonction de 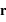
Solution
La position de l'électron dans le référentiel barycentrique est donnée par :
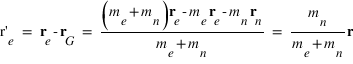
La position du noyau dans le référentiel barycentrique est donnée par :
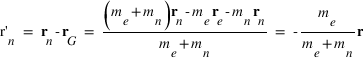
Question 3)
Réécrire l’équation de la dynamique pour l’électron et le proton dans le référentiel barycentrique et montrer que l'équation se réduit à la dynamique d'une particule de masse réduite μ que l'on exprimera en fonction de la masse de l'électron et du noyau.
Solution
Les équations de la dynamique de l'électron et du noyau dans le référentiel barycentrique s'écrivent:
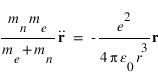
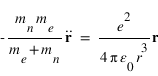
Il s'agit de deux fois la même équation de la dynamique d'une particule fictive de masse
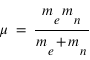 et de position
et de position 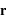
Question 4)
On suppose que la trajectoire de cette particule réduite est circulaire, déterminer la vitesse angulaire de la particule réduite. On suppose que le moment cinétique de cette particule réduite est quantifié et ne peut prendre que des valeurs du type 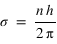 . déterminer les valeurs possibles de r et l'énergie de la particule en fonction de n.
. déterminer les valeurs possibles de r et l'énergie de la particule en fonction de n.
Solution
La résolution de l'équation est identique à celle effectuée dans le cours en remplaçant me par μ. La force étant radiale, la trajectoire de la particule réduite est plane. En coordonnées cylindriques, les équations projetées sur les axes 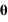 et
et 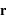 s'écrivent:
s'écrivent:
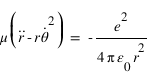
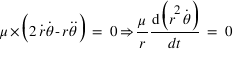
La deuxième équation conduit à
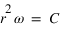
Comme on suppose que la trajectoire de la particule est circulaire
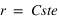
La première équation permet de déterminer la vitesse angulaire de la particule :
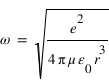
En utilisant la condition de quantification du moment cinétique, on obtient les valeurs de r et de l'énergie de la particule en fonction du nombre quantique n:
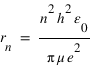
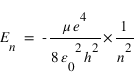
Question 5)
Calculer la longueur d’onde du photon émis lors de la transition du niveau m vers le niveau n de l’hydrogène et du deutérium atomique sachant que le noyau du deutérium est composé d'un proton et d'un neutron, on supposera que la masse d'un neutron est égale à la masse d'un proton.
Solution
En remplaçant μ par son expression avec mn = mp pour l'hydrogène et mn= 2mp pour le deutérium, on obtient:
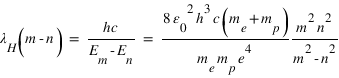
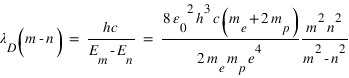
Question 6)
La masse du proton est 1.672622x10-27 kg et la masse d'un électron de 9.109383x10-31 kg. En déduire la longueur d'onde des transitions Lyman-alpha de l'hydrogène et du deutérium et en deduire le pouvoir de résolution nécessaire pour séparer spectralement les deux raies.
AideSolution
Prendre des valeurs des constantes les plus précises possibles pour l'application numérique.
L'émission Lyman-alpha correspond à la transition m = 2 vers n =1. L'application numérique donne λH = 121.568 nm et λD = 121.535 nm
Le pouvoir de résolution nécessaire pour séparer spectralement les deux raies est donc R = λ/dλ ≈ 3700.
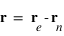 , où
, où 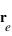 est la position de l'électron et
est la position de l'électron et 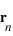 la position du noyau dans le référentiel du laboratoire, exprimer les positions de l'électron
la position du noyau dans le référentiel du laboratoire, exprimer les positions de l'électron 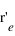 et du noyau
et du noyau 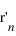 dans le référentiel barycentrique du système en fonction de
dans le référentiel barycentrique du système en fonction de 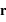
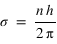 . déterminer les valeurs possibles de r et l'énergie de la particule en fonction de n.
. déterminer les valeurs possibles de r et l'énergie de la particule en fonction de n.