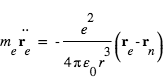
L'équation de la dynamique de l'électron s'écrit:
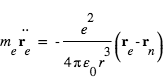
L'équation de la dynamique du noyau s'écrit:
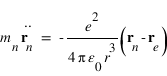
La somme de ces deux équations donne
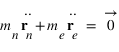
Par définition la position du barycentre du système est donnée par:
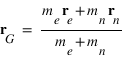
On en déduit que 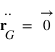
Le référentiel associé au barycentre est donc en mouvement uniforme par rapport au référentiel du laboratoire supposé galiléen. Le référentiel associé au barycentre est donc un référentiel galiléen.