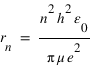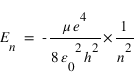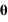 et
et 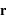 s'écrivent:
s'écrivent:
La résolution de l'équation est identique à celle effectuée dans le cours en remplaçant me par μ. La force étant radiale, la trajectoire de la particule réduite est plane. En coordonnées cylindriques, les équations projetées sur les axes 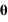 et
et 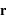 s'écrivent:
s'écrivent:
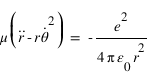
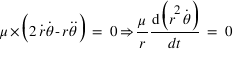
La deuxième équation conduit à
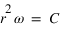
Comme on suppose que la trajectoire de la particule est circulaire
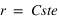
La première équation permet de déterminer la vitesse angulaire de la particule :
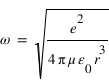
En utilisant la condition de quantification du moment cinétique, on obtient les valeurs de r et de l'énergie de la particule en fonction du nombre quantique n: