Vitesses radiales

Lorsque la distance entre une source d'onde et un observateur varie dans le temps, la longueur d'onde vue par l'observateur varie aussi. Ce phénomène, appelé effet doppler, est ce qui permet la détection du mouvement radial de l'étoile. Cet effet est géométrique, et présent pour tous les types d'ondes. Un exemple bien connu est celui de la sirène d'ambulance: le son qu'elle émet a l'air plus grave une fois qu'elle est passée devant nous. Pour le comprendre, considérons une personne qui se baigne sur une plage (suffisament loin pour que les vagues se brisent derrière elle). Si elle reste statique les vagues vont l'atteindre avec une certaine période. Selon qu'elle s'avance vers le large ou revient vers la plage elle rencontrera les vagues plus fréquemment ou moins fréquemment. De la même manière, plus vite l'étoile s'avance vers la Terre, plus la lumière reçue est décalée vers les hautes fréquences.

L'énergie par longueur d'onde d'une source lumineuse, ou de manière équivalente, le nombre de photons reçus par longueur d'onde, est appelé le spectre de cette source. Cette définition fait intervenir une mesure, le spectre dépend donc de l'observateur. La lumière provenant d'une étoile est composée à priori d'une infinité de longueurs d'ondes. Certaines d'entre elles sont absorbées par l'atmosphère de l'étoile, de sorte qu'elles sont absentes du spectre mesuré. On parle de raies d'absorption. Le spectre d'une étoile a un aspect proche de la figure 1. Si la source lumineuse et l'observateur sont immobiles l'un par rapport à l'autre, l'observateur verra un certain profil spectral 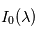(intensité par longueur d'onde 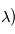. 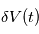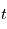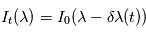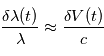Si maintenant la source et l'observateur ont une vitesse relative au temps , l'observateur verra un spectre décalé avec où 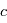est la vitesse de la lumière, dans l'hypothèse où 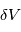est très petit par rapport à 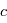. En mesurant 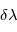on peut remonter à 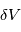. La présence d'une planète autour d'une étoile engendre un mouvement périodique de celle-ci, donc un décalage périodique du spectre (voir figure 2).

La mesure du décalage du spectre est utilisée depuis la fin du XIXe siècle pour détecter des étoiles binaires. La vitesse de l'étoile dont on observe le spectre (étoile cible) diminue avec le rapport de masse du compagnon et de l'étoile cible. Plus faible est la masse du compagnon plus il est difficile de le détecter. Les techniques ont été perfectionnées pour détecter des compagnons de masses de plus en plus faible.

Remarque: Une des limitations des mesures de vitesse radiale est qu'on ne mesure qu'une masse minimale car on mesure la projection du mouvement selon une direction. En notant 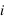l'angle entre la ligne de visée et le plan orbital d'un objet de masse 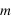, on mesure .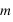

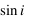En 1989, Latham trouve un objet d'une masse minimale de 11 masses de Jupiter (notée 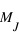) en orbite autour d'une étoile de type solaire. Etant donné que la limite admise à la masse d'une planète (au delà de laquelle le deutérium entre en fusion) est de 13 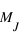, la conclusion de l'article est encore valide: il est possible que ce compagnon soit une Naine brune ou une super Jupiter, selon la valeur de 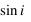. La première planète confirmée comme telle est découverte en 1995 par Michel Mayor et Didier Queloz à l'observatoire de Haute Provence.

Pour donner une idée des ordres de grandeur considérées, la Terre engendre un déplacement du Soleil d'environ 9 cm/s, Jupiter de 12.5 m/s. Un déplacement d'1 m par seconde correspond à un décalage relatif de longueurs d'onde 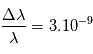. La précision attendue doit être maintenue sur plusieurs mois, voire plusieurs années.