La problématique de la détection par vitesse radiale et astrométrie est la suivante: quelles sont les orbites et les masses des planètes compagnons de l'étoile cible ? Comme les mesures sont entachées de bruit, on ne peut pas donner des paramètres orbitaux exacts. On estime aussi la "confiance" dans les valeurs des paramètres, souvent donnée sous forme de probabilités. On est aussi amené à se demander si toutes les planètes ont été détectées, et si les détections annoncées sont vraisemblables. En particulier, on étudie la stabilité du système trouvé.
La détection de planètes extrasolaires, comme d'autres problématiques de détection peut être subdivisé comme suit:
- Le problème direct, ou modélisation,Notre problème est bien plus complexe que celui de la page précédente. On ne cherche pas à estimer un paramère
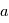à partir d'une mesure 
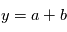, mais un vecteur de paramètre 
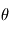à partir de plusieurs mesures aux instants 
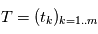, et les mesures dépendent de ces paramètres et des instants d'observations par une fonction 
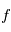: on a 
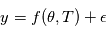, où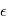 
est une variable aléatoire suivant une certaine loi de probabilité qui modélise l'incertitude. Le problème direct est la construction de la fonction 
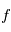. En l'occurrence, on utilise les équations bien connues de la mécanique céleste. "Si des planètes avec des paramètres orbitaux connus orbitent autour d'une étoile de masse connue observée à des instants connus, alors les observations seront 
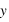".Une première approche est présentée dans la section 1 de la partie "comprendre" - Le problème inverse: étant donné des observations
aux instants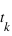 
, 
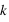=1..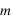
et un modèle 
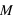(éventuellement un bruit ε), quels sont les paramètres 
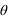? C'est le problème de la réduction des données expérimentales, qui est l'objet de la section 3 de la partie "comprendre". - L'instrumentation: Comment construire des instruments performants et modéliser leurs mesures ? La prise en compte des bruits instrumentaux fait partie du modèle.
- L'interprétation des résultats: Une fois que les paramètres orbitaux pour plusieurs systèmes planétaires ont été estimés (ainsi que l'incertitude associée), on peut se demander ce que ces résultats signifient Il existe dans le cas des exoplanètes une littérature abondante donnant des scénarios de formation planétaire expliquant les valeurs prises par un système donnée, ou la distribution des éléments orbitaux observés.
Ce cours se focalisera sur les trois premières problématiques, car la quatrième est transverse à toutes les techniques d'observation et fait l'objet d'un cours à part entière.
