Décrire
Auteur: Nathan Hara & Jacques Laskar
- Vitesses radiales
- Astrométrie
- Exercices
- Que mesure-t-on ?
- Signal et bruit
- Un problème d'estimation
- Exercices
- Effets à prendre en compte
- Effets à prendre en compte (2)
- Quantifier l'incertitude
- Exercices
Vitesses radiales
Lorsque la distance entre une source d'onde et un observateur varie dans le temps, la longueur d'onde vue par l'observateur varie aussi. Ce phénomène, appelé effet doppler, est ce qui permet la détection du mouvement radial de l'étoile. Cet effet est géométrique, et présent pour tous les types d'ondes. Un exemple bien connu est celui de la sirène d'ambulance: le son qu'elle émet a l'air plus grave une fois qu'elle est passée devant nous. Pour le comprendre, considérons une personne qui se baigne sur une plage (suffisament loin pour que les vagues se brisent derrière elle). Si elle reste statique les vagues vont l'atteindre avec une certaine période. Selon qu'elle s'avance vers le large ou revient vers la plage elle rencontrera les vagues plus fréquemment ou moins fréquemment. De la même manière, plus vite l'étoile s'avance vers la Terre, plus la lumière reçue est décalée vers les hautes fréquences.
L'énergie par longueur d'onde d'une source lumineuse, ou de manière équivalente, le nombre de photons reçus par longueur d'onde, est appelé le spectre de cette source. Cette définition fait intervenir une mesure, le spectre dépend donc de l'observateur. La lumière provenant d'une étoile est composée à priori d'une infinité de longueurs d'ondes. Certaines d'entre elles sont absorbées par l'atmosphère de l'étoile, de sorte qu'elles sont absentes du spectre mesuré. On parle de raies d'absorption. Le spectre d'une étoile a un aspect proche de la figure 1. Si la source lumineuse et l'observateur sont immobiles l'un par rapport à l'autre, l'observateur verra un certain profil spectral 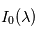 (intensité par longueur d'onde
(intensité par longueur d'onde 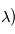 . Si maintenant la source et l'observateur ont une vitesse relative
. Si maintenant la source et l'observateur ont une vitesse relative 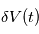 au temps
au temps 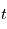 , l'observateur verra un spectre décalé
, l'observateur verra un spectre décalé 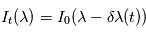 avec
avec 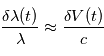 où
où 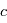 est la vitesse de la lumière, dans l'hypothèse où
est la vitesse de la lumière, dans l'hypothèse où 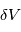 est très petit par rapport à
est très petit par rapport à 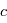 . En mesurant
. En mesurant 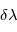 on peut remonter à
on peut remonter à 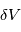 . La présence d'une planète autour d'une étoile engendre un mouvement périodique de celle-ci, donc un décalage périodique du spectre (voir figure 2).
. La présence d'une planète autour d'une étoile engendre un mouvement périodique de celle-ci, donc un décalage périodique du spectre (voir figure 2).
La mesure du décalage du spectre est utilisée depuis la fin du XIXe siècle pour détecter des étoiles binaires. La vitesse de l'étoile dont on observe le spectre (étoile cible) diminue avec le rapport de masse du compagnon et de l'étoile cible. Plus faible est la masse du compagnon plus il est difficile de le détecter. Les techniques ont été perfectionnées pour détecter des compagnons de masses de plus en plus faible.
Remarque: Une des limitations des mesures de vitesse radiale est qu'on ne mesure qu'une masse minimale car on mesure la projection du mouvement selon une direction. En notant 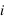 l'angle entre la ligne de visée et le plan orbital d'un objet de masse
l'angle entre la ligne de visée et le plan orbital d'un objet de masse 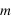 , on mesure
, on mesure 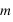
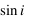 .
.
En 1989, Latham trouve un objet d'une masse minimale de 11 masses de Jupiter (notée 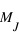 ) en orbite autour d'une étoile de type solaire. Etant
donné que la limite admise à la masse d'une planète (au delà de laquelle le deutérium entre en fusion) est de 13
) en orbite autour d'une étoile de type solaire. Etant
donné que la limite admise à la masse d'une planète (au delà de laquelle le deutérium entre en fusion) est de 13 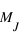 , la conclusion de l'article est encore valide: il est possible que ce compagnon soit une Naine brune ou une super Jupiter, selon la valeur de
, la conclusion de l'article est encore valide: il est possible que ce compagnon soit une Naine brune ou une super Jupiter, selon la valeur de 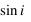 . La première planète confirmée comme telle est découverte en 1995 par Michel Mayor et Didier Queloz à l'observatoire de Haute Provence.
. La première planète confirmée comme telle est découverte en 1995 par Michel Mayor et Didier Queloz à l'observatoire de Haute Provence.
Pour donner une idée des ordres de grandeur considérées, la Terre engendre un déplacement du Soleil d'environ 9 cm/s, Jupiter de 12.5 m/s. Un déplacement d'1 m par seconde correspond à un décalage relatif de longueurs d'onde 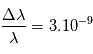 . La précision attendue doit être maintenue sur plusieurs mois, voire plusieurs années.
. La précision attendue doit être maintenue sur plusieurs mois, voire plusieurs années.
Spectre du Soleil dans le visible

Représentation de la lumière du Soleil diffractée dans le visible. Pour une exploration plus précise du spectre du Soleil, voir
cette page.
Crédit :
Observatoire de Paris
Décalage du spectre
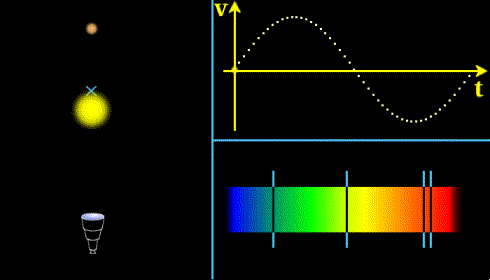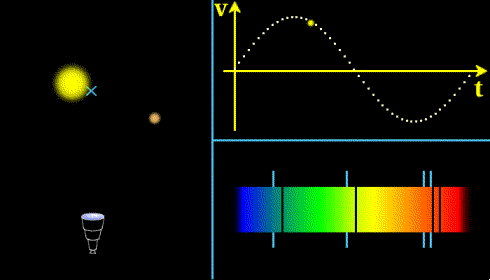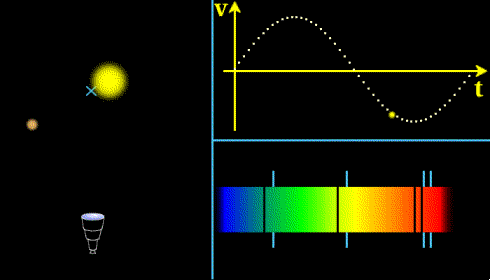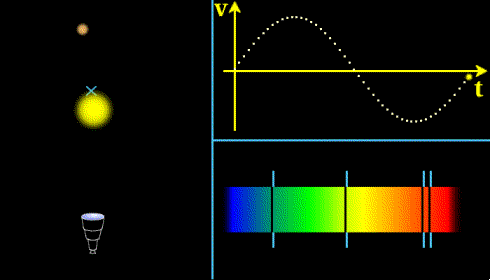
L'étoile et la planète orbitent autour de leur centre de gravité. L'observateur (représenté par une lunette) voit le spectre reçu se décaler et en infère la vitesse V de l'étoile au cours du temps.
Crédit :
Observatoire de Paris, ASM, E. Pécontal
Astrométrie
L'astrométrie désigne la mesure de la position des astres. Chronologiquement, l'astrométrie peut être considérée comme la première discipline de l'astronomie. Les anciens s'étaient déjà aperçus que certains astres semblent mobiles: les planètes, mais l'observation à l'oeil nu et avec les premiers instruments astronomiques sont trop imprécises pour détecter le mouvement des étoiles. Ils pensaient donc qu'elles sont fixes, mais ce n'est pas du tout le cas.
Plus précisément, on mesure la position des astres sur la Sphère céleste: Il s'agit d'une manière d'appeler l'ensemble des coordonnées angulaires d'un système de coordonnées sphériques. Selon le contexte, le centre de centre de ce repère est le barycentre du système solaire ou celui de la Terre, l'observateur, ou un autre point. Les directions du repère fixe peuvent être définies par rapport à des étoiles très lointaines (quasars), ou l'intersection du plan de l'orbite de la Terre (l'ecliptique) et de l'équateur.
Les observations doivent être exprimées dans un même système de référence. En l'occurrence, le repère fixe choisi est le référentiel barycentrique du système solaire qui est un référentiel galiléen. De ce fait, on peut modéliser simplement la trajectoire de l'étoile dans ce référentiel. Si l'étoile a des compagnons planétaires, le mouvement dû aux planètes projeté aura l'aspect d'ellipses imbriquées les unes dans les autres (voire figure). Le mouvement rectiligne uniforme a une amplitude bien supérieure au mouvement dû aux planètes, il n'est pas représenté sur la figure pour cette raison.
Une mesure astrométrique comporte toujours plusieurs étoiles dans le champ, de sorte que l'on peut mesurer le déplacement de l'étoile cible par rapport aux étoiles du champ. Ce qui nous intéresse est en effet un mouvement différentiel (on compare les mesures les unes aux autres, on ne cherche pas une position absolue). Un mouvement global des étoiles du champ provient des turbulences atmosphériques ou de bruits instrumentaux, qui peuvent être corrigés.
En mars 2015, deux planètes on été découvertes par astrométrie (DE0823-49 b et HD 176051 b). La résolution nécessaire à la détection de planètes est difficilement atteignable à cause des perturbations atmosphériques. Pour les corriger, il est possible d'utiliser une technique appelée astrométrie différentielle. Sa présentation sort du cadre de ce cours. Il est probable que la mission astrométrique spatiale GAIA, dont la précision est de l'ordre de 20 μas permettra de faire de nombreuses découvertes.
Les mouvements de l'étoile autour du centre de gravité du système planétaire sont de l'ordre du rayon de l'étoile en général. Par exemple, le mouvement de Jupiter entraine un mouvement quasi circulaire du Soleil dont le rayon est environ 1.06 rayon solaire.
L'ordre de grandeur du déplacement observé dépend de la distance de l'étoile, des masses de l'étoile et de la planète et du demi-grand axe de l'orbite.
ordres de grandeur
| Type de planète | Distance à l'étoile | Amplitude du mouvement |
| Jupiter | 10 parsec | 500 µas |
| 100 parsec | 50 µas |
| Terre | 10 parsec | 0.3 µas |
| 100 parsec | 0.03 µas |
Projection du mouvement de deux planètes sur la sphère céleste
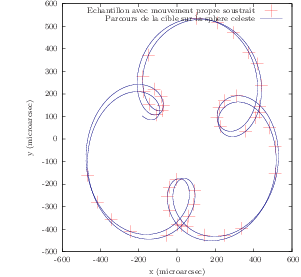
Observations idéales (sans bruit, mouvement de l'étoile uniquement dû aux planètes) d'un système à deux planètes sur cinq ans. En bleu on représente tout le parcours de la planète et en rouge les quarante-cinq mesures de position.
Exercices
Auteur: Nathan Hara
 Questions générales
Questions générales
Difficulté : ☆
Auteur: Nathan Hara
 Vitesses radiales
Vitesses radiales
Difficulté : ☆
Question 1)
- L'effet Doppler existe-t-il seulement pour la lumière ou pour tous les types d'ondes ?
- Est-il dû au déplacement de la source, du receveur, ou à leur vitesse relative ?
Auteur: Nathan Hara
 Astrométrie
Astrométrie
Difficulté : ☆
Notez que si on observait uniquement l'effet de la planète si petit soit-il, on aurait toujours accès à toute l'information. Malheureusement, de nombreuses autre sources perturbent le signal, comme on va le voir dans les pages suivantes.
Que mesure-t-on ?
Le principe de ces techniques de détection est simple, mais pour obtenir la précision désirée il faut prendre en compte une grande quantité d'effets affectant les observations. Les mesures sont issues in fine de capteurs CCD, situés au plan focal d'un télescope ou en sortie d'un spectrographe, respectivement dans les cas de l'astrométrie et de la mesure de vitesses radiales. Ces capteurs fonctionnent par effet photoélectrique: lorsqu'un photon les percute, un électron est émis (si le photon a une énergie supérieure à une certaine limite). Ils sont exposés à la lumière pendant un certain temps appelé temps d'intégration. Le nombre d'électrons reçus pendant ce temps est ensuite compté pixel par pixel. Finalement, on obtient un tableau de nombre: le nombre de photons reçus par pixel de la caméra CCD. A chaque mesure est attachée une erreur, calculée selon une méthode explicitée par l'observateur. On effectue ensuite une série d'opérations mathématiques sur les mesures obtenues pour en extraire l'information souhaitée.
Avant d'arriver sur ces capteurs, les photons passent par les instruments, par l'atmosphère, par le milieu interstellaire. De plus, le mécanisme d'émission des photons par les étoiles est complexe: même si l'étoile était fixe par rapport à l'observateur, son spectre et sa position sembleraient variables. Comme les instruments ne permettent pas de résoudre angulairement l'étoile (elle n'apparait que sur un pixel), on mesure la lumière moyenne de sa photosphère, c'est à dire la fine partie de son enveloppe dont la lumière nous parvient. L'astrométrie est sensible à son photocentre. Enfin, il est possible que la lumière reçue provienne partiellement d'une autre source céleste située à proximité de l'étoile, ou du Soleil.
Chacune de ces étapes affecte le signal reçu, de sorte que l'information recherchée n'en représente qu'une petite partie. Par exemple, la vitese radiale apparente d'une étoile est de l'ordre de quelques dizaines de km/s, les techniques actuelles permettent de réduire le bruit instrumental à un peu moins de 0.3-0.5 m/s, qui est aussi l'ordre de grandeur de l'erreur due à une étoile de type solaire. Le signal d'une planète tellurique est de l'ordre de 0.5 m/s, c'est à dire moins que l'ordre de grandeur du bruit.
Pour chercher des signaux de plus en plus faibles, il faut améliorer à la fois la modélisation du signal, des instruments, et des méthodes de traitement de données.
Représentation du trajet de la lumière
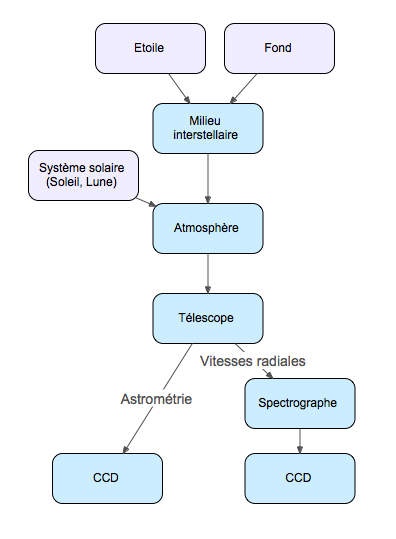
En mauve, les sources de lumière et en bleu les milieux traversés.
Signal et bruit
Idéalement, on voudrait directement avoir accès aux orbites et aux masses exactes des planètes autour d'une étoile donnée. C'est jusqu'à présent impossible, et probablement pour longtemps ! Les techniques dont il est question ici visent à mesurer la position ou la vitesse de l'étoile, ce sont lessignaux recherchés. Cependant, comme on l'a vu page précédente, la quantité effectivement mesurée contient non seulement le signal mais aussi de nombreux processus aléatoires qu'on appelle bruits. Notre problématique est d'extraire les paramètres du signal (les paramètres des orbites) dans des mesures entachées de bruits.
Pour savoir si un signal sera détectable à priori, on calcule le rapport signal sur bruit qui est le rapport de "la puissance du signal" sur "la puissance du bruit". Ce rapport est fondamental. Le sens précis de cette expression varie selon le contexte mais typiquement, si un signal 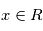 et un bruit
et un bruit 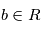 forment une mesure
forment une mesure 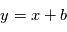 , le rapport signal sur bruit est
, le rapport signal sur bruit est 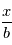 . Plus ce rapport est grand, plus la mesure est précise.
. Plus ce rapport est grand, plus la mesure est précise.
Supposons que l'on veuille estimer une variation de position angulaire ou de vitesse (resp. 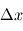 et
et 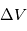 ) d'une étoile de type solaire à 10 parsec autour de laquelle une planète de type jupiter orbite. On a
) d'une étoile de type solaire à 10 parsec autour de laquelle une planète de type jupiter orbite. On a 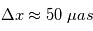 et
et 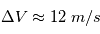 Les mesures sont contaminées par des variations aléatoires d'amplitudes
Les mesures sont contaminées par des variations aléatoires d'amplitudes 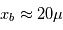 as (précision de la mission Gaia, mission astrométrique la plus précise) et
as (précision de la mission Gaia, mission astrométrique la plus précise) et 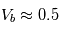 m/s (ordre de grandeur pour les meilleurs spectrographes actuels) . Le rapport signal sur bruit est de l'ordre de
m/s (ordre de grandeur pour les meilleurs spectrographes actuels) . Le rapport signal sur bruit est de l'ordre de 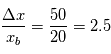 et
et 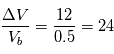 . La technique par vitesse radiale est pour l'instant plus précise.
. La technique par vitesse radiale est pour l'instant plus précise.
Lorsqu'on mesure une quantité modélisée par une variable alétoire (par exemple le nombre de photons reçus pendant une seconde), le rapport signal sur bruit peut être défini comme le rapport de la moyenne et de l'écart-type.
Attention: il ne faut pas confondre l'amplitude d'un effet indésirable et le bruit qui lui est associé. Par exemple, le mouvement de la Terre dans le système solaire induit une vitesse apparente de plusieurs dizaines de km par secondes. Cependant, sa position est connue avec une très bonne précision, de sorte que l'incertitude liée à la soustraction du mouvement de la Terre est de l'ordre d'1 m/s.
Remarque: On distingue en général la précision et l'exactitude. On peut disposer d'un instrument très précis mais comme d'autres effets perturbent la mesure, la mesure donne une valeur inexacte de ce que l'on cherche à mesurer. Dans l'exemple précédent, si on ne soustrait pas la vitesse de la Terre, l'instrument peut être aussi précis qu'on veut on aura un signal parasite entre 1000 et 60000 fois plus gros que celui qu'on cherche à mesurer.
Un problème d'estimation
La problématique de la détection par vitesse radiale et astrométrie est la suivante: quelles sont les orbites et les masses des planètes compagnons de l'étoile cible ? Comme les mesures sont entachées de bruit, on ne peut pas donner des paramètres orbitaux exacts. On estime aussi la "confiance" dans les valeurs des paramètres, souvent donnée sous forme de probabilités. On est aussi amené à se demander si toutes les planètes ont été détectées, et si les détections annoncées sont vraisemblables. En particulier, on étudie la stabilité du système trouvé.
La détection de planètes extrasolaires, comme d'autres problématiques de détection peut être subdivisé comme suit:
- Le problème direct, ou modélisation,Notre problème est bien plus complexe que celui de la page précédente. On ne cherche pas à estimer un paramère
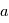 à partir d'une mesure
à partir d'une mesure 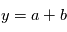 , mais un vecteur de paramètre
, mais un vecteur de paramètre 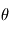 à partir de plusieurs mesures aux instants
à partir de plusieurs mesures aux instants 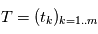 , et les mesures dépendent de ces paramètres et des instants d'observations par une fonction
, et les mesures dépendent de ces paramètres et des instants d'observations par une fonction 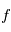 : on a
: on a 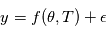 , où
, où 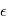 est une variable aléatoire suivant une certaine loi de probabilité qui modélise l'incertitude. Le problème direct est la construction de la fonction
est une variable aléatoire suivant une certaine loi de probabilité qui modélise l'incertitude. Le problème direct est la construction de la fonction 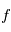 . En l'occurrence, on utilise les équations bien connues de la mécanique céleste. "Si des planètes avec des paramètres orbitaux connus orbitent autour d'une étoile de masse connue observée à des instants connus, alors les observations seront
. En l'occurrence, on utilise les équations bien connues de la mécanique céleste. "Si des planètes avec des paramètres orbitaux connus orbitent autour d'une étoile de masse connue observée à des instants connus, alors les observations seront 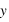 ".Une première approche est présentée dans la section 1 de la partie "comprendre"
".Une première approche est présentée dans la section 1 de la partie "comprendre" - Le problème inverse: étant donné des observations
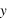 aux instants
aux instants 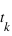 ,
, 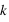 =1..
=1..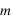 et un modèle
et un modèle 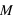 (éventuellement un bruit ε), quels sont les paramètres
(éventuellement un bruit ε), quels sont les paramètres 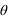 ? C'est le problème de la réduction des données expérimentales, qui est l'objet de la section 3 de la partie "comprendre".
? C'est le problème de la réduction des données expérimentales, qui est l'objet de la section 3 de la partie "comprendre". - L'instrumentation: Comment construire des instruments performants et modéliser leurs mesures ? La prise en compte des bruits instrumentaux fait partie du modèle.
- L'interprétation des résultats: Une fois que les paramètres orbitaux pour plusieurs systèmes planétaires ont été estimés (ainsi que l'incertitude associée), on peut se demander ce que ces résultats signifient Il existe dans le cas des exoplanètes une littérature abondante donnant des scénarios de formation planétaire expliquant les valeurs prises par un système donnée, ou la distribution des éléments orbitaux observés.
Ce cours se focalisera sur les trois premières problématiques, car la quatrième est transverse à toutes les techniques d'observation et fait l'objet d'un cours à part entière.
Exercices
 Modélisation
Modélisation
Difficulté : ☆
Question 1)
- Quelles sont les précisions annoncées des spectrographes européens ELODIE, HARPS et de celui à venir ESPRESSO ?
- Les observateurs attendent que le Soleil soit couché depuis plusieurs dizaines de minutes avant de commencer leurs observations, pourquoi ?
- Quel désavantages a-t-on à observer une étoile proche de la Lune ?
- Pourquoi observer en altitude ?
Effets à prendre en compte
Les observations traitées sont des mesures de position sur le plan focal d'un télescope et des mesures de spectres lumineux; respectivement pour l'astrométrie et les vitesses radiales. Faire l'hypothèse que les mesures ne sont que le résultat du mouvement d'une étoile parfaitement homogène donnerait des résultats invraisemblables. La fonction 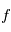 de la page précédente prend en général en compte plusieurs effets présentés ici. Compte tenu du format du cours, seuls certains d'entre eux seront développés dans la suite.
de la page précédente prend en général en compte plusieurs effets présentés ici. Compte tenu du format du cours, seuls certains d'entre eux seront développés dans la suite.
- Bruit de photon: il s'agit d'un bruit dû à la quantification de la lumière. Les photons sont émis aléatoirement selon ce qu'on appelle un "flux poissonien". Si un détecteur observe une source émettant en moyenne
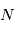 photons sur un certain intervalle de temps
photons sur un certain intervalle de temps 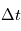 , le nombre de détections pendant
, le nombre de détections pendant 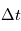 sera une variable aléatoire de moyenne
sera une variable aléatoire de moyenne 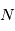 et de variance
et de variance 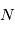 . Cette notion est expliquée plus en détail page bruit de photon
. Cette notion est expliquée plus en détail page bruit de photon - Bruit instrumental: les instruments se comportent en pratique différemment de leurs idéalisation de manière imprévisible. Le miroir du télescope est sensible aux variations de température, l'utilisation d'équipement électronique induit du bruit grenaille (similaire au bruit de photon) et du bruit thermique. Il s'agit de toutes les erreurs dues au trajet de la lumière depuis l'entrée du télescope jusqu'à la lecture du détecteur CCD. Ce bruit peut être déterminé par étalonnage.
- Les bruits stellaires: A chaque longueur d'onde
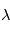 , on observe le flux lumineux
, on observe le flux lumineux 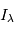 provenant de toute la partie visible de l'étoile. D'un point de vue mathématique,
provenant de toute la partie visible de l'étoile. D'un point de vue mathématique, 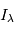 est intégré sur toute le disque visible de la photosphère de l'étoile:
est intégré sur toute le disque visible de la photosphère de l'étoile: 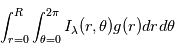 . Au rayon
. Au rayon  et à l'angle
et à l'angle 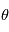 ,
, 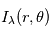 dépend de la température, de la composition et de la vitesse de la matière par rapport à l'observateur en
dépend de la température, de la composition et de la vitesse de la matière par rapport à l'observateur en 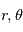 .
. 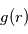 est un facteur variant selon les modèles dits de "limb darkening". On peut modéliser des propriétés des variations du flux à une longueur d'onde donnée avec un modèle physique de l'étoile.
En pratique, on prend en compte trois types d'effets en compte:
est un facteur variant selon les modèles dits de "limb darkening". On peut modéliser des propriétés des variations du flux à une longueur d'onde donnée avec un modèle physique de l'étoile.
En pratique, on prend en compte trois types d'effets en compte: - les oscillations acoustiques (p-modes): la propagation d'ondes mécaniques dans la couche extérieure de l'étoile provoque une contraction/dilatation radiale, qui a une signature de quelques centimètres par seconde dans les données de vitesses radiales (cette vidéo montre une simulation des ondes mécaniques au sein d'une étoile).
- les tâches dues à l'activité magnétique: Le champ magnétique à la surface de l'étoile peut "piéger" localement du plasma, qui se refroidit et devient donc moins lumineux. Ce phénomène a des effets à court terme: une tache présente sur un des côtés de l'étoile brise la symétrie entre la partie "rouge" et la partie "bleue" (voir figure). D'autre part, sur une période d'observation le nombre de taches peut varier de zéro à plusieurs centaines. Lorsque la convection est inhibée par le champ magnétique l'étoile apparaît plus froide, globalement décalée vers le rouge.
- La granulation: la surface de l'étoile étant plus froide que son centre, du gaz chaud remonte à la surface, se refroidit en émettant de la lumière puis redescend. Ce phénomène de convection crée des inhomogénéités de luminosité sur la suface de l'étoile dont la somme donne une vitesse radiale apparente, ou un déplacement du photocentre.
Selon le type d'étoile, ces bruits sont d'importances variables. Certaines étoiles sont trop actives pour avoir une chance de détecter une planète de masse tellurique.
Intensité globale
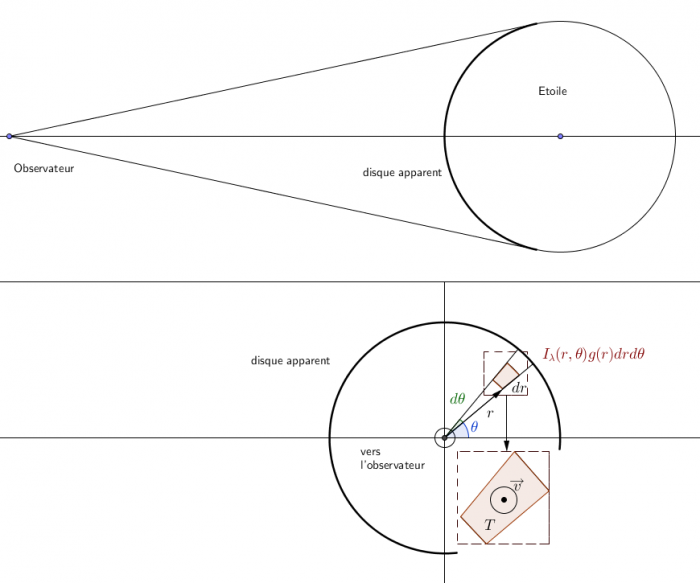
L'intensité dépend de la composition, de la température
et de la vitesse
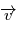
en chaque point du disque apparent de l'étoile
Effet de la rotation de l'étoile sur le spectre
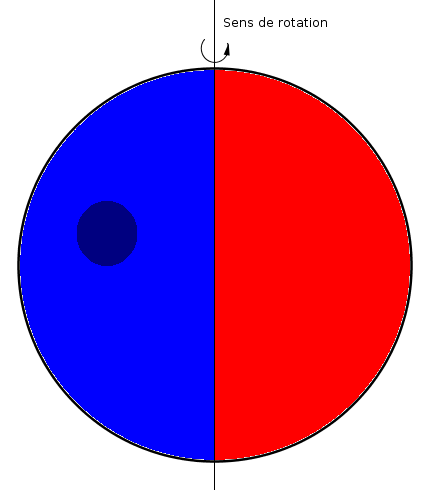
La lumière provenant de la moitié de l'étoile ayant un mouvement vers l'observateur est décalé vers les hautes fréquences (vers le bleu). L'autre moitié est décalée vers les basses fréquences (vers le rouge). Dans l'hypothèse où l'étoile est sphérique, et a une luminosité identique partout sur sa surface, le décalage vers le rouge et celui vers le bleu ne fait qu'élargir les raies spectrales. Si une tache est présente, ici sur la partie bleue, la symétrie est brisée et le déficit de lumière entraine un décalage du spectre vers le rouge.
Effets à prendre en compte (2)
- Contamination du fond: à cause de la diffraction, il est impossible d'observer un point du ciel, observe toujours le flux moyen d'une certaine région du ciel. Ce flux ne provient pas nécessairement uniquement de l'objet observé. Cette prise en compte est particulièrement importante lorsque l'étoile est dans un système binaire. En effet, Comme un compagnon planétaire, l'autre étoile engendre un mouvement elliptique de l'étoile cible de plus grande amplitude que celui provoqué par une planète. De plus, si la séparation angulaire entre les deux étoiles est plus petite que le champs de vue, la lumière provenant de la seconde étoile contamine les observations.
- Système multiple: l'étoile cible peut avoir un mouvement dû à la présence d'autres étoiles proches.
- Les perturbations atmosphériques: les turbulences de l'atmosphère aux hautes altitudes font que le signal est diffracté aléatoirement.
- La parallaxe: Le mouvement de l'étoile est modélisé dans un référentiel galiléen dont le référentiel barycentrique du système solaire est une approximation. Cependant, les observations ne sont évidemment pas disponibles depuis le centre du système solaire. Il faut prendre en compte le mouvement de l'observateur, qui se manifeste par un mouvement apparent de l'astre.
Quantifier l'incertitude
Pour pouvoir annoncer qu'une planète a été découverte, il faut avoir une certaine confiance dans le résultat. Cependant, comme on vient de le voir, les mesures sont contaminées par de nombreuses sources qui peuvent être aléatoires. La détection d'exoplanète, comme toutes les problématiques de détection en astronomie, donne l'occasion de présenter des modélisations de phénomènes aléatoires. Introduire ces outils permettra en particulier de définir proprement ce que sont les barres d'erreurs. On donnera un sens à une phrase comme: la période d'une orbite estimée est 100 jours, plus ou moins 10 jours à trois sigmas.
Le cadre mathématique utilisé pour les prendre en compte est la théorie des statistiques. Les quantités physiques dont le comportement est imprévisible sont modélisées par des variables aléatoires qui prennent une certaine valeur à chaque mesure. Etant donné que cette notion intervient dans:
- La modélisation des variations de luminosité de l'étoile
- La modélisation des perturbations atmosphériques
- Le calcul de la précision de l'instrument
- Le calcul des incertitudes sur les paramètres des orbites estimées
On donnera une description fonctionnelle, permettant de comprendre le cours sans avoir besoin de rentrer dans les détails des statistiques. Le lecteur intéressé pourra se référer à un ouvrage spécialisé, par exemple le cours de Didier Pelat (en libre accès), cité dans la bibliographie.
Une variable alétoire 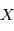 peut être vue comme un programme informatique donnant une valeur réelle à chaque fois qu'on lui demande. La valeur retournée dépendra de la distribution de probabilité de cette variable aléatoire, notée
peut être vue comme un programme informatique donnant une valeur réelle à chaque fois qu'on lui demande. La valeur retournée dépendra de la distribution de probabilité de cette variable aléatoire, notée 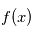 . Par exemple, si on veut modéliser le lancer d'une pièce de monnaie, chaque lancé correspond à une requête au programme qui retournera "face" ou "pile" avec une probabilité 1/2. Dans le cas de distributions continues,
. Par exemple, si on veut modéliser le lancer d'une pièce de monnaie, chaque lancé correspond à une requête au programme qui retournera "face" ou "pile" avec une probabilité 1/2. Dans le cas de distributions continues, 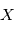 prendra une valeur entre
prendra une valeur entre 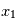 et
et 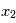 avec une probabilité
avec une probabilité 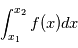 . La distribution la plus utilisée est la gaussienne (parfois appelée courbe en cloche), elle vérifie
. La distribution la plus utilisée est la gaussienne (parfois appelée courbe en cloche), elle vérifie 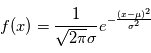 où
où 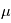 est sa moyenne et
est sa moyenne et 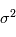 est sa variance. L'analyse des données repose sur l'hypothèse que nous observations des réalisations d'une variable aléatoire. Comme si réaliser une expérience consistait à demander à un ordinateur de sortir une valeur (la mesure) avec une certaine loi de probabilité.
est sa variance. L'analyse des données repose sur l'hypothèse que nous observations des réalisations d'une variable aléatoire. Comme si réaliser une expérience consistait à demander à un ordinateur de sortir une valeur (la mesure) avec une certaine loi de probabilité.
Les variables aléatoires ont deux caractéristiques particulièrement importantes: leur moyenne et leur variance, définie respectivement comme 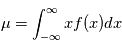 et
et 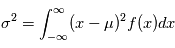 . La racine carére de la variance est appelée l'écart-type. Cette quantité donne "l'écart-typique" à la moyenne des réalisations. Dans la plupart des cas et en particulier dans le cas gaussien, l'écart-type a une interprétation univoque: il quantifie les déviations à la moyenne. Plus il est petit, plus les valeurs éloignées de la moyenne seront improbables. Dans la limite ou l'écart-type tend vers 0, on aura une variable aléatoire certaine, qui prend la valeur
. La racine carére de la variance est appelée l'écart-type. Cette quantité donne "l'écart-typique" à la moyenne des réalisations. Dans la plupart des cas et en particulier dans le cas gaussien, l'écart-type a une interprétation univoque: il quantifie les déviations à la moyenne. Plus il est petit, plus les valeurs éloignées de la moyenne seront improbables. Dans la limite ou l'écart-type tend vers 0, on aura une variable aléatoire certaine, qui prend la valeur 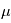 avec une probabilité 1. En physique, on manipule souvent des incertitudes, qui sont implicitement modélisées comme des écart-types de variables aléatoires. Si un observateur dit "j'ai mesuré une vitesse radiale de
avec une probabilité 1. En physique, on manipule souvent des incertitudes, qui sont implicitement modélisées comme des écart-types de variables aléatoires. Si un observateur dit "j'ai mesuré une vitesse radiale de 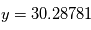 km/s avec une incertitude de
km/s avec une incertitude de 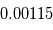 km/s", implicitement on suppose qu'il existe une variable aléatoire dont la moyenne correspond à la "vraie" valeur de la vitesse radiale et dont l'écart-type vaut
km/s", implicitement on suppose qu'il existe une variable aléatoire dont la moyenne correspond à la "vraie" valeur de la vitesse radiale et dont l'écart-type vaut 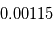 km/s.
km/s.
Remarque: nous utilisons une terminologie vague, pour des définitions précises voir les références.
Exercices
Auteur: Nathan Hara
 Modélisation des vitesses radiales
Modélisation des vitesses radiales
Difficulté : ☆
Question 1)
Citer des éléments à prendre en compte dans la modélisation des mesures de vitesses radiales ou astrométriques (on ne demande pas une liste très précise, encore moins exhaustive).
 Modélisations
Modélisations
Difficulté : ☆☆
Réponses aux exercices
pages_ind-vr/exercice1.html
Exercice
'Astrométrie'
- Question 1
Aide :
- 1 µas =
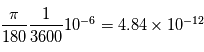
- Si
 est en radian
est en radian  , le jongleur doit se trouver à
, le jongleur doit se trouver à 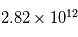 m = 19 UA, soit environ la distance Terre-Uranus.
m = 19 UA, soit environ la distance Terre-Uranus.
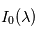 (intensité par longueur d'onde
(intensité par longueur d'onde 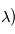 . Si maintenant la source et l'observateur ont une vitesse relative
. Si maintenant la source et l'observateur ont une vitesse relative 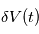 au temps
au temps 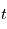 , l'observateur verra un spectre décalé
, l'observateur verra un spectre décalé 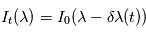 avec
avec 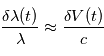 où
où  est la vitesse de la lumière, dans l'hypothèse où
est la vitesse de la lumière, dans l'hypothèse où 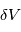 est très petit par rapport à
est très petit par rapport à 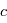 . En mesurant
. En mesurant 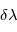 on peut remonter à
on peut remonter à 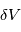 . La présence d'une planète autour d'une étoile engendre un mouvement périodique de celle-ci, donc un décalage périodique du spectre (voir figure 2).
. La présence d'une planète autour d'une étoile engendre un mouvement périodique de celle-ci, donc un décalage périodique du spectre (voir figure 2).
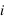 l'angle entre la ligne de visée et le plan orbital d'un objet de masse
l'angle entre la ligne de visée et le plan orbital d'un objet de masse 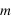 , on mesure
, on mesure 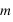
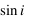 .
.
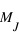 ) en orbite autour d'une étoile de type solaire. Etant
donné que la limite admise à la masse d'une planète (au delà de laquelle le deutérium entre en fusion) est de 13
) en orbite autour d'une étoile de type solaire. Etant
donné que la limite admise à la masse d'une planète (au delà de laquelle le deutérium entre en fusion) est de 13 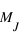 , la conclusion de l'article est encore valide: il est possible que ce compagnon soit une Naine brune ou une super Jupiter, selon la valeur de
, la conclusion de l'article est encore valide: il est possible que ce compagnon soit une Naine brune ou une super Jupiter, selon la valeur de 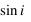 . La première planète confirmée comme telle est découverte en 1995 par Michel Mayor et Didier Queloz à l'observatoire de Haute Provence.
. La première planète confirmée comme telle est découverte en 1995 par Michel Mayor et Didier Queloz à l'observatoire de Haute Provence.
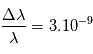 . La précision attendue doit être maintenue sur plusieurs mois, voire plusieurs années.
. La précision attendue doit être maintenue sur plusieurs mois, voire plusieurs années.



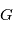 (ou centre de gravité). Si une seule planète de masse
(ou centre de gravité). Si une seule planète de masse 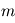 orbite autour d'une étoile de masse
orbite autour d'une étoile de masse 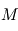 à une distance
à une distance 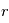 de
de 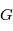 que vaut la distance de l'étoile à
que vaut la distance de l'étoile à 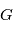 , notée
, notée 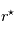 ? Que pensez vous de l'affirmation: "à orbite fixée, plus une planète est massive plus elle est facile à détecter" ?
? Que pensez vous de l'affirmation: "à orbite fixée, plus une planète est massive plus elle est facile à détecter" ?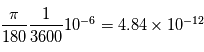
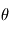 est en radian
est en radian 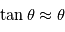 , le jongleur doit se trouver à
, le jongleur doit se trouver à 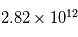 m = 19 UA, soit environ la distance Terre-Uranus.
m = 19 UA, soit environ la distance Terre-Uranus. 
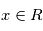 et un bruit
et un bruit 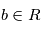 forment une mesure
forment une mesure 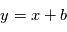 , le rapport signal sur bruit est
, le rapport signal sur bruit est 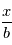 . Plus ce rapport est grand, plus la mesure est précise.
. Plus ce rapport est grand, plus la mesure est précise.
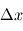 et
et 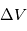 ) d'une étoile de type solaire à 10 parsec autour de laquelle une planète de type jupiter orbite. On a
) d'une étoile de type solaire à 10 parsec autour de laquelle une planète de type jupiter orbite. On a 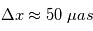 et
et 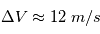 Les mesures sont contaminées par des variations aléatoires d'amplitudes
Les mesures sont contaminées par des variations aléatoires d'amplitudes 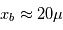 as (précision de la mission Gaia, mission astrométrique la plus précise) et
as (précision de la mission Gaia, mission astrométrique la plus précise) et 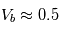 m/s (ordre de grandeur pour les meilleurs spectrographes actuels) . Le rapport signal sur bruit est de l'ordre de
m/s (ordre de grandeur pour les meilleurs spectrographes actuels) . Le rapport signal sur bruit est de l'ordre de 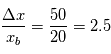 et
et 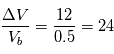 . La technique par vitesse radiale est pour l'instant plus précise.
. La technique par vitesse radiale est pour l'instant plus précise.
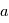 à partir d'une mesure
à partir d'une mesure 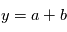 , mais un vecteur de paramètre
, mais un vecteur de paramètre 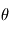 à partir de plusieurs mesures aux instants
à partir de plusieurs mesures aux instants 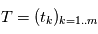 , et les mesures dépendent de ces paramètres et des instants d'observations par une fonction
, et les mesures dépendent de ces paramètres et des instants d'observations par une fonction 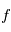 : on a
: on a 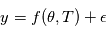 , où
, où 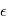 est une variable aléatoire suivant une certaine loi de probabilité qui modélise l'incertitude. Le problème direct est la construction de la fonction
est une variable aléatoire suivant une certaine loi de probabilité qui modélise l'incertitude. Le problème direct est la construction de la fonction 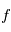 . En l'occurrence, on utilise les équations bien connues de la mécanique céleste. "Si des planètes avec des paramètres orbitaux connus orbitent autour d'une étoile de masse connue observée à des instants connus, alors les observations seront
. En l'occurrence, on utilise les équations bien connues de la mécanique céleste. "Si des planètes avec des paramètres orbitaux connus orbitent autour d'une étoile de masse connue observée à des instants connus, alors les observations seront 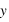 ".Une première approche est présentée dans la section 1 de la partie "comprendre"
".Une première approche est présentée dans la section 1 de la partie "comprendre"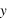 aux instants
aux instants 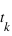 ,
, 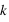 =1..
=1..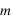 et un modèle
et un modèle 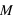 (éventuellement un bruit
(éventuellement un bruit 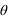 ? C'est le problème de la réduction des données expérimentales, qui est l'objet de la section 3 de la partie "comprendre".
? C'est le problème de la réduction des données expérimentales, qui est l'objet de la section 3 de la partie "comprendre".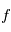 de la page précédente prend en général en compte plusieurs effets présentés ici. Compte tenu du format du cours, seuls certains d'entre eux seront développés dans la suite.
de la page précédente prend en général en compte plusieurs effets présentés ici. Compte tenu du format du cours, seuls certains d'entre eux seront développés dans la suite.
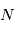 photons sur un certain intervalle de temps
photons sur un certain intervalle de temps 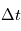 , le nombre de détections pendant
, le nombre de détections pendant 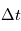 sera une variable aléatoire de moyenne
sera une variable aléatoire de moyenne 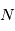 et de variance
et de variance 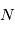 . Cette notion est expliquée plus en détail page
. Cette notion est expliquée plus en détail page 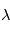 , on observe le flux lumineux
, on observe le flux lumineux 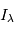 provenant de toute la partie visible de l'étoile. D'un point de vue mathématique,
provenant de toute la partie visible de l'étoile. D'un point de vue mathématique, 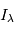 est intégré sur toute le disque visible de la photosphère de l'étoile:
est intégré sur toute le disque visible de la photosphère de l'étoile: 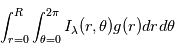 . Au rayon
. Au rayon  et à l'angle
et à l'angle 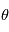 ,
, 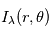 dépend de la température, de la composition et de la vitesse de la matière par rapport à l'observateur en
dépend de la température, de la composition et de la vitesse de la matière par rapport à l'observateur en 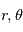 .
. 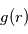 est un facteur variant selon les modèles dits de "limb darkening". On peut modéliser des propriétés des variations du flux à une longueur d'onde donnée avec un modèle physique de l'étoile.
En pratique, on prend en compte trois types d'effets en compte:
est un facteur variant selon les modèles dits de "limb darkening". On peut modéliser des propriétés des variations du flux à une longueur d'onde donnée avec un modèle physique de l'étoile.
En pratique, on prend en compte trois types d'effets en compte: 
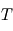 et de la vitesse
et de la vitesse 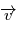 en chaque point du disque apparent de l'étoile
en chaque point du disque apparent de l'étoile

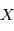 peut être vue comme un programme informatique donnant une valeur réelle à chaque fois qu'on lui demande. La valeur retournée dépendra de la distribution de probabilité de cette variable aléatoire, notée
peut être vue comme un programme informatique donnant une valeur réelle à chaque fois qu'on lui demande. La valeur retournée dépendra de la distribution de probabilité de cette variable aléatoire, notée 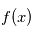 . Par exemple, si on veut modéliser le lancer d'une pièce de monnaie, chaque lancé correspond à une requête au programme qui retournera "face" ou "pile" avec une probabilité 1/2. Dans le cas de distributions continues,
. Par exemple, si on veut modéliser le lancer d'une pièce de monnaie, chaque lancé correspond à une requête au programme qui retournera "face" ou "pile" avec une probabilité 1/2. Dans le cas de distributions continues, 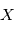 prendra une valeur entre
prendra une valeur entre 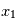 et
et 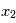 avec une probabilité
avec une probabilité 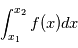 . La distribution la plus utilisée est la gaussienne (parfois appelée courbe en cloche), elle vérifie
. La distribution la plus utilisée est la gaussienne (parfois appelée courbe en cloche), elle vérifie 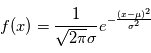 où
où 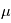 est sa moyenne et
est sa moyenne et 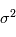 est sa variance. L'analyse des données repose sur l'hypothèse que nous observations des réalisations d'une variable aléatoire. Comme si réaliser une expérience consistait à demander à un ordinateur de sortir une valeur (la mesure) avec une certaine loi de probabilité.
est sa variance. L'analyse des données repose sur l'hypothèse que nous observations des réalisations d'une variable aléatoire. Comme si réaliser une expérience consistait à demander à un ordinateur de sortir une valeur (la mesure) avec une certaine loi de probabilité.
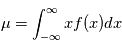 et
et 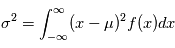 . La racine carére de la variance est appelée l'écart-type. Cette quantité donne "l'écart-typique" à la moyenne des réalisations. Dans la plupart des cas et en particulier dans le cas gaussien, l'écart-type a une interprétation univoque: il quantifie les déviations à la moyenne. Plus il est petit, plus les valeurs éloignées de la moyenne seront improbables. Dans la limite ou l'écart-type tend vers 0, on aura une variable aléatoire certaine, qui prend la valeur
. La racine carére de la variance est appelée l'écart-type. Cette quantité donne "l'écart-typique" à la moyenne des réalisations. Dans la plupart des cas et en particulier dans le cas gaussien, l'écart-type a une interprétation univoque: il quantifie les déviations à la moyenne. Plus il est petit, plus les valeurs éloignées de la moyenne seront improbables. Dans la limite ou l'écart-type tend vers 0, on aura une variable aléatoire certaine, qui prend la valeur 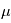 avec une probabilité 1. En physique, on manipule souvent des incertitudes, qui sont implicitement modélisées comme des écart-types de variables aléatoires. Si un observateur dit "j'ai mesuré une vitesse radiale de
avec une probabilité 1. En physique, on manipule souvent des incertitudes, qui sont implicitement modélisées comme des écart-types de variables aléatoires. Si un observateur dit "j'ai mesuré une vitesse radiale de 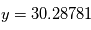 km/s avec une incertitude de
km/s avec une incertitude de 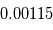 km/s", implicitement on suppose qu'il existe une variable aléatoire dont la moyenne correspond à la "vraie" valeur de la vitesse radiale et dont l'écart-type vaut
km/s", implicitement on suppose qu'il existe une variable aléatoire dont la moyenne correspond à la "vraie" valeur de la vitesse radiale et dont l'écart-type vaut 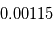 km/s.
km/s.
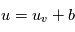 , où
, où 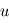 est la tension mesurée,
est la tension mesurée, 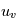 la tension vraie et
la tension vraie et 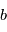 un bruit gaussien dû aux fluctuations intrinsèques de la tension et aux erreurs de mesure. On peut aussi supposer que le voltmètre réalise en réalité une moyenne de tensions sur un certain intervalle de temps.
un bruit gaussien dû aux fluctuations intrinsèques de la tension et aux erreurs de mesure. On peut aussi supposer que le voltmètre réalise en réalité une moyenne de tensions sur un certain intervalle de temps.