Quantifier l'incertitude

Auteur: Nathan Hara & Jacques Laskar

Pour pouvoir annoncer qu'une planète a été découverte, il faut avoir une certaine confiance dans le résultat. Cependant, comme on vient de le voir, les mesures sont contaminées par de nombreuses sources qui peuvent être aléatoires. La détection d'exoplanète, comme toutes les problématiques de détection en astronomie, donne l'occasion de présenter des modélisations de phénomènes aléatoires. Introduire ces outils permettra en particulier de définir proprement ce que sont les barres d'erreurs. On donnera un sens à une phrase comme: la période d'une orbite estimée est 100 jours, plus ou moins 10 jours à trois sigmas.

Le cadre mathématique utilisé pour les prendre en compte est la théorie des statistiques. Les quantités physiques dont le comportement est imprévisible sont modélisées par des variables aléatoires qui prennent une certaine valeur à chaque mesure. Etant donné que cette notion intervient dans:

La modélisation des variations de luminosité de l'étoile
La modélisation des perturbations atmosphériques
Le calcul de la précision de l'instrument
Le calcul des incertitudes sur les paramètres des orbites estimées

On donnera une description fonctionnelle, permettant de comprendre le cours sans avoir besoin de rentrer dans les détails des statistiques. Le lecteur intéressé pourra se référer à un ouvrage spécialisé, par exemple le cours de Didier Pelat (en libre accès), cité dans la bibliographie.

Une variable alétoire 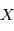peut être vue comme un programme informatique donnant une valeur réelle à chaque fois qu'on lui demande. La valeur retournée dépendra de la distribution de probabilité de cette variable aléatoire, notée 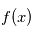f(x) . Par exemple, si on veut modéliser le lancer d'une pièce de monnaie, chaque lancé correspond à une requête au programme qui retournera "face" ou "pile" avec une probabilité 1/2. 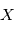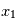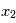Dans le cas de distributions continues, prendra une valeur entre x_1 et x_2 avec une probabilité 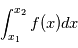$\int_{x_1}^{x_2} f(x) dx$ . 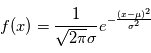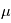La distribution la plus utilisée est la gaussienne (parfois appelée courbe en cloche), elle vérifie $f(x) = \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^2}{\sigma^2}}$ où $\mu$ est sa moyenne et 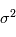$\sigma^2$ est sa variance. L'analyse des données repose sur l'hypothèse que nous observations des réalisations d'une variable aléatoire. Comme si réaliser une expérience consistait à demander à un ordinateur de sortir une valeur (la mesure) avec une certaine loi de probabilité.

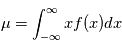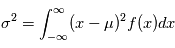Les variables aléatoires ont deux caractéristiques particulièrement importantes: leur moyenne et leur variance, définie respectivement comme $\mu = \int_{-\infty}^\infty xf(x)dx$ et $\sigma^2 = \int_{-\infty}^\infty (x-\mu)^2f(x)dx$ . La racine carére de la variance est appelée l'écart-type. Cette quantité donne "l'écart-typique" à la moyenne des réalisations. Dans la plupart des cas et en particulier dans le cas gaussien, l'écart-type a une interprétation univoque: il quantifie les déviations à la moyenne. Plus il est petit, plus les valeurs éloignées de la moyenne seront improbables. Dans la limite ou l'écart-type tend vers 0, on aura une variable aléatoire certaine, qui prend la valeur 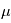$\mu$ avec une probabilité 1. En physique, on manipule souvent des incertitudes, qui sont implicitement modélisées comme des écart-types de variables aléatoires. Si un observateur dit "j'ai mesuré une vitesse radiale de 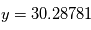y = 30.28781 km/s avec une incertitude de 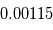0.00115 km/s", implicitement on suppose qu'il existe une variable aléatoire dont la moyenne correspond à la "vraie" valeur de la vitesse radiale et dont l'écart-type vaut 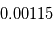0.00115 km/s.

Remarque: nous utilisons une terminologie vague, pour des définitions précises voir les références.