Signal et bruit

Idéalement, on voudrait directement avoir accès aux orbites et aux masses exactes des planètes autour d'une étoile donnée. C'est jusqu'à présent impossible, et probablement pour longtemps ! Les techniques dont il est question ici visent à mesurer la position ou la vitesse de l'étoile, ce sont lessignaux recherchés. Cependant, comme on l'a vu page précédente, la quantité effectivement mesurée contient non seulement le signal mais aussi de nombreux processus aléatoires qu'on appelle bruits. Notre problématique est d'extraire les paramètres du signal (les paramètres des orbites) dans des mesures entachées de bruits.

Pour savoir si un signal sera détectable à priori, on calcule le rapport signal sur bruit qui est le rapport de "la puissance du signal" sur "la puissance du bruit". Ce rapport est fondamental. Le sens précis de cette expression varie selon le contexte mais typiquement, si un signal 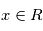et un bruit 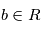forment une mesure 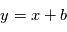, le rapport signal sur bruit est 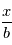. Plus ce rapport est grand, plus la mesure est précise.

Supposons que l'on veuille estimer une variation de position angulaire ou de vitesse (resp. 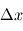et 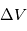) d'une étoile de type solaire à 10 parsec autour de laquelle une planète de type jupiter orbite. On a 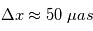et 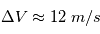Les mesures sont contaminées par des variations aléatoires d'amplitudes 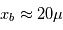as (précision de la mission Gaia, mission astrométrique la plus précise) et 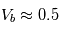m/s (ordre de grandeur pour les meilleurs spectrographes actuels) . Le rapport signal sur bruit est de l'ordre de 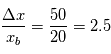et 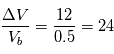. La technique par vitesse radiale est pour l'instant plus précise.

Lorsqu'on mesure une quantité modélisée par une variable alétoire (par exemple le nombre de photons reçus pendant une seconde), le rapport signal sur bruit peut être défini comme le rapport de la moyenne et de l'écart-type.

Attention: il ne faut pas confondre l'amplitude d'un effet indésirable et le bruit qui lui est associé. Par exemple, le mouvement de la Terre dans le système solaire induit une vitesse apparente de plusieurs dizaines de km par secondes. Cependant, sa position est connue avec une très bonne précision, de sorte que l'incertitude liée à la soustraction du mouvement de la Terre est de l'ordre d'1 m/s. Remarque: On distingue en général la précision et l'exactitude. On peut disposer d'un instrument très précis mais comme d'autres effets perturbent la mesure, la mesure donne une valeur inexacte de ce que l'on cherche à mesurer. Dans l'exemple précédent, si on ne soustrait pas la vitesse de la Terre, l'instrument peut être aussi précis qu'on veut on aura un signal parasite entre 1000 et 60000 fois plus gros que celui qu'on cherche à mesurer.