Introduction à la cinématique et la dynamique

Maintenant que nous avons étudié les différentes façons de décrire l'orientation d'un repère à l'instant t, nous pouvons introduire la notion de mouvement. Les équations du mouvement sont un aspect essentiel de la conception et de la réalisation d'un système de contrôle d'attitude car elles régissent la position au cours du temps des objets considérés. Ces équations peuvent être séparées en deux catégories :

• Lorsque nous étudions l'orientation relative de deux référentiels en fonction du temps, nous sommes dans le domaine de la cinématique. Elle recouvre les aspects du mouvement qui peuvent être analysés sans considérer les forces et les couples.
• À l'instant où les forces et les couples sont introduits, on entre dans le domaine de la dynamique.

Afin de clarifier les choses, prenons une particule ponctuelle de la physique newtonienne. Si représente sa position, 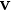sa vitesse et que les dérivées temporelles sont indiquées par un point, alors l'équation cinématique du mouvement s'écrit . L'équation dynamique du mouvement quant à elle s'écrit dans un repère galiléen 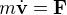ou , avec 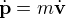la quantité de mouvement, 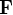la résultante des forces appliquées et 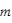la masse de la particule. Comme vous le verrez par la suite, dès lors que l'on s'intéresse aux mouvement d'attitude (autour du centre d'inertie), les vecteur de position et de vitesse sont respectivement remplacés par la matrice d'attitude et le vecteur de vitesse angulaire 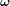. Les forces et quantités de mouvement sont quant à elles remplacées par le couple et le moment angulaire . La cinématique et la dynamique du mouvement rotationnel, ou d'attitude, sont plus compliquées que celles du mouvement de translation. Elles sont détaillées dans la section suivante.