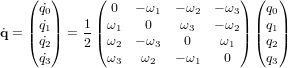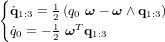Cinématique du satellite : Page pour l'impression

La cinématique est l'étude du mouvement en fonction du temps indépendammant des causes produisant ce mouvement. Elle est utilisée pour décrire la trajectoire du centre de masse d'un satellite dans l'espace.

Bases de la cinématique

Des cours sur ce sujet existent un peu partout, nous rappellerons simplement quelques notions de base ici :

Le vecteur position d'un objet dans un repère est le vecteur $\bold r$ allant de l'origine du repère au centre de l'objet
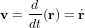
Le vitesse de l'objet dans ce repère s'exprime : $\bold v = {d \over dt}(\bold r) = \dot{\bold r}$
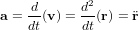
L'accélération de M dans ce même référentiel est : $\bold a = {d \over dt}(\bold v) = {d^2 \over dt}(\bold r) = \ddot{\bold r}$
Dans le cas d'un mouvement circulaire, chaque point du corps tourne dans un cercle. La position de tout point peut ainsi être décrite par un angle 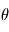$\theta$ par rapport à sa position originelle
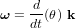
Si $\bold k$ est un vecteur unitaire dans la direction de l'axe de rotation, la vitesse angulaire est alors obtenue par : ${\boldsymbol\omega} = {d \over dt}(\theta) \ \bold k$
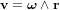
La vitesse linéaire d'un point du corps en rotation s'exprimer alors : $\bold v = \boldsymbol\omega \wedge \bold r$

Dans le cas d'un mouvement circulaire, chaque point du corps tourne dans un cercle.

Cinématique et changement de référentiels

Dans notre domaine, nous sommes constamment contraints de passer d'un repère à un autre pour décrire la trajectoire d'un objet. En cas de référentiels en rotation, tels qu'un référentiel fixé par rapport à la Terre et un référentiel inertiel, passer de l'un à l'autre nécessite d'introduire des termes supplémentaires. Par exemple, si l'on veut décrire la position, la vitesse et l'accélération d'une particule dans un référentiel inertiel noté à partir de sa position dans un référentiel terrestre (fixé par rapport à la Terre) noté 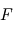, on peut écrire :

$\bold{r}_I = [T]_{I|F} \ \bold{r}_F$
$\bold{v}_I = \frac{d}{dt} (\bold{r}_I) = [T]_{I|F} \ \frac{d}{dt} (\bold{r}_F) + \frac{d}{dt}([T]_{I|F}) \ \bold{r}_F = [T]_{I|F} \ \frac{d}{dt}(\bold{r}_F) + ([T]_{I|F} \ [\Omega]) \ \bold{r}_F$

Nous avons utilisé la dérivée de la MCD qui est introduite dans le chapitre sur la cinématique d'attitude. Finalement :

$\bold{v}_I = [T]_{I/F} ([\Omega] \ \bold{r}_F + \bold{v}_F)$
$\bold{a}_I = \frac{d}{dt}(\bold{v}_I) = \frac{d}{dt}([T]_{I/F}) ([\Omega] \ \bold{r}_F + \bold{v}_F) + [T]_{I/F} \left[ \frac{d}{dt}([\Omega]) \ \bold{r}_F + [\Omega] \ \frac{d}{dt}(\bold{r}_F) + \frac{d}{dt}(\bold{v}_F)\right]$

$\bold{a}_I = [T]_{I/F} \left[ [\Omega] \left([\Omega] \ \bold{r}_F \right) + 2 \ [\Omega] \ \bold{v}_F + \frac{d}{dt}([\Omega] \ \bold{r}_F + \bold{a}_F \right]$

Dans le réferentiel en rotation (celui fixé par rapport à la Terre), la deuxième loi de Newton peut alors être écrite :

$\bold{F}_F = [T]_{F/I} \left( m \ \bold{a}_I \right) = m \left[ [\Omega] \left( [\Omega] \ \bold{r}_F \right) + 2 \ [\Omega] \ \bold{v}_F + \frac{d}{dt}([\Omega]) \ \bold{r}_F + \bold{a}_F \right]$

où $\frac{d}{dt} \left( [\Omega] \right)$ est l'accélération angulaire. On introduit ici les accélérations centripète $[\Omega] \left( [\Omega] \ \bold{r}_F \right)$ et de Coriolis $2 \ [\Omega] \ \bold{v}_F$ .

La simulation et l'estimation d'attitude nécessitent généralement des représentations simples de l'attitude, telles que celles présentées dans le chapitre du même nom. Les équations différentielles de la cinématique peuvent ainsi être obtenues pour ces différentes représentations. Les démonstrations de ces équations sont proposées en exercices.

La cinématique d'attitude relie des vitesses angulaires à des orientations dans l'espace. Si cela peut sembler simple dans le cas d'une rotation autour d'un axe fixe, cela devient beaucoup moins intuitif dans le cas d'un mouvement plus général, où l'axe de rotation varie au cours du temps. 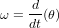Pour un corps en rotation autour d'un axe fixe, l'orientation par rapport à cet axe peut être déterminée en intégrant la vitesse angulaire ω, puisque $\omega = \frac{d}{dt}(\theta)$ .

MCD

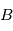Dans le cas général, la matrice exprimant le taux de variation de l'attitude est plus complexe. Considérons un référentiel en rotation par rapport à un référentiel 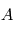avec une vitesse angulaire 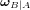$\boldsymbol\omega_{B|A}$ . Si la matrice d'attitude s'exprime $[T]_{B|A}$ , alors :

$\frac{d}{dt} \left( [T]_{B|A} \right) = -[\Omega] \ [T]_{B|A}$ avec $[\Omega] = \begin{pmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{pmatrix}$

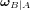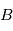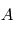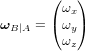La matrice d'attitude se retrouve multipliée par une matrice anti-symétrique qui est définie à partir du vecteur $\boldsymbol\omega_{B|A}$ représentant la vitesse angulaire du référentiel par rapport au référentiel , avec $\boldsymbol\omega_{B|A} = \begin{pmatrix} \omega_x \\ \omega_y \\ \omega_z \end{pmatrix}$ .

Dans ce cas, nous avons utilisé une MCD.

Angles d'Euler

Il est également possible d'exprimer cette équation différentielle en utilisant les angles d'Euler. En reprenant la séquence de rotations $[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3$ conduisant du référentiel 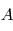au référentiel 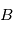l'équation de la cinématique est réécrite :

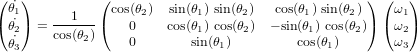
$\begin{pmatrix} \dot{\theta_1} \\ \dot{\theta_2} \\ \dot{\theta_3} \end{pmatrix} = \frac{1}{\textup{cos}(\theta_2)} \begin{pmatrix} \textup{cos}(\theta_2) & \textup{sin}(\theta_1) \ \textup{sin}(\theta_2) & \textup{cos}(\theta_1) \ \textup{sin}(\theta_2) \\ 0 & \textup{cos}(\theta_1) \ \textup{cos}(\theta_2) & -\textup{sin}(\theta_1) \ \textup{cos}(\theta_2) \\ 0 & \textup{sin}(\theta_1) & \textup{cos}(\theta_1) \end{pmatrix} \begin{pmatrix} \omega_1 \\ \omega_2 \\ \omega_3 \end{pmatrix}$

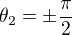En connaissant la vitesse angulaire d'un référentiel par rapport à l'autre en fonction du temps il est possible de déterminer la position au cours du temps d'un référentiel par rapport à l'autre. Néanmoins, l'intégration nécessite le calcul de fonctions trigonométriques ainsi que des singularités (ici $\theta_2 = \pm \frac{\pi}{2}$ ).

Quaternions

Dans le cas des quaternions, l'expression de l'équation de la cinématique se retrouve simplifiée :

$\dot{\bold q} = \begin{pmatrix} \dot{q_0} \\ \dot{q_1} \\ \dot{q_2} \\ \dot{q_3} \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 0 & -\omega_1 & -\omega_2 & -\omega_3 \\ \omega_1 & 0 & \omega_3 & -\omega_2 \\ \omega_2 & -\omega_3 & 0 & \omega_1 \\ \omega_3 & \omega_2 & -\omega_1 & 0 \end{pmatrix} \begin{pmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \end{pmatrix}$

Une écriture plus compacte est possible :

$\begin{cases} \dot{\bold q}_{1:3} = \frac{1}{2} \left(q_0 \ \boldsymbol\omega - \boldsymbol\omega \wedge \bold q_{1:3} \right) \\ \dot{q}_0 = -\frac{1}{2} \ \boldsymbol\omega^T \bold{q}_{1:3} \end{cases}$

Contrairement aux angles d'Euler, les quaternions ne présentent pas de singularité géométrique. L'équation cinématique exprimée avec les quaternions ne possède pas de fonctions trigonométriques, ce qui rend les quaternions parfaitement adaptés aux calculs à bord réalisés en temps réel. Ainsi, les algorithmes de détermination d'attitude modernes sont généralement décrits en termes de quaternions.

Cinématique du satellite

Cinématique du point

Bases de la cinématique

Cinématique et changement de référentiels

Cinématique d'attitude

MCD

Angles d'Euler

Quaternions