Dans cette partie, nous verrons comment s'établit la structure thermique dans les couches externes fluides (principalement gazeuses, ce que l'on appelle les atmosphères) des planètes, ainsi que les conséquences de l'existence d'une telle structure.
 Prérequis
Prérequis
Il est possible de parcourir la partie Découvrir avec un simple bagage de Terminale scientifique ou d'amateur de vulgarisation scientifique. En revanche, la bonne compréhension des phénomènes en jeu et la capacité à calculer même approximativement les conditions moyennes au sein d'une atmosphère planétaire exigent un bagage en physique générale niveau licence, à savoir plus précisément :
- Thermodynamique Connaissance du modèle du gaz parfait, des notions de pression, de température et de chaleur, du lien entre température et énergie cinétique microscopique, de la notion de capacité calorifique et de chaleur latente de changement d'état.
- Mécanique Notions d'énergie cinétique et d'énergie potentielle de pesanteur, connaissance de la loi hydrostatique
- Électromagnétisme Notion de spectre électromagnétique et des principaux domaines de fréquence et longueurs d'onde (visible et infrarouge notamment), de photon. Une connaissance préalable du modèle du corps noir pourra être utile, mais sera introduite dans ce cours et à ce titre n'est pas un prérequis obligatoire.
[Cliquer ici pour commencer le cours]
Conditions à la surface
L'observation de la seule biosphère connue à jour (celle de la Terre) conduit les exobiologistes à poser comme nécessaire la présence d'eau liquide (ou au moins d'un liquide aux propriétés analogues comme l'ammoniac) à la surface d'une planète pour qu'une chimie prébiotique complexe, puis une activité biologique au sens propre, puisse s'y développer. Si bien que la notion d'habitabilité planétaire est de nos jours quasiment devenue un synonyme de présence possible d'eau liquide.
Or, si la disponibilité de l'eau dans l'Univers ne fait guère de doutes (la molécule H2O étant l'une des plus répandues), la question de son apport sur les planètes telluriques fait encore l'objet de débats. Surtout, la permanence de son état liquide est encore plus difficile à obtenir, et nécessite une fourchette de conditions de pression et de température bien particulières (ainsi, à la pression atmosphérique terrestre, doit-on se trouver entre 0°C et 100°C pour que l'eau puisse demeurer liquide). Les conditions de pression et de température au sein des atmosphères planétaires de leur sommet jusqu'à l'éventuelle surface constituent donc l'un des facteurs essentiels conditionnant les phénomènes pouvant s'y dérouler (qu'ils soient de nature biologique, ou plus simplement chimique ou météorologique).
Classification des atmosphères planétaires
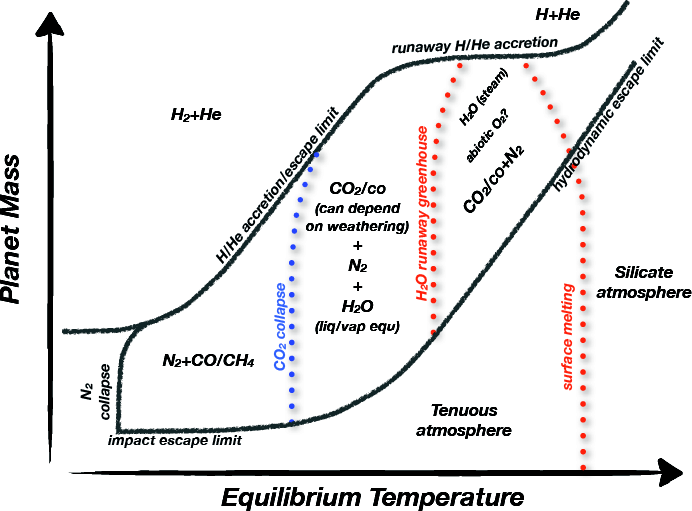
Typologie des atmosphères planétaires en fonction de la température (abscisse) et de la masse de la planète (ordonnée). Les atmosphères habitables correspondent à la zone centrale, où l'eau peut se trouver sous forme de glace, de vapeur et, de façon cruciale, liquide.
Crédit :
Tiré de Forget & Leconte (2013)
Observables à distance
Une autre question cruciale est celle de la détectabilité de telles planètes dans notre voisinage galactique. Le seul moyen envisageable pour caractériser ces planètes consiste en l'étude spectroscopique (c'est-à-dire, décomposé selon ses différentes "couleurs") du rayonnement qui nous parvient. Ce rayonnement peut nous parvenir principalement par deux processus physiques distincts :
- par la réflexion de la lumière (surtout visible) en provenance de l'étoile-hôte. Cette réflexion est fortement influencée par l'atmosphère entourant la planète, et tout particulièrement par les éventuels nuages. Or ces nuages sont constitués de particules solides et/ou liquides en suspension dans l'atmosphère (sur Terre, principalement des gouttes d'eau liquide ou des cristaux de glace d'eau), et ne peuvent être présents que si une telle condensation est possible, d'où l'importance de connaître les conditions de pression et de température au sein de ces atmosphères. De plus, certains composés gazeux peuvent absorber la lumière stellaire réfléchie dans certaines régions du spectre qui leur sont propres, permettant ainsi d'analyser à distance la composition chimique de l'atmosphère.
- par l'émission thermique propre de la planète. Cette émission thermique est conditionnée par les températures des différentes couches de l'atmosphère et de la surface, ainsi que par la capacité de ses constituants à émettre et absorber efficacement ce rayonnement thermique. Son analyse spectroscopique nécessite donc une bonne compréhension des mécanismes en jeu dans cette émission. Ceci permet en retour de pouvoir mesurer à distance la composition et/ou la température au sein d'une atmosphère distante de plusieurs années-lumière...
Il existe trois modes de transport de la chaleur au sein des atmosphères planétaires, qui déterminent les variations de température au sein de ces atmosphères :
- Rayonnement électromagnétique Il s'agit là du seul mode qui puisse opérer à travers le vide. Un objet chaud va se mettre à l'équilibre thermodynamique local avec le champ électromagnétique environnant et lui communiquer une partie de son énergie qui sera rayonnée dans tout l'espace (voir la page traitant du corps noir pour plus de détails). Ce rayonnement pourra être absorbé loin de là par un autre objet qui verra alors son énergie interne (et donc sa température) augmenter. Ce phénomène peut être expérimenté facilement dans la vie de tous les jours (lorsque l'on ressent la chaleur d'un feu de bois alors qu'on est situé à plusieurs mètres de là, hors du trajet des fumées).
- Conduction C'est un mode de transport possible uniquement dans un milieu matériel. L'agitation thermique de la matière se transmet de proche en proche par simple contact (chocs) entre les molécules du milieu. Un exemple de la vie quotidienne serait un couvert métallique touchant une flamme à l'une de ses extrémités. Au bout d'un certain temps, l'autre extrémité sera à température suffisamment élevée pour qu'on ne puisse plus enlever le couvert sans se brûler. Ce mode de transport est surtout efficace à courte distance (comparable à celle entre les molécules et donc au contact), ce qui le rend peu important au sein des atmosphères planétaires (excepté dans les couches très peu denses où les molécules sont loin les unes des autres, et où les autres modes de transport d'énergie sont encore moins efficaces).
- Convection C'est un mode de transport d'énergie qui n'est possible que dans de la matière fluide (ce qui est le cas au sein des atmosphères). La matière elle-même voyage et transporte son énergie interne avec elle, où elle peut être communiquée ensuite par simple contact à la matière environnante (conduction à courte distance). L'exemple caractéristique de la vie quotidienne est le chauffage de l'eau dans une casserole : l'eau est chauffée par conduction avec le fond de la casserole, ce qui entraîne la mise en place d'une circulation de liquide (courants de convection) permettant à cette chaleur d'être distribuée à l'ensemble de l'eau de la casserole de façon homogène.
Illustration des modes de transport de la chaleur
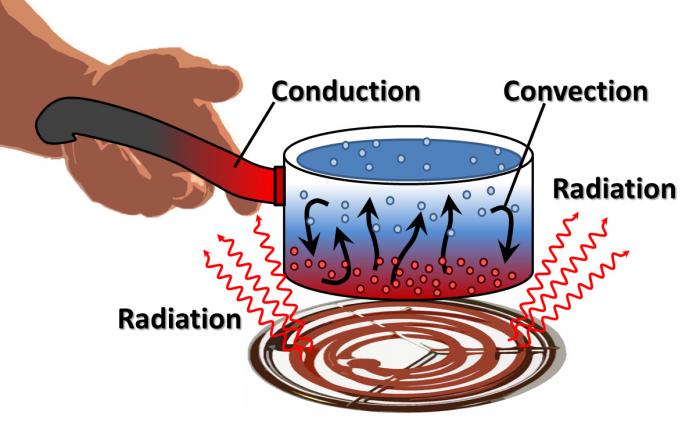
Dans cette situation de la vie quotidienne, les trois modes de transport de l'énergie sont illustrés : la chaleur (énergie thermique) voyage au sein du liquide par des mouvement de convection, la casserole est chauffée radiativement par la plaque et le manche métallique est un bon conducteur de chaleur vers la main.
 Définition et intérêt
Définition et intérêt
Une des plus importantes caractéristiques des atmosphères planétaires est leur épaisseur verticale. En toute rigueur, leur densité décroît continûment avec l'altitude jusqu'à rejoindre celle du milieu interplanétaire, si bien qu'il est difficile de leur attribuer une épaisseur bien définie. On peut néanmoins caractériser la rapidité avec laquelle cette densité décroît avec l'altitude (atmosphère plus ou moins bien "tassée" verticalement). Cela définit ce que l'on appelle l'échelle de hauteur atmosphérique, qui représente la différence d'altitude entraînant une division de la pression atmosphérique (liée à la densité) par un facteur constant (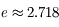 ). Le lecteur intéressé par une définition quantitative pourra se reporter ici.
). Le lecteur intéressé par une définition quantitative pourra se reporter ici.
Facteurs influant sur l'échelle de hauteur
Cette échelle de hauteur est le résultat du compromis entre deux phénomènes physiques : la gravitation qui tend à tasser les molécules de l'atmosphère vers le bas, et l'agitation thermique des molécules qui tend à les disperser dans tout l'espace, y compris vers le haut. À ce titre, et toutes choses égales par ailleurs, l'échelle de hauteur atmosphérique est :
- d'autant plus grande que la température de l'atmosphère est élevée.
- d'autant plus petite que la gravité de la planète est élevée ou le gaz constituant l'atmosphère est dense.
Échelles de hauteur des atmosphères du système solaire
| Planète (ou satellite) | Vénus | Terre | Mars | Jupiter | Io | Saturne | Titan | Uranus | Neptune | Triton | Pluton |
|---|
| Échelle de hauteur (en km) | 16 | 8,4 | 11 | 25 | 7,9 | 48 | 21 | 27 | 22 | 14 | 18 |
Dans le système solaire, les valeurs extrêmes vont de  pour la Terre à environ
pour la Terre à environ  pour Saturne. Ces valeurs sont en général très petites devant le rayon de la planète, si bien que l'on peut négliger la courbure de la planète et considérer l'atmosphère comme une succession de couches planes empilées de bas en haut. C'est ce que l'on appelle l'approximation plan-parallèle.
pour Saturne. Ces valeurs sont en général très petites devant le rayon de la planète, si bien que l'on peut négliger la courbure de la planète et considérer l'atmosphère comme une succession de couches planes empilées de bas en haut. C'est ce que l'on appelle l'approximation plan-parallèle.
Détermination graphique de l'échelle de hauteur
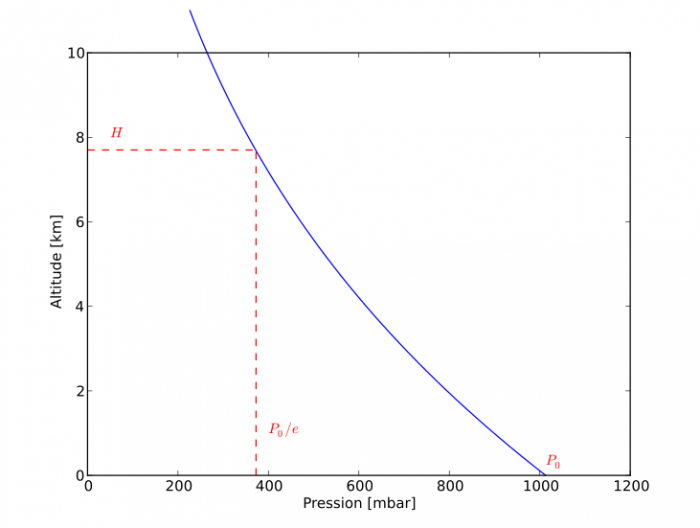
Lecture graphique de l'échelle de hauteur atmosphérique. Sur le profil de pression standard de l'atmosphère terrestre, on repère l'altitude
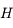
à laquelle la pression est divisée par le nombre
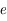
(environ 2,718). Cette altitude définit l'échelle de hauteur au niveau de la surface, proche ici de

.
Crédit :
Emmanuel Marcq
 Définition
Définition
Là où la convection est le mode de transport dominant d'énergie dans une atmosphère, on constate une décroissance régulière de la température avec l'altitude selon un coefficient (en °C/km ou K/km) appelé gradient adiabatique. En effet, si l'on considère une masse de gaz au cours de son transport dans un courant de convection vertical, celle-ci devra lutter contre la pesanteur et donc fournir de l'énergie pour ce faire. Or, le seul "réservoir" d'énergie d'un gaz parfait réside dans sa capacité calorifique. Il y aura donc une conversion partielle de son énergie thermique (en fait, de son enthalpie puisqu'on y inclut le travail des forces de pression) vers de l'énergie potentielle de pesanteur, et donc une baisse de la température de la parcelle d'air d'autant plus grande que celle-ci aura acquis davantage d'altitude (voir ici pour la démonstration). Si une région de l'atmosphère est soumise à cette circulation et en négligeant les autres modes de transport d'énergie, la température y décroît alors avec l'altitude en suivant ce gradient adiabatique.
Gradient adiabatique humide
En pratique cependant, les atmosphères planétaires ne sont pas constituées que de gaz parfaits, mais comportent des gaz en équilibre avec leur propre phase condensée (liquide ou solide). C'est le cas par exemple sur Terre de la vapeur d'eau qui constitue une proportion variable de l'atmosphère terrestre et se trouve parfois en équilibre avec des gouttes d'eau liquide ou des cristaux de glace d'eau. Ou encore de Titan où c'est le méthane gazeux qui se trouve parfois au contact de gouttes de méthane liquide. En ce cas, il existe un réservoir d'énergie supplémentaire pour une parcelle d'atmosphère en mouvement ascendant, à savoir l'énergie libérée par le gaz condensable lorsqu'il se convertit en gouttelettes liquides ou en cristaux solides, ce que l'on appelle la chaleur latente de condensation. Ce réservoir supplémentaire d'énergie limite alors la baisse de température avec l'altitude vers une valeur plus faible. On parle alors de gradient adiabatique humide, que l'on distingue du gradient adiabatique sec en l'absence de condensation.
Troposphère
La couche atmosphérique où la convection est le mode dominant de transport d'énergie s'appelle la troposphère, caractérisée par la décroissance en température décrite ci-dessus. C'est la couche atmosphérique la plus profonde, au contact de la surface pour les planètes telluriques. Au-dessus de la troposphère, les densités plus faibles rendent le transport d'énergie par rayonnement comparativement plus efficace que la convection, car le milieu dilué devient davantage transparent au rayonnement thermique.
Comparaison des profils thermiques de la Terre et de Titan
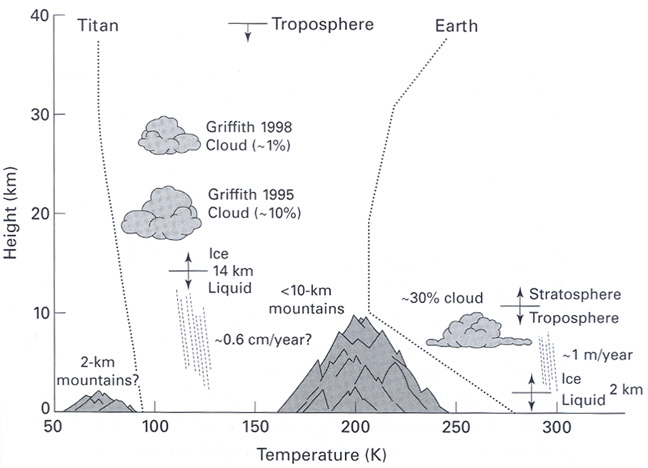
Comparaison des profils thermiques des atmosphères de la Terre et de Titan (un satellite de Saturne). On y constate que le profil thermique y suit une pente constante entre la surface et 10 km d'altitude pour la Terre et 30 km pour Titan, ce qui définit l'étendue verticale de la troposphère pour les deux atmosphères. Ces pentes correspondant aux gradients adiabatiques, plus fort sur Terre que sur Titan car la gravité terrestre est plus forte.
Crédit :
LASP, Université du Colorado
 Définition
Définition
Le corps noir est un objet physique idéal qui absorbe tout le rayonnement électromagnétique qu'il reçoit (sa réflectivité est donc nulle à toutes les longueurs d'onde).
Corps noirs approchés
Certains objets réels sont de bonnes approximations du corps noir idéal, du moins sur certains intervalles de longueur d'onde et dès que le rayonnement réfléchi y est négligeable devant l'émission thermique et en l'absence de processus d'émission autres que thermiques. C'est par exemple le cas de la plupart des objets du quotidien dans le domaine infrarouge moyen (pour les longueurs d'onde autour de 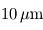 .), ou encore des étoiles dans le domaine visible.
.), ou encore des étoiles dans le domaine visible.
Spectres de corps noir
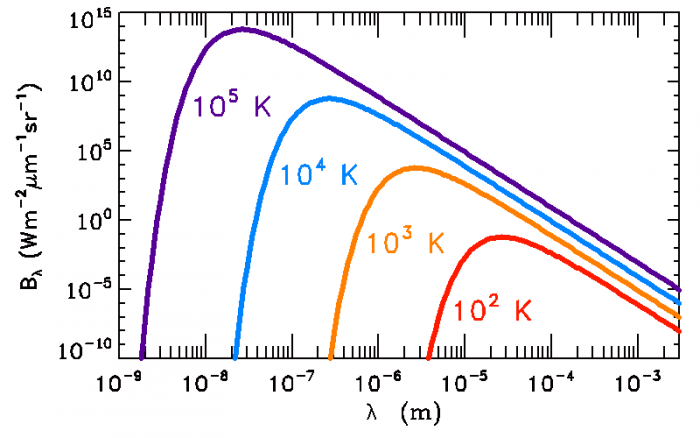
Représentation des spectres thermiques émis par divers corps noir de température variable. Notez les échelles logarithmiques utilisées sur chacun des axes, nécessaires pour bien représenter les longueurs d'onde du pic et puissances spectrales, toutes deux très différentes selon la température.
Crédit :
Astrophysique sur Mesure
Domaines visibles et infrarouge thermique
Il est d'usage de distinguer deux intervalles spectraux différents lorsque les planètes ont une température notablement plus faible que leur étoile (ce qui est toujours le cas dans le système solaire, mais pas toujours pour les planètes extrasolaires !).
- Domaine UV-visible-proche IR C'est dans ces longueurs d'onde que la grande majorité de la puissance stellaire est émise. Cela recouvre en général l'UV, le visible et une partie du proche infrarouge (inférieure à
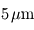 ).
). - Domaine infrarouge thermique C'est le domaine de longueurs d'onde où les planètes émettent l'immense majorité de leur puissance. Cela concerne les longueurs d'onde supérieures à
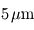 et jusqu'à quelques dizaines de micromètres (d'autant plus que la planète est froide).
et jusqu'à quelques dizaines de micromètres (d'autant plus que la planète est froide).
 Définition
Définition
La température d'équilibre d'une planète est la température théorique de sa surface (si on suppose cette température uniforme) en l'absence d'atmosphère. C'est une grandeur théorique qui n'a pas vocation à être mesurée, contrairement à la température effective.
Bilan de rayonnement
La température d'équilibre se détermine à partir d'un simple bilan de rayonnement (visible et thermique). Cela revient à négliger les autres sources d'énergie que le rayonnement de l'étoile hôte (le Soleil pour la Terre par exemple) : géothermie, réactions chimiques ou nucléaires, transitions de phase, etc. Sont pris en compte :
- Rayonnement reçu Il s'agit du rayonnement en provenance de l'étoile hôte. Il n'arrive que sur la face éclairée de la planète (côté jour), avec une inclinaison variable.
- Rayonnement réfléchi C'est la part du rayonnement reçu par la planète qui est renvoyé vers l'espace. Le rapport entre la puissance reçue et la puissance réfléchie porte le nom d'albédo bolométrique.
- Rayonnement thermique Il est émis par la totalité de la surface planétaire (côtés jour et nuit) qui se comporte en excellente approximation comme un corps noir dans l'infrarouge thermique. Ce rayonnement dépend donc de la température de surface.
La température de surface influe ici sur le rayonnement thermique. Elle est égale à la température d'équilibre lorsque le bilan est équilibré, à savoir : Puissance lumineuse reçue = Puissance lumineuse réfléchie + Puissance rayonnée thermiquement, ce qui est équivalent à Puissance lumineuse absorbée = Puissance rayonnée thermiquement.
Détermination de la température d'équilibre

Bilan de puissance pour une planète sans atmosphère : le flux reçu de l'étoile équilibre la somme du flux réfléchi par la planète et du flux rayonné thermiquement (en rouge), qui dépend fortement de la température de la planète. Ce bilan peut donc servir à déterminer cette température, appelée température d'équilibre.
Crédit :
Emmanuel Marcq
Influence des différents paramètres
- Taille de la planète Elle n'influe pas sur la température d'équilibre : les puissances reçues, réfléchies et rayonnées thermiquement varient toutes de façon proportionnelle à la surface de la planète, qui n'a donc pas d'influence sur la température d'équilibre.
- Puissance rayonnée par l'étoile Toutes choses égales par ailleurs, la température d'équilibre croît avec la puissance totale rayonnée par l'étoile (l'étoile pouvant être considérée comme un corps noir, cette puissance totale dépend de la température à la surface de l'étoile et du rayon de l'étoile).
- Distance entre l'étoile et la planète À puissance rayonnée par l'étoile donnée, une planète capte une proportion plus importante de ce rayonnement si elle se trouve à proximité de l'étoile, comme on pouvait s'y attendre.
- Albédo de la planète Un albédo élevé signifie que la planète absorbe une plus faible partie du rayonnement stellaire incident, ce qui tend à diminuer la température d'équilibre. Ainsi, la température d'équilibre de la Terre est plus élevée que celle de Vénus bien qu'elle reçoive environ deux fois moins de puissance solaire, car l'albédo de Vénus très élevé résulte en une puissance solaire absorbée moindre pour Vénus.
Une remarque importante est que cette définition repose sur l'hypothèse irréaliste d'une température de surface homogène sur l'ensemble de la planète, donc avec une redistribution parfaite de l'énergie. Cette température est donc un outil théorique plus qu'une température physiquement mesurable. Le lecteur intéressé par une approche plus quantitative (mais identique conceptuellement) pourra se reporter ici.
 Définition
Définition
La température effective est une mesure de la puissance émise thermiquement par une planète. Elle se définit comme la température du corps noir (idéal) émettant la même puissance totale (en comptant toutes les longueurs d'onde) que la planète par unité de surface. Contrairement à la température d'équilibre, c'est une grandeur expérimentalement mesurable.
Comparaison entre température effective et température d'équilibre
Nous connaissons assez bien le système solaire pour pouvoir mesurer les températures effectives des planètes et les comparer aux températures d'équilibre théoriques. Le résultat est résumé sur le tableau ci-dessous :
Températures caractéristiques dans le système solaire
| Planète (ou satellite) | Mercure | Vénus | Terre | Lune | Mars | Jupiter | Saturne | Titan | Uranus | Neptune |
|---|
| Température d'équilibre (°C) | 161 | -42 | -19 | -2 | -63 | -163 | -192 | -191 | -215 | -227 |
| Température effective (°C) | 161 | -42 | -19 | -2 | -63 | -149 | -178 | -191 | -214 | -214 |
| Température moyenne de surface (°C) | 161 | 462 | 15 | -2 | -58 | N/A | N/A | -179 | N/A | N/A |
Pour la plupart des planètes extrasolaires (hormis les plus grosses et les plus chaudes), seule la température d'équilibre peut être estimée (en supposant un albédo donné par un modèle théorique). Les ordres de grandeur de ces deux températures sont comparables lorsque la source d'énergie principale de l'atmosphère est le rayonnement de l'étoile hôte, comme c'est le cas dans le système solaire. Pour les planètes telluriques (et le satellite de Saturne Titan), ces deux températures sont mêmes égales car les sources d'énergie interne à la planète ont un effet négligeable sur l'atmosphère, ce qui n'est pas le cas pour les géantes gazeuses.
Comparaison entre température effective et température de surface
On constate également sur le tableau précédent que pour les corps possédant une surface solide, la température moyenne de la surface est toujours au moins égale à la température effective (égale pour un corps sans atmosphère comme la Lune ou bien Mercure, supérieure pour ceux possédant une atmosphère). Ce phénomène est appelé effet de serre et sera expliqué plus en détail à la page suivante.
 Origine
Origine
Le phénomène essentiel à l'origine de l'effet de serre au sein d'une atmosphère réside dans la différence d'absorption des rayonnements infrarouge thermique (en provenance de la planète) et visible/UV (en provenance de l'étoile) par les constituants de l'atmosphère. Les constituants gazeux d'une atmosphère (en excluant les particules solides ou liquide en suspension comme les poussières ou les cristaux et gouttelettes des nuages) sont en général transparents pour la lumière visible émise par leur étoile. En revanche, certains de ces gaz (comme la vapeur d'eau H2O, le dioxyde de carbone CO2 ou encore le méthane CH4) absorbent très bien le rayonnement infrarouge d'origine thermique émis par la planète.
Mécanisme
Cette différence d'absorption entre les rayonnements conduit à une séparation entre les régions :
- où l'énergie rayonnée en provenance de l'étoile (en visible) est absorbée : au niveau de la surface pour les planètes telluriques, dans l'atmosphère profonde pour les planètes géantes.
- où l'énergie rayonnée en provenance de la planète (en infrarouge) est émise vers l'espace. Ce rayonnement thermique infrarouge est émis à une altitude d'autant plus élevée que l'atmosphère est opaque aux infrarouges : il faut que les couches émettrices puissent rayonner directement vers l'espace.
Or, le bilan d'énergie de la planète impose que ce soit la couche rayonnant vers l'espace qui soit à la température effective permettant un équilibre entre la puissance reçue et celle absorbée. Il faut donc que l'énergie absorbée en profondeur puisse être transportée jusqu'à cette altitude de rayonnement. Comme l'atmosphère profonde située entre ces deux niveaux est opaque aux infrarouges, le rayonnement n'est pas le mode le plus efficace de transport, et c'est la convection qui prend le relais. Cette atmosphère profonde, s'étendant depuis l'altitude d'émission infrarouge jusqu'en bas (surface ou intérieur planétaire pour les géantes) n'est autre que la troposphère définie précédemment. Afin que ce transport d'énergie par convection puisse avoir lieu, il faut que la température de surface soit plus élevée que celle au sommet de la troposphère selon le gradient adiabatique. La température au sommet de la troposphère étant égale à la température effective, la température de surface est en conséquence plus élevée, ce qui est la définition même de l'effet de serre.
Effet de serre et profil thermique
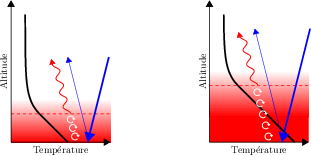
Effet de serre modéré (à gauche) et intense (à droite). L'augmentation de l'opacité infrarouge de l'atmosphère (à droite) force le rayonnement thermique à provenir de couches plus élevées (à partir du pointillé rouge). La troposphère, zone où la convection assure le transport d'énergie vers le haut (flèches blanches) et où le profil de température est linéaire, s'étend donc plus profondément. Cela conduit à une température de surface plus élevée : l'effet de serre a augmenté (mais le profil de température dans la zone supérieure radiative reste inchangé ! Le bilan radiatif global et donc la température effective restent identiques.)
Crédit :
Emmanuel Marcq
Ce sont les couches atmosphériques situées au-dessus de la troposphère, où la convection joue un rôle négligeable.
 Mésosphère
Mésosphère
La couche atmosphérique située au-dessus de la troposphère est (en général, voir page suivante) appelée mésosphère. Le transport d'énergie s'y fait exclusivement par rayonnement. La température y décroît avec l'altitude en tendant vers une valeur appelée température de peau atmosphérique. Cette décroissance s'y effectue de façon beaucoup plus modérée que dans la troposphère située en dessous et soumise au gradient adiabatique.
 Thermosphère
Thermosphère
Au sommet de la mésosphère, l'atmosphère devient complètement transparente à tous les rayonnements (les rayonnements visible ou IR thermique ne peuvent donc y déposer leur énergie) et extrêmement ténue (la convection est donc inefficace). Le transport d'énergie y est donc assuré faute de mieux par des processus de conduction qui sont eux-mêmes très inefficaces à grande distance. Cette zone connaît donc d'énormes contrastes de température verticaux et horizontaux car l'énergie qui y est déposée par les particules énergétiques de l'espace interplanétaire ou les rayonnements X et γ de l'étoile s'évacue très difficilement, ce qui conduit à l'appellation de thermosphère. La température y croît avec l'altitude, comme montré plus en détail ici.
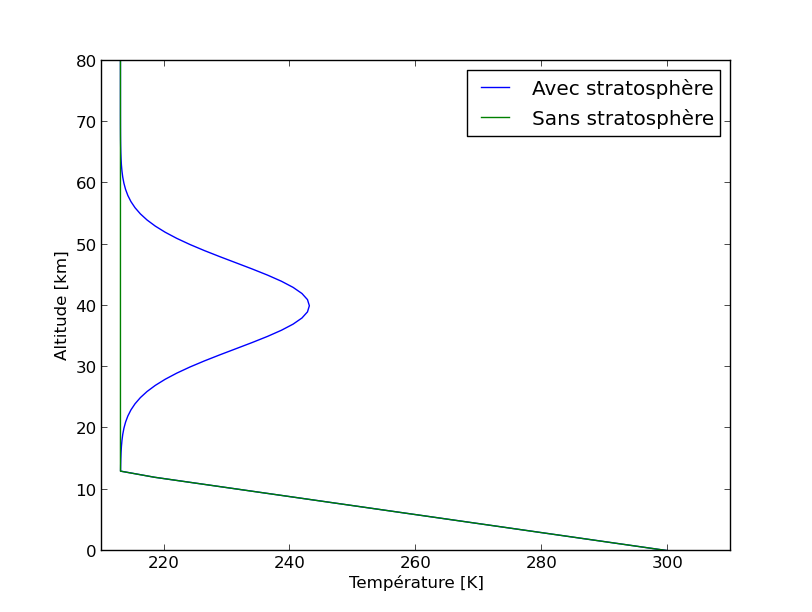
 Stratosphère
Stratosphère
Certaines atmosphères planétaires possèdent une couche supplémentaire appelée stratosphère située entre la troposphère et la mésosphère. Cette couche est une couche radiative (la convection n'y joue aucun rôle dans le transport vertical de la chaleur) et connaît une inversion de température : la température y croît avec l'altitude ! Cette inversion est causée par une absorption partielle de la lumière et/ou des UV stellaires assez haut dans l'atmosphère, si bien que cette énergie ne peut pas s'évacuer par convection et seulement difficilement par radiation. Il se crée alors une anomalie chaude qui déforme le profil de température, allant jusqu'à l'inversion de température.
Dans le système solaire, Vénus et Mars ne possèdent pas de stratosphère (ces atmosphères principalement constituées de CO2 rayonnent très efficacement en infrarouge le peu de puissance absorbé à haute altitude, si bien que les anomalies de températures n'altèrent pas la forme du profil thermique). La Terre en possède une, causée par l'absorption des UV solaires par l'ozone (O3), sous-produit du dioxygène (O2) d'origine biologique. Les planètes géantes en possèdent également (causée par des composés hydrocarbonés absorbant les UV) ainsi que Titan (par absorption des UV solaires sur les particules du brouillard photochimique produit dans la haute atmosphère).
Profils thermiques des trois atmosphères telluriques du système solaire
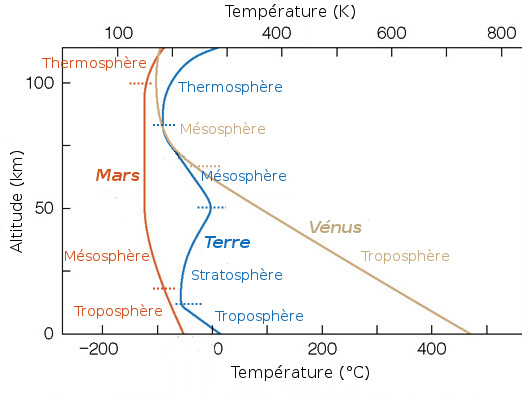
Profils thermiques de Mars, Vénus et de la Terre. Les profils thermiques des atmosphères de Mars et de Vénus ne comportent pas de stratosphère, tandis que l'atmosphère terrestre en comporte une, située d'après ce graphique entre 10 et 50 km d'altitude.
Crédit :
Laboratory for Atmospheric and Space Physics, traduit et adapté par E. Marcq
Nous allons à présent aborder les lois quantitatives permettant de modéliser simplement les profils verticaux de température au sein des atmosphères planétaires. Cela nécessite quelques rappels sur le rayonnement thermique, dit de "corps noir".
 Loi de Wien
Loi de Wien
Elle donne la position du maximum en 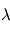 de
de 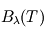 à température
à température 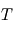 donnée, comme illustré précédemment.
donnée, comme illustré précédemment.
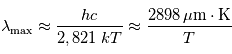
Autrement dit, plus le corps est chaud, et plus il émet principalement à des longueurs d'ondes courtes et ce de façon inversement proportionnelle. Cela justifie la séparation du spectre lumineux en :
- lumière UV-visible-proche IR : émise par les objets d'une température de quelques milliers de Kelvins. Ainsi, pour le Soleil,
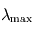 est voisin de
est voisin de 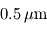 (soit dans le vert).
(soit dans le vert). - infrarouge thermique : émis par les objets d'une température de quelques dizaines à quelques centaines de Kelvins, comme les planètes du système solaire. Ainsi, pour la Terre,
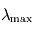 est voisin de
est voisin de 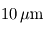 .
.
La séparation entre les deux domaines est prise de façon conventionnelle autour de 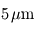 . Dans le contexte exoplanétaire, une remarque importante s'impose dès maintenant : la plupart des exoplanètes actuellement connues sont extrêmement chaudes, avec des températures excédant souvent
. Dans le contexte exoplanétaire, une remarque importante s'impose dès maintenant : la plupart des exoplanètes actuellement connues sont extrêmement chaudes, avec des températures excédant souvent 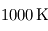 , si bien que la limite entre infrarouge thermique et lumière stellaire est décalée vers de plus courtes longueurs d'onde, voire devient complètement dénuée de sens. Cela empêche notamment d'appliquer tels quels les modèles atmosphériques conçus dans le système solaire qui distinguent ces deux catégories.
, si bien que la limite entre infrarouge thermique et lumière stellaire est décalée vers de plus courtes longueurs d'onde, voire devient complètement dénuée de sens. Cela empêche notamment d'appliquer tels quels les modèles atmosphériques conçus dans le système solaire qui distinguent ces deux catégories.
 Conséquences
Conséquences
- Comme l'absorbance est comprise entre
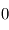 et
et  quelle que soit la longueur d'onde, l'émissivité l'est aussi. Il en résulte qu'aucun corps ne peut rayonner plus efficacement que le corps noir à longueur d'onde et température donnée.
quelle que soit la longueur d'onde, l'émissivité l'est aussi. Il en résulte qu'aucun corps ne peut rayonner plus efficacement que le corps noir à longueur d'onde et température donnée. - Le corps noir ayant par définition une émissivité constante avec la longueur d'onde et égale à
 , son absorbance est aussi égale à l'unité quelle que soit la longueur d'onde, ce qui justifie son nom de corps noir au sens où il ne réfléchit aucun rayonnement incident.
, son absorbance est aussi égale à l'unité quelle que soit la longueur d'onde, ce qui justifie son nom de corps noir au sens où il ne réfléchit aucun rayonnement incident. - À l'inverse, un réflecteur parfait qui n'absorberait aucun rayonnement serait également dans l'impossibilité d'émettre quelque rayonnement thermique que ce soit. Une application dans la vie courante de ce phénomène est l'aspect métallique et réfléchissant des objets traités pour éviter les pertes thermiques radiatives : couvertures de survie, bouteilles Thermos : en augmentant leur réflectivité, on abaisse leur absorbance, et donc leur émissivité aussi.
Cette page développe de façon quantitative les notions vues de façon qualitative ici.
 Détermination du flux incident sur la planète
Détermination du flux incident sur la planète
- Puissance lumineuse émise par l'étoile : elle s'obtient au moyen de la loi de Stefan-Boltzmann, de la température et de la superficie de la photosphère de l'étoile (sa "surface" visible) :
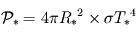
- Flux reçu au niveau de l'orbite de la planète : en supposant le milieu interplanétaire transparent, la puissance émise par l'étoile se dilue (mais sans absorption) sur des sphères concentriques à l'étoile de plus en plus grandes. En notant
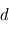 la distance de l'étoile à la planète, on obtient alors un flux (puissance par unité de surface réceptrice)
la distance de l'étoile à la planète, on obtient alors un flux (puissance par unité de surface réceptrice) 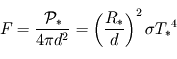
 Bilan de puissance
Bilan de puissance
- Puissance reçue par la planète : l'étoile étant en général assez éloignée de la planète (
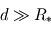 ), les rayons qu'elle émet peuvent être considérés comme parallèles. La façon la plus simple de calculer cette puissance reçue consiste donc à multiplier le flux
), les rayons qu'elle émet peuvent être considérés comme parallèles. La façon la plus simple de calculer cette puissance reçue consiste donc à multiplier le flux 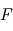 par la surface interceptant toute la lumière reçue par la planète à angle droit des rayons. Cette surface consiste donc ici en un disque du rayon
par la surface interceptant toute la lumière reçue par la planète à angle droit des rayons. Cette surface consiste donc ici en un disque du rayon 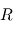 de la planète, d'où
de la planète, d'où 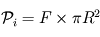
- Puissances réfléchies et absorbées par la planète : en vertu de la définition de l'albédo bolométrique
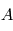 , la proportion réfléchie de la puissance incidente, la partie absorbée représente donc le complémentaire, soit
, la proportion réfléchie de la puissance incidente, la partie absorbée représente donc le complémentaire, soit 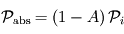 .
. - Puissance rayonnée thermiquement par la planète : en supposant que la surface de la planète à une température uniforme
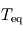 se comporte comme un corps noir aux longueurs d'ondes considérées, cette puissance rayonnée vaut alors
se comporte comme un corps noir aux longueurs d'ondes considérées, cette puissance rayonnée vaut alors 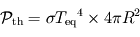 puisque l'ensemble de la planète rayonne.
puisque l'ensemble de la planète rayonne.
 Expression de la température d'équilibre
Expression de la température d'équilibre
Le bilan radiatif à l'équilibre imposant l'égalité entre la puissance rayonnée par la planète et la puissance absorbée par la planète, on obtient alors l'équation suivante :
![\[ \pi R^2 \left(1 - A \right) F = 4 \pi R^2 \sigma {T_{\mathrm{eq}}^4 \]](../pages_fluide-temperature/equations_fluide-temperature-comprendre-noatm/equation50.png)
qui se résout directement, après simplification du rayon 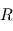 de la planète (ce qui signifie qu'en première approximation, la température d'une planète ne dépend pas de sa taille) en :
de la planète (ce qui signifie qu'en première approximation, la température d'une planète ne dépend pas de sa taille) en :
![T_{\mathrm{eq}} = \left[ \frac{\left(1 - A\right) F}{4 \sigma} \right]^{1/4} = \sqrt{\frac{R_*}{d}} \left( \frac{1-A}{4} \right)^{1/4} T_*](../pages_fluide-temperature/equations_fluide-temperature-comprendre-noatm/equation52.png)
ce qui permet de constater que cette température décroît avec la distance à l'étoile, et est proportionnelle à celle de l'étoile. Ainsi, toutes choses égales par ailleurs, pour une étoile naine rouge d'une température moitié de celle du Soleil, il faut pour conserver une température d'équilibre donnée se rapprocher de l'étoile d'un facteur quatre : on peut d'ores et déjà affirmer que les zones habitables autour des petites étoiles de faible température (naines rouges) sont très proches de ces dernières. Notons au passage que la température d'équilibre d'une planète est bornée par celle de son étoile, plus précisément comprise entre 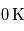 (à très grande distance) et
(à très grande distance) et 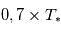 à la limite où l'orbite de la planète est tangente à son étoile (et la planète de rayon négligeable devant l'étoile).
à la limite où l'orbite de la planète est tangente à son étoile (et la planète de rayon négligeable devant l'étoile).
Bilans de flux
Représentation des flux rayonnants
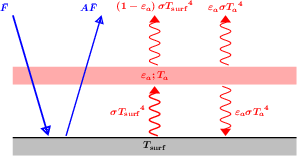
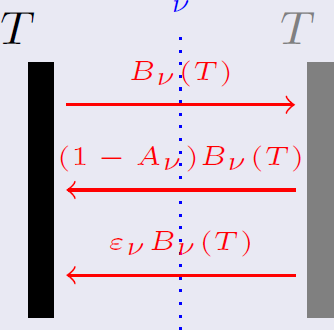
Représentation schématique des flux (bleu pour le domaine stellaire visible-UV-proche IR, rouge pour le domaine infrarouge thermique).
Crédit :
Emmanuel Marcq
La situation est très simple pour les flux stellaires. 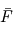 désigne le flux moyen à la surface de la planète, qui se déduit du flux à incidence normale appelé constante solaire (ou stellaire) par l'égalité des puissances :
désigne le flux moyen à la surface de la planète, qui se déduit du flux à incidence normale appelé constante solaire (ou stellaire) par l'égalité des puissances : 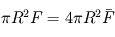 (voir le raisonnement définissant la température d'équilibre pour plus de détails,
(voir le raisonnement définissant la température d'équilibre pour plus de détails, 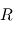 désigne ici le rayon planétaire). On en déduit immédiatement
désigne ici le rayon planétaire). On en déduit immédiatement 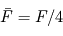 : un facteur 2 s'explique aisément par le fait que seul un hémisphère est éclairé, et l'autre facteur 2 par la moyenne du cosinus de l'angle d'incidence intervenant dans le calcul local du flux.
: un facteur 2 s'explique aisément par le fait que seul un hémisphère est éclairé, et l'autre facteur 2 par la moyenne du cosinus de l'angle d'incidence intervenant dans le calcul local du flux.
En vertu de la définition de l'émissivité, l'atmosphère rayonne donc 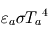 dans chacun des demi-espaces inférieur (vers la surface) et supérieur (vers l'espace). En vertu de la loi de Kirchhoff, cette émissivité est égale à son absorbance, si bien que la fraction complémentaire
dans chacun des demi-espaces inférieur (vers la surface) et supérieur (vers l'espace). En vertu de la loi de Kirchhoff, cette émissivité est égale à son absorbance, si bien que la fraction complémentaire 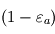 du rayonnement en provenance de la surface (considérée comme un corps noir) réussit à la traverser, le reste étant absorbé (on néglige les processus de diffusion ici ; seules les émissions et absorptions sont prises en compte).
du rayonnement en provenance de la surface (considérée comme un corps noir) réussit à la traverser, le reste étant absorbé (on néglige les processus de diffusion ici ; seules les émissions et absorptions sont prises en compte).
Le bilan des flux à la surface donne alors à l'équilibre radiatif (synonyme d'égalité entre la somme des flux entrants et la somme des flux sortants) : 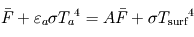 , tandis que celui au niveau de la couche atmosphérique donne
, tandis que celui au niveau de la couche atmosphérique donne 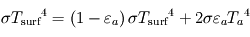 . Nous avons donc deux équations pour les deux inconnues
. Nous avons donc deux équations pour les deux inconnues 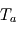 et
et 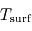 , et la résolution du système donne alors :
, et la résolution du système donne alors : 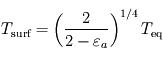 et
et 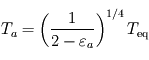 où l'on aura reconnu la température d'équilibre
où l'on aura reconnu la température d'équilibre ![T_{\mathrm{eq}} = \left[\frac{(1-A) F}{4 \sigma} \right]^{1/4} = \left[\frac{(1-A) \bar{F}}{\sigma} \right]^{1/4}](../pages_fluide-temperature/equations_fluide-temperature-comprendre-structure/equation51.png) définie précédemment.
définie précédemment.
 Discussion
Discussion
- Dans la limite transparente où
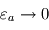 ,
, 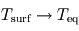 et
et 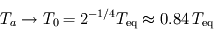 : la surface retrouve alors la température d'équilibre, ce qui est normal pour une atmosphère à la fois transparente en lumière stellaire et en infrarouge thermique (atmosphère radiativement inerte ne causant aucun effet de serre). La température atmosphérique tend alors vers une valeur
: la surface retrouve alors la température d'équilibre, ce qui est normal pour une atmosphère à la fois transparente en lumière stellaire et en infrarouge thermique (atmosphère radiativement inerte ne causant aucun effet de serre). La température atmosphérique tend alors vers une valeur 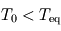 appelée température de peau et typique des couches quasi-transparentes en approximation grise.
appelée température de peau et typique des couches quasi-transparentes en approximation grise. - Dans la limite opaque où
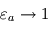 ,
, 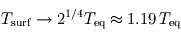 et
et 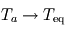 : le rayonnement s'échappant vers l'espace provient alors uniquement de l'atmosphère, qui se met donc à la température d'équilibre. La surface reçoit donc du rayonnement infrarouge atmosphérique en plus du seul rayonnement stellaire (qui pris isolément la maintiendrait déjà à une température de
: le rayonnement s'échappant vers l'espace provient alors uniquement de l'atmosphère, qui se met donc à la température d'équilibre. La surface reçoit donc du rayonnement infrarouge atmosphérique en plus du seul rayonnement stellaire (qui pris isolément la maintiendrait déjà à une température de 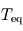 ), si bien que sa température s'élève : c'est ce que l'on appelle l'effet de serre, plafonnant dans ce modèle à une seule couche atmosphérique isotherme à une augmentation de la température absolue (mesurée en Kelvins) de
), si bien que sa température s'élève : c'est ce que l'on appelle l'effet de serre, plafonnant dans ce modèle à une seule couche atmosphérique isotherme à une augmentation de la température absolue (mesurée en Kelvins) de 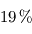 .
.
Modèles à plusieurs couches
Une première idée est d'ajouter, au-dessus de la première couche atmosphérique complètement opaque au rayonnement thermique de la planète, une ou plusieurs couches (la dernière couche immédiatement avant l'espace pouvant être partiellement transparente). Ces différentes couches atmosphériques peuvent alors chacune adopter des températures différentes, et former ainsi un profil de température décroissant avec l'altitude. Il faut ainsi environ une centaine de couches opaques pour rendre compte de la température de surface de Vénus.
L'étude d'un modèle à deux couches atmosphériques fait l'objet du mini-projet associé à ce chapitre.
Modèles radiatifs continus
Une vision plus réaliste mais ne faisant toujours intervenir que des échanges d'énergie par rayonnement consiste à découper l'atmosphère en un mille-feuille constitué d'une infinité de couches atmosphériques infiniment fines (d'un point de vue radiatif). En restant dans l'approximation grise en infrarouge thermique et transparente en lumière visible, il est même possible (mais hors-programme au niveau licence) de démontrer l'expression du profil de température en fonction de la profondeur optique 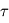 en infrarouge thermique :
en infrarouge thermique : 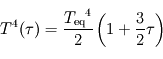 . Notons que dans ce modèle, on obtient
. Notons que dans ce modèle, on obtient 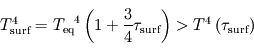 : le seul équilibre radiatif tend à créer une discontinuité de température au niveau de la surface, ce qui déclencherait alors des processus de convection pour y remédier. Un tel contraste thermique est néanmoins observable à la surface des planètes telluriques éclairées par le Soleil, comme une plage sur Terre par beau temps (le sable peut alors être brûlant et l'air frais), ou mieux encore dans les déserts de Mars.
: le seul équilibre radiatif tend à créer une discontinuité de température au niveau de la surface, ce qui déclencherait alors des processus de convection pour y remédier. Un tel contraste thermique est néanmoins observable à la surface des planètes telluriques éclairées par le Soleil, comme une plage sur Terre par beau temps (le sable peut alors être brûlant et l'air frais), ou mieux encore dans les déserts de Mars.
Néanmoins, dans les atmosphères épaisses ou pour expliquer l'existence des stratosphères, l'absorption de la lumière stellaire par l'atmosphère doit être prise en compte (par exemple, seuls quelques pourcents de la lumière solaire atteint directement la surface de Vénus). Des expressions analytiques deviennent alors délicates à trouver, mais des modèles numériques peuvent être utilisés pour déterminer les profils de température dans une colonne d'atmosphère (ce que l'on appelle un modèle 1D radiatif). On peut également profiter de la puissance de calcul des ordinateurs pour abandonner d'autres approximations : il est par exemple indispensable d'abandonner l'approximation grise en infrarouge thermique si l'on veut simuler le spectre du rayonnement thermique émis par la planète.
Gradients adiabatiques au sein des atmosphères du système solaire
| Vénus | Terre | Mars | Jupiter | Saturne | Uranus | Neptune | Titan |
|---|
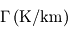 | -10.5 | -9.8 | -4.5 | -2 | -0.71 | -0.67 | -0.85 | -1.3 |
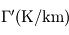 | | -5 | | | | | | -0.5 |
 Nécessité du phénomène de convection
Nécessité du phénomène de convection
La comparaison entre le profil thermique à un instant donné et le gradient adiabatique au même endroit permet de connaître la stabilité de l'atmosphère vis-à-vis des phénomènes de convection. Supposons pour bien comprendre un profil thermique isotherme. Si un mouvement local amène une parcelle de gaz à un niveau plus élevé de façon assez rapide pour qu'aucun échange thermique n'ait lieu (par conduction ou rayonnement), celle-ci va se refroidir en suivant le gradient adiabatique, et sera donc plus froide et plus dense que ses environs immédiats. Cette parcelle aura donc tendance à retomber jusqu'à son niveau de départ, puisqu'un gaz plus froid est également plus dense toutes choses égales par ailleurs : par exemple, pour un gaz parfait, 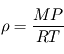 . On est donc en présence d'une atmosphère stable.
. On est donc en présence d'une atmosphère stable.
À l'inverse, si le profil thermique décroît plus fortement avec l'altitude que ce qu'indique le gradient adiabatique, cette parcelle de gaz sera certes refroidie si elle est soumise à un déplacement ascendant adiabatique, mais elle se retrouvera tout de même légèrement plus chaude que l'atmosphère environnante, et donc moins dense. Elle pourra donc continuer son mouvement ascendant jusqu'à ce qu'elle rencontre une zone stable où le profil thermique décroît moins vite que le gradient adiabatique. Une telle zone où des mouvements de convection à grande échelle peuvent se développer à partir d'une petite perturbation est dite instable. L'effet à long terme de ces mouvements de convection va conduire à un mélange qui homogénéisera le profil vertical de température jusqu'à retrouver une situation marginalement stable, c'est-à-dire avec un profil thermique suivant exactement le gradient adiabatique.
Stabilité du profil thermique
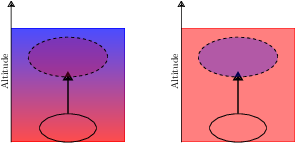
Sur l'image de gauche, le profil thermique décroît rapidement avec l'altitude (dégradé de couleur rouge vers bleu). Si une masse d'air (délimitée par l'ellipse pleine) est amenée de façon adiabatique à un niveau supérieur, son refroidissement adiabatique est insuffisant par rapport aux alentours et elle reste plus chaude que ses environs. Elle peut alors continuer à monter, le profil thermique est instable.
Sur l'image de droite, le profil thermique décroît très lentement avec l'altitude. La même masse d'air montant alors plus haut se retrouve plus froide que ses environs, et retombe alors à son niveau de départ. Le profil thermique est convectivement stable.
Crédit :
Emmanuel Marcq
Troposphère
Les profils thermiques purement radiatifs tels que ceux modélisés ici ont tendance à voir leur pente 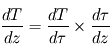 croître en valeur absolue à mesure que la profondeur optique infrarouge
croître en valeur absolue à mesure que la profondeur optique infrarouge 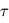 croît en s'enfonçant dans l'atmosphère profonde. Sous couvert d'hypothèses raisonnables concernant la composition du gaz considéré parfait (pour
croît en s'enfonçant dans l'atmosphère profonde. Sous couvert d'hypothèses raisonnables concernant la composition du gaz considéré parfait (pour 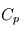 ) et la croissance de
) et la croissance de 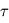 selon le niveau de pression dans l'atmosphère, il est possible (mais hors-programme) de montrer que la pente du profil radiatif excède, en valeur absolue, le gradient adiabatique pour
selon le niveau de pression dans l'atmosphère, il est possible (mais hors-programme) de montrer que la pente du profil radiatif excède, en valeur absolue, le gradient adiabatique pour 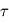 voisin de l'unité. Les régions atmosphériques situées en dessous (
voisin de l'unité. Les régions atmosphériques situées en dessous (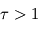 ) deviennent donc instables vis-à-vis de la convection qui s'y développe, et le profil thermique se met alors à suivre non plus la valeur donnée par le seul équilibre radiatif, mais le gradient adiabatique. On appelle cette couche atmosphérique troposphère. Les couches situées au-dessus (
) deviennent donc instables vis-à-vis de la convection qui s'y développe, et le profil thermique se met alors à suivre non plus la valeur donnée par le seul équilibre radiatif, mais le gradient adiabatique. On appelle cette couche atmosphérique troposphère. Les couches situées au-dessus (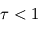 ) sont quant à elles stables vis-à-vis de la convection, et l'équilibre radiatif y est valable : on se trouve alors dans la stratosphère ou la mésosphère, selon l'existence ou non d'une inversion de température.
) sont quant à elles stables vis-à-vis de la convection, et l'équilibre radiatif y est valable : on se trouve alors dans la stratosphère ou la mésosphère, selon l'existence ou non d'une inversion de température.
Notons qu'il existe quand même une troposphère dans les atmosphères des planètes telluriques trop peu opaques au rayonnement infrarouge thermique pour avoir 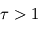 (par exemple Mars, et dans une moindre mesure la Terre). En ce cas, l'instabilité de départ est causée par la discontinuité de température au niveau de la surface planétaire (voir ici), qui donne naissance à des mouvements de convection s'étendant jusqu'à une altitude équivalente à une échelle de hauteur environ.
(par exemple Mars, et dans une moindre mesure la Terre). En ce cas, l'instabilité de départ est causée par la discontinuité de température au niveau de la surface planétaire (voir ici), qui donne naissance à des mouvements de convection s'étendant jusqu'à une altitude équivalente à une échelle de hauteur environ.
Profil thermique radiatif-convectif
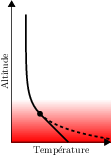
En pointillé, le profil thermique purement radiatif. En dessous d'une certaine altitude (marqué par un point noir), ce profil devient convectivement instable et la convection prend le relais pour transporter l'énergie (aidant ainsi au refroidissement de la surface). la couche atmosphérique située sous ce point s'appelle alors la troposphère, et celle au-dessus mésosphère (il n'y a pas de stratosphère dans ce profil).
Crédit :
Emmanuel Marcq
Couches atmosphériques des planètes telluriques du système solaire

Crédit :
LASP, Emmanuel Marcq (traduction)
Condition d'existence d'une stratosphère
Les profils thermiques les plus simples ne comportent qu'une troposphère surmontée d'une mésosphère, et le profil thermique y décroît toujours avec l'altitude. Mais il existe parfois au sein de la zone purement radiative une anomalie, une zone où la température croît avec l'altitude. Une telle zone est appelée stratosphère. Pour qu'une telle couche existe au sein d'une atmosphère, il faut qu'elle absorbe elle-même une partie du flux stellaire (dans le domaine visible, UV ou proche IR) et qu'elle soit relativement mauvaise émettrice en infrarouge thermique afin que l'énergie reçue par absorption du flux stellaire ne soit pas immédiatement perdue par rayonnement infrarouge thermique. Si l'on néglige les processus de diffusion lumineuse (ce qui est une hypothèse souvent vérifiée dans le domaine infrarouge thermique en l'absence de nuages, mais assez inexacte pour la lumière stellaire à plus courte longueur d'onde), le critère quantitatif pour l'existence d'une stratosphère est d'avoir une région verticale d'épaisseur optique 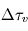 en lumière stellaire et
en lumière stellaire et 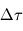 en infrarouge thermique tels que
en infrarouge thermique tels que 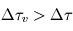 .
.
Dans le système solaire, la Terre possède une stratosphère due à la présence d'ozone, qui est un très bon absorbant de la lumière UV du Soleil. Comme, à l'altitude où cette absorption a lieu, l'atmosphère est froide et sèche, et que l'atmosphère terrestre est pauvre en 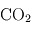 , il y a peu d'absorption du rayonnement infrarouge, et donc aussi une faible émissivité infrarouge (
, il y a peu d'absorption du rayonnement infrarouge, et donc aussi une faible émissivité infrarouge (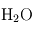 et
et 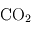 étant les gaz à effet de serre principaux au sein des atmosphères telluriques). Les conditions d'existence d'une stratosphère sont donc réunies. En revanche, les atmosphères de Vénus et de Mars, constituées principalement de
étant les gaz à effet de serre principaux au sein des atmosphères telluriques). Les conditions d'existence d'une stratosphère sont donc réunies. En revanche, les atmosphères de Vénus et de Mars, constituées principalement de 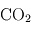 qui est un excellent émetteur infrarouge, ne possèdent pas de stratosphère. Dans le système solaire extérieur, on trouve également des stratosphères, dues à la présence de méthane (
qui est un excellent émetteur infrarouge, ne possèdent pas de stratosphère. Dans le système solaire extérieur, on trouve également des stratosphères, dues à la présence de méthane (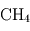 ) au sein de ces atmosphères qui absorbe bien dans l'infrarouge proche émis par le Soleil. Dans le cas de Titan, la stratosphère est due non seulement au méthane, mais aussi à l'absorption de la lumière solaire par les particules du brouillard photochimique qui l'entoure à haute altitude.
) au sein de ces atmosphères qui absorbe bien dans l'infrarouge proche émis par le Soleil. Dans le cas de Titan, la stratosphère est due non seulement au méthane, mais aussi à l'absorption de la lumière solaire par les particules du brouillard photochimique qui l'entoure à haute altitude.
Thermosphère
Thermosphère
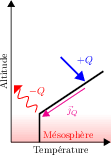
Positions respectives de la source de chaleur (
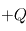
) et du puits radiatif mésosphérique (
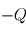
). Le profil conductif s'établit alors entre les deux avec transport par conduction de la chaleur verticalement selon
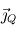
entre les deux, imposant le gradient thermique positif
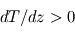
.
Crédit :
Emmanuel Marcq
Au sommet de la mésosphère, vers un niveau de pression de 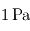 , l'atmosphère devient trop peu dense pour être efficacement absorbante au rayonnement infrarouge et ainsi échanger de l'énergie de façon radiative. Le seul phénomène encore capable de transporter l'énergie devient alors la conduction thermique, obéissant à la loi de Fourier :
, l'atmosphère devient trop peu dense pour être efficacement absorbante au rayonnement infrarouge et ainsi échanger de l'énergie de façon radiative. Le seul phénomène encore capable de transporter l'énergie devient alors la conduction thermique, obéissant à la loi de Fourier : 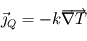 où
où 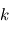 désigne la conductivité thermique du milieu et
désigne la conductivité thermique du milieu et 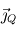 le flux de chaleur ainsi transporté. La structure thermique dans cette couche est alors dictée par la position des sources et des puits de chaleur :
le flux de chaleur ainsi transporté. La structure thermique dans cette couche est alors dictée par la position des sources et des puits de chaleur :
- la source est située à haute altitude, là où les particules énergétiques issues du vent stellaire ainsi que les photons de haute énergie (X ou
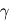 ) dissocient les molécules et/ou ionisent les atomes en leur arrachant des électrons.
) dissocient les molécules et/ou ionisent les atomes en leur arrachant des électrons. - le puits est situé à la base de la mésosphère, là où l'atmosphère redevient assez dense pour que la chaleur qui y arrive soit rayonnée efficacement vers l'espace sous forme de rayonnement infrarouge thermique
Les positions respectives de ces puits et de ces sources causent un profil thermique croissant avec l'altitude, et pouvant atteindre des températures très élevées la journée car la conductivité thermique d'un tel milieu dilué est très faible, la chaleur peut donc y être piégée de façon très efficace. On nomme donc cette couche thermosphère. Sur Terre, la dissociation des molécules de 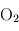 par les UV solaires est une source de chaleur intense (ces molécules très fragiles vis-à-vis des rayonnements dissociants et/ou ionisants sont nombreuses dans l'atmosphère terrestre), si bien que les températures thermosphériques peuvent atteindre des valeurs très élevées, supérieures à
par les UV solaires est une source de chaleur intense (ces molécules très fragiles vis-à-vis des rayonnements dissociants et/ou ionisants sont nombreuses dans l'atmosphère terrestre), si bien que les températures thermosphériques peuvent atteindre des valeurs très élevées, supérieures à 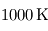 . Pour les planètes géantes du système solaire, la source d'énergie est principalement due au chauffage par effet Joule dans l'ionosphère (friction des électrons libres). En revanche, dans les atmosphères telluriques riches en
. Pour les planètes géantes du système solaire, la source d'énergie est principalement due au chauffage par effet Joule dans l'ionosphère (friction des électrons libres). En revanche, dans les atmosphères telluriques riches en 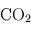 comme celles de Vénus et Mars, la dissociation des molécules est relativement difficile et le dioxyde de carbone est un radiateur efficace même à faible pression, ce qui entraîne des maxima de température diurne bien plus faible, pouvant même disparaître complètement pendant la nuit. On appelle alors parfois cette couche cryosphère lorsque ce phénomène se produit.
comme celles de Vénus et Mars, la dissociation des molécules est relativement difficile et le dioxyde de carbone est un radiateur efficace même à faible pression, ce qui entraîne des maxima de température diurne bien plus faible, pouvant même disparaître complètement pendant la nuit. On appelle alors parfois cette couche cryosphère lorsque ce phénomène se produit.
Auteur: Emmanuel Marcq
 Exercice
Exercice
Vous venez d'être embauché par un célèbre réalisateur Hollywoodien en tant que conseiller scientifique pour son prochain film de science-fiction. L'action se déroulera sur une lune tellurique nommée Pandore d'une planète géante appelée Polyphème en orbite autour de l'étoile 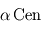 . Toutes les données numériques pertinentes se trouvent ci-dessous.
. Toutes les données numériques pertinentes se trouvent ci-dessous.
Données numériques pertinentes
Étoile (α Centauri) :
- Masse : 1,1 masse solaire
- Rayon : 1,27 rayon solaire
- Classe spectrale : G2V
- Température photosphérique : 5790 K
Polyphème :
- Masse : 0,44 masse jovienne
- Rayon : 0,75 rayon jovien
- Période de rotation : 15 h
- Période de révolution : 1,4 année terrestre
- Rayon de l'orbite : 1,32 UA
- Albédo visible : 0.4
Pandore :
- Rayon : 0,78 rayon terrestre
- Masse : 0,43 masse terrestre
- Rayon de l'orbite : 264000 km
- Période de rotation (synchrone avec révolution) : 31,5 h
- Albédo visible : 0,3
- Pression atmosphérique à la surface : 1,22 bar
- Température moyenne de surface : 27°C
- Composition atmosphérique (% en masse) :
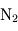 (81 %),
(81 %),  (16 %),
(16 %), 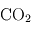 (2 %),
(2 %), 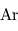 (1 %),
(1 %), 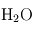 (variable),
(variable), 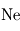 ,
, 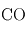 ,
, 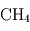 ,
, 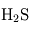 ,
, 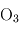 ,
, 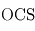 ,
, 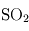 (traces).
(traces). - Capacité calorifique à pression constante : 1012 J/kg/K
Question 1)
- Quelle est la puissance lumineuse totale émise par l'étoile hôte ?
- Calculer alors la constante stellaire au niveau de l'orbite de Polyphème.
- Considérer l'étoile comme un corps noir ;
- et que la puissance émise se dilue uniformément dans l'espace jusqu'au niveau de l'orbite de Polyphème.
Question 6)
Compte tenu de la composition atmosphérique, s'attend-on à trouver une stratosphère sur Pandore ? Si oui, quelle serait l'espèce chimique responsable ?
Chercher parmi les espèces présentes celles qui absorbent les UV, et comparer leurs abondances à celle des espèces qui rayonnent bien dans l'IR thermique.
Question 8)
Calculer le gradient adiabatique sec 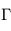 . Le gradient adiabatique humide sera-t-il inférieur ou supérieur en valeur absolue ?
. Le gradient adiabatique humide sera-t-il inférieur ou supérieur en valeur absolue ?
Applications directes des formules du cours.
Question 9)
Représenter l'allure du profil thermique moyen de Pandore. On considérera que la troposphère s'étend sur une échelle de hauteur 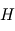 , et on fera figurer l'échelle de hauteur, les différentes couches atmosphériques et les températures à leurs limites quand cela est possible.
, et on fera figurer l'échelle de hauteur, les différentes couches atmosphériques et les températures à leurs limites quand cela est possible.
Températures importantes : au sommet de la troposphère, au sommet de l'atmosphère (voir le modèle à deux couches).
-------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------
ACCES AU PLAN DES CHAPITRES
 Prérequis
Prérequis

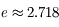 ). Le lecteur intéressé par une définition quantitative pourra se reporter
). Le lecteur intéressé par une définition quantitative pourra se reporter  pour la Terre à environ
pour la Terre à environ  pour Saturne. Ces valeurs sont en général très petites devant le rayon de la planète, si bien que l'on peut négliger la courbure de la planète et considérer l'atmosphère comme une succession de couches planes empilées de bas en haut. C'est ce que l'on appelle l'
pour Saturne. Ces valeurs sont en général très petites devant le rayon de la planète, si bien que l'on peut négliger la courbure de la planète et considérer l'atmosphère comme une succession de couches planes empilées de bas en haut. C'est ce que l'on appelle l'
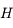 à laquelle la pression est divisée par le nombre
à laquelle la pression est divisée par le nombre 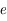 (environ 2,718). Cette altitude définit l'échelle de hauteur au niveau de la surface, proche ici de
(environ 2,718). Cette altitude définit l'échelle de hauteur au niveau de la surface, proche ici de  .
.

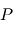 par un corps noir sur l'ensemble du spectre dans un demi-espace et par unité de surface émettrice est proportionnelle à la puissance quatrième de sa température absolue
par un corps noir sur l'ensemble du spectre dans un demi-espace et par unité de surface émettrice est proportionnelle à la puissance quatrième de sa température absolue 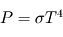 . La constante de proportionnalité
. La constante de proportionnalité 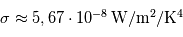 est appelée constante de Stefan-Boltzmann. Cela implique qu'un doublement de la température absolue d'un corps noir entraîne une multiplication par 16 de la puissance émise !
est appelée constante de Stefan-Boltzmann. Cela implique qu'un doublement de la température absolue d'un corps noir entraîne une multiplication par 16 de la puissance émise !
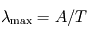 (loi de Wien). La constante
(loi de Wien). La constante 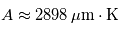 est appelée constante de Wien.
est appelée constante de Wien.
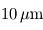 .), ou encore des étoiles dans le domaine visible.
.), ou encore des étoiles dans le domaine visible.

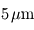 ).
).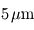 et jusqu'à quelques dizaines de micromètres (d'autant plus que la planète est froide).
et jusqu'à quelques dizaines de micromètres (d'autant plus que la planète est froide).


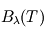 , définie comme la puissance émise par unité de surface émettrice, par angle solide autour de la direction du rayon et par unité de longueur d'onde
, définie comme la puissance émise par unité de surface émettrice, par angle solide autour de la direction du rayon et par unité de longueur d'onde 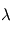 émise par tout corps noir idéal de température
émise par tout corps noir idéal de température 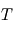 , est donnée par la loi de Planck :
, est donnée par la loi de Planck :
![\[ B_{\lambda}(T) = \frac{2 h c^2}{\lambda ^5} \frac{1}{\exp \left( \frac{hc}{\lambda kT} \right) -1} \]](../pages_fluide-temperature/equations_fluide-temperature-comprendre-noatm/equation4.png)
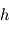 ,
, 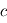 et
et 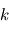 désignent respectivement les constantes fondamentales de Planck, de la vitesse de la lumière et de Maxwell-Boltzmann. Cette fonction possède des propriétés mathématiques aux conséquences importantes pour la suite du cours.
désignent respectivement les constantes fondamentales de Planck, de la vitesse de la lumière et de Maxwell-Boltzmann. Cette fonction possède des propriétés mathématiques aux conséquences importantes pour la suite du cours.
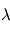 de
de 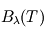 à température
à température 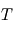 donnée, comme illustré
donnée, comme illustré 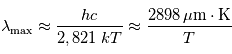
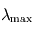 est voisin de
est voisin de 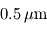 (soit dans le vert).
(soit dans le vert).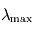 est voisin de
est voisin de 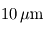 .
.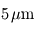 . Dans le contexte exoplanétaire, une remarque importante s'impose dès maintenant : la plupart des exoplanètes actuellement connues sont extrêmement chaudes, avec des températures excédant souvent
. Dans le contexte exoplanétaire, une remarque importante s'impose dès maintenant : la plupart des exoplanètes actuellement connues sont extrêmement chaudes, avec des températures excédant souvent 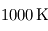 , si bien que la limite entre infrarouge thermique et lumière stellaire est décalée vers de plus courtes longueurs d'onde, voire devient complètement dénuée de sens. Cela empêche notamment d'appliquer tels quels les modèles atmosphériques conçus dans le système solaire qui distinguent ces deux catégories.
, si bien que la limite entre infrarouge thermique et lumière stellaire est décalée vers de plus courtes longueurs d'onde, voire devient complètement dénuée de sens. Cela empêche notamment d'appliquer tels quels les modèles atmosphériques conçus dans le système solaire qui distinguent ces deux catégories.
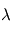 , et sur les
, et sur les 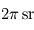 d'angle solide en question. Le calcul donne alors le résultat suivant, connu sous le nom de loi de Stefan-Boltzmann :
d'angle solide en question. Le calcul donne alors le résultat suivant, connu sous le nom de loi de Stefan-Boltzmann :
![\[ F = \sigma T^4 \]](../pages_fluide-temperature/equations_fluide-temperature-comprendre-noatm/equation20.png)
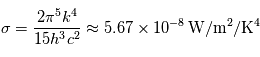 est connu sous le nom de constante de Stefan-Boltzmann. La puissance émise par un corps noir dépend donc énormément de sa température (une augmentation relative de
est connu sous le nom de constante de Stefan-Boltzmann. La puissance émise par un corps noir dépend donc énormément de sa température (une augmentation relative de 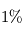 de sa température entraîne ainsi une augmentation d'environ
de sa température entraîne ainsi une augmentation d'environ 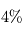 du flux émis).
du flux émis).
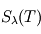 émis par un corps donné se trouvant à l'équilibre thermodynamique à la température
émis par un corps donné se trouvant à l'équilibre thermodynamique à la température 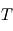 peut alors s'exprimer comme
peut alors s'exprimer comme 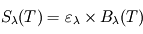 où
où 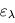 est une grandeur sans dimension appelée émissivité (qui dépend de la température, mais de façon moins marquée que la fonction de Planck
est une grandeur sans dimension appelée émissivité (qui dépend de la température, mais de façon moins marquée que la fonction de Planck 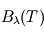 si bien que par souci d'alléger les notations, on ne la note pas en général
si bien que par souci d'alléger les notations, on ne la note pas en général 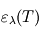 comme on le devrait en toute rigueur).
comme on le devrait en toute rigueur).
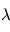 . On sait qu'une fois l'équilibre thermodynamique atteint, ces deux corps en contact radiatif auront la même température
. On sait qu'une fois l'équilibre thermodynamique atteint, ces deux corps en contact radiatif auront la même température 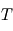 . Si l'on note
. Si l'on note 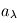 la fraction du rayonnement incident absorbée par le corps réel, que l'on appelle absorbance, il en renvoie la fraction complémentaire
la fraction du rayonnement incident absorbée par le corps réel, que l'on appelle absorbance, il en renvoie la fraction complémentaire 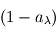 . Un bilan net des flux (nul à l'équilibre) à travers le filtre donne alors la relation
. Un bilan net des flux (nul à l'équilibre) à travers le filtre donne alors la relation 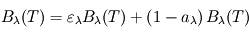 , ce qui se simplifie en
, ce qui se simplifie en 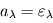 . C'est la loi de Kirchhoff, que L'on résume souvent en "les bons absorbeurs sont les bons émetteurs".
. C'est la loi de Kirchhoff, que L'on résume souvent en "les bons absorbeurs sont les bons émetteurs".
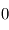 et
et  quelle que soit la longueur d'onde, l'émissivité l'est aussi. Il en résulte qu'aucun corps ne peut rayonner plus efficacement que le corps noir à longueur d'onde et température donnée.
quelle que soit la longueur d'onde, l'émissivité l'est aussi. Il en résulte qu'aucun corps ne peut rayonner plus efficacement que le corps noir à longueur d'onde et température donnée. , son absorbance est aussi égale à l'unité quelle que soit la longueur d'onde, ce qui justifie son nom de corps noir au sens où il ne réfléchit aucun rayonnement incident.
, son absorbance est aussi égale à l'unité quelle que soit la longueur d'onde, ce qui justifie son nom de corps noir au sens où il ne réfléchit aucun rayonnement incident.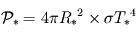
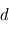 la distance de l'étoile à la planète, on obtient alors un flux (puissance par unité de surface réceptrice)
la distance de l'étoile à la planète, on obtient alors un flux (puissance par unité de surface réceptrice) 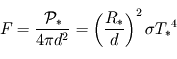
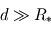 ), les rayons qu'elle émet peuvent être considérés comme parallèles. La façon la plus simple de calculer cette puissance reçue consiste donc à multiplier le flux
), les rayons qu'elle émet peuvent être considérés comme parallèles. La façon la plus simple de calculer cette puissance reçue consiste donc à multiplier le flux 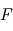 par la surface interceptant toute la lumière reçue par la planète à angle droit des rayons. Cette surface consiste donc ici en un disque du rayon
par la surface interceptant toute la lumière reçue par la planète à angle droit des rayons. Cette surface consiste donc ici en un disque du rayon 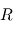 de la planète, d'où
de la planète, d'où 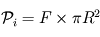
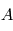 , la proportion réfléchie de la puissance incidente, la partie absorbée représente donc le complémentaire, soit
, la proportion réfléchie de la puissance incidente, la partie absorbée représente donc le complémentaire, soit 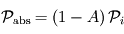 .
.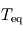 se comporte comme un corps noir aux longueurs d'ondes considérées, cette puissance rayonnée vaut alors
se comporte comme un corps noir aux longueurs d'ondes considérées, cette puissance rayonnée vaut alors 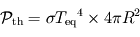 puisque l'ensemble de la planète rayonne.
puisque l'ensemble de la planète rayonne.![\[ \pi R^2 \left(1 - A \right) F = 4 \pi R^2 \sigma {T_{\mathrm{eq}}^4 \]](../pages_fluide-temperature/equations_fluide-temperature-comprendre-noatm/equation50.png)
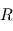 de la planète (ce qui signifie qu'en première approximation, la température d'une planète ne dépend pas de sa taille) en :
de la planète (ce qui signifie qu'en première approximation, la température d'une planète ne dépend pas de sa taille) en :
![T_{\mathrm{eq}} = \left[ \frac{\left(1 - A\right) F}{4 \sigma} \right]^{1/4} = \sqrt{\frac{R_*}{d}} \left( \frac{1-A}{4} \right)^{1/4} T_*](../pages_fluide-temperature/equations_fluide-temperature-comprendre-noatm/equation52.png)
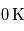 (à très grande distance) et
(à très grande distance) et 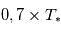 à la limite où l'orbite de la planète est tangente à son étoile (et la planète de rayon négligeable devant l'étoile).
à la limite où l'orbite de la planète est tangente à son étoile (et la planète de rayon négligeable devant l'étoile).
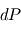 entre le haut et le bas d'une couche d'épaisseur
entre le haut et le bas d'une couche d'épaisseur 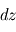 (la direction verticale étant bien définie en géométrie plan-parallèle) dépend donc de la masse contenue dans un volume de section horizontale
(la direction verticale étant bien définie en géométrie plan-parallèle) dépend donc de la masse contenue dans un volume de section horizontale 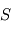 et d'épaisseur
et d'épaisseur 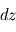 , d'où, par équilibre des forces verticales s'exerçant sur ce volume
, d'où, par équilibre des forces verticales s'exerçant sur ce volume 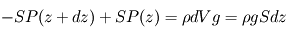
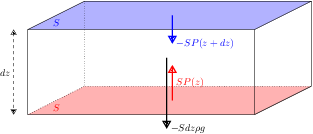
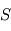 fait donc apparaître
fait donc apparaître 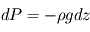 : la pression décroît bien avec l'altitude, selon la masse volumique et la gravité locales.
: la pression décroît bien avec l'altitude, selon la masse volumique et la gravité locales.
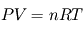 , où
, où 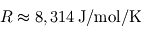 désigne la constante des gaz parfaits, P la pression, V le volume occupé, n le nombre de moles et T la température n'est pas vraiment adaptée à une formulation locale (intensive, dirait-on en thermodynamique). Il vaut mieux la présenter sous la forme
désigne la constante des gaz parfaits, P la pression, V le volume occupé, n le nombre de moles et T la température n'est pas vraiment adaptée à une formulation locale (intensive, dirait-on en thermodynamique). Il vaut mieux la présenter sous la forme 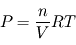 , où l'on voit apparaître la densité molaire (homogène à des
, où l'on voit apparaître la densité molaire (homogène à des 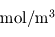 ) locale. Or, cette grandeur est proportionnelle à la masse volumique selon la relation
) locale. Or, cette grandeur est proportionnelle à la masse volumique selon la relation 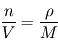 où
où 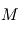 désigne la masse molaire. Il est alors possible d'exprimer la masse volumique du gaz parfait en fonction des conditions de pression et température locales, ainsi que de la masse molaire du gaz constituant :
désigne la masse molaire. Il est alors possible d'exprimer la masse volumique du gaz parfait en fonction des conditions de pression et température locales, ainsi que de la masse molaire du gaz constituant : 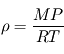 .
.
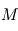 , et que l'atmosphère est de surcroît isotherme à la température
, et que l'atmosphère est de surcroît isotherme à la température 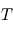 selon l'altitude. L'utilisation de l'équation d'état du gaz parfait au sein de l'équilibre hydrostatique donne, par substitution de
selon l'altitude. L'utilisation de l'équation d'état du gaz parfait au sein de l'équilibre hydrostatique donne, par substitution de 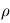 ,
, 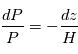 avec
avec 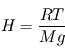 désignant une grandeur homogène à une altitude. On l'appelle échelle de hauteur, et son interprétation est plus claire en intégrant l'équation différentielle où elle apparaît, avec la condition à la limite inférieure
désignant une grandeur homogène à une altitude. On l'appelle échelle de hauteur, et son interprétation est plus claire en intégrant l'équation différentielle où elle apparaît, avec la condition à la limite inférieure 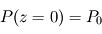 :
:
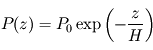
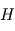 représente donc la hauteur caractéristique avec laquelle la pression décroît avec l'altitude pour tendre vers
représente donc la hauteur caractéristique avec laquelle la pression décroît avec l'altitude pour tendre vers 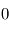 dans l'espace interplanétaire à grande distance de la planète (mais l'approximation plan-parallèle, ainsi que la thermodynamique usuelle à l'équilibre cessent d'être valides à quelques dizaines d'échelles de hauteur au-dessus de la surface).
dans l'espace interplanétaire à grande distance de la planète (mais l'approximation plan-parallèle, ainsi que la thermodynamique usuelle à l'équilibre cessent d'être valides à quelques dizaines d'échelles de hauteur au-dessus de la surface).
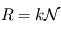 où
où 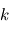 désigne la constante de Maxwell-Boltzmann et
désigne la constante de Maxwell-Boltzmann et 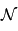 la constante d'Avogadro, puis simplifier dans l'expression de
la constante d'Avogadro, puis simplifier dans l'expression de 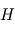 . On obtient alors
. On obtient alors 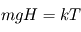 où
où 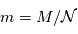 désigne la masse d'une molécule de gaz : une molécule de gaz à la hauteur caractéristique possède donc une énergie potentielle de pesanteur du même ordre que son énergie cinétique microscopique (thermique) moyenne. On comprend donc bien pourquoi
désigne la masse d'une molécule de gaz : une molécule de gaz à la hauteur caractéristique possède donc une énergie potentielle de pesanteur du même ordre que son énergie cinétique microscopique (thermique) moyenne. On comprend donc bien pourquoi 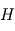 représente le compromis entre l'agitation thermique qui tend à disperser les atmosphères (
représente le compromis entre l'agitation thermique qui tend à disperser les atmosphères (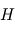 est croissant avec
est croissant avec 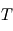 ), et le poids qui a tendance à tasser les atmosphères vers le bas :
), et le poids qui a tendance à tasser les atmosphères vers le bas : 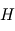 décroît avec
décroît avec 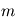 (atmosphère dense) et
(atmosphère dense) et 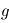 (gravité forte).
(gravité forte).
 en infrarouge thermique, et que celle de l'atmosphère (directement reliée à son absorbance via la
en infrarouge thermique, et que celle de l'atmosphère (directement reliée à son absorbance via la 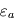 dans tout le domaine infrarouge thermique (c'est ce que l'on appelle l'approximation grise). L'atmosphère est considérée ici isotherme à la température
dans tout le domaine infrarouge thermique (c'est ce que l'on appelle l'approximation grise). L'atmosphère est considérée ici isotherme à la température 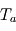 . On négligera aussi les flux d'énergie éventuels provenant de l'intérieur de la planète, et on supposera que l'étoile émet de façon négligeable dans l'infrarouge thermique, situé loin de son maximum d'émission dans le visible (ou le proche IR pour les plus froides d'entre elles).
. On négligera aussi les flux d'énergie éventuels provenant de l'intérieur de la planète, et on supposera que l'étoile émet de façon négligeable dans l'infrarouge thermique, situé loin de son maximum d'émission dans le visible (ou le proche IR pour les plus froides d'entre elles).

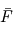 désigne le flux moyen à la surface de la planète, qui se déduit du flux à incidence normale appelé constante solaire (ou stellaire) par l'égalité des puissances :
désigne le flux moyen à la surface de la planète, qui se déduit du flux à incidence normale appelé constante solaire (ou stellaire) par l'égalité des puissances : 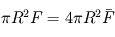 (voir le raisonnement définissant la
(voir le raisonnement définissant la 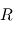 désigne ici le rayon planétaire). On en déduit immédiatement
désigne ici le rayon planétaire). On en déduit immédiatement 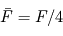 : un facteur 2 s'explique aisément par le fait que seul un hémisphère est éclairé, et l'autre facteur 2 par la moyenne du cosinus de l'angle d'incidence intervenant dans le calcul local du flux.
: un facteur 2 s'explique aisément par le fait que seul un hémisphère est éclairé, et l'autre facteur 2 par la moyenne du cosinus de l'angle d'incidence intervenant dans le calcul local du flux.
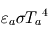 dans chacun des demi-espaces inférieur (vers la surface) et supérieur (vers l'espace). En vertu de la loi de Kirchhoff, cette émissivité est égale à son absorbance, si bien que la fraction complémentaire
dans chacun des demi-espaces inférieur (vers la surface) et supérieur (vers l'espace). En vertu de la loi de Kirchhoff, cette émissivité est égale à son absorbance, si bien que la fraction complémentaire 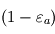 du rayonnement en provenance de la surface (considérée comme un corps noir) réussit à la traverser, le reste étant absorbé (on néglige les processus de diffusion ici ; seules les émissions et absorptions sont prises en compte).
du rayonnement en provenance de la surface (considérée comme un corps noir) réussit à la traverser, le reste étant absorbé (on néglige les processus de diffusion ici ; seules les émissions et absorptions sont prises en compte).
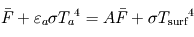 , tandis que celui au niveau de la couche atmosphérique donne
, tandis que celui au niveau de la couche atmosphérique donne 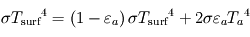 . Nous avons donc deux équations pour les deux inconnues
. Nous avons donc deux équations pour les deux inconnues 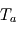 et
et 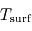 , et la résolution du système donne alors :
, et la résolution du système donne alors : 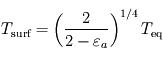 et
et 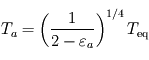 où l'on aura reconnu la température d'équilibre
où l'on aura reconnu la température d'équilibre ![T_{\mathrm{eq}} = \left[\frac{(1-A) F}{4 \sigma} \right]^{1/4} = \left[\frac{(1-A) \bar{F}}{\sigma} \right]^{1/4}](../pages_fluide-temperature/equations_fluide-temperature-comprendre-structure/equation51.png) définie précédemment.
définie précédemment.
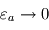 ,
, 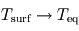 et
et 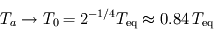 : la surface retrouve alors la température d'équilibre, ce qui est normal pour une atmosphère à la fois transparente en lumière stellaire et en infrarouge thermique (atmosphère radiativement inerte ne causant aucun effet de serre). La température atmosphérique tend alors vers une valeur
: la surface retrouve alors la température d'équilibre, ce qui est normal pour une atmosphère à la fois transparente en lumière stellaire et en infrarouge thermique (atmosphère radiativement inerte ne causant aucun effet de serre). La température atmosphérique tend alors vers une valeur 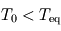 appelée température de peau et typique des couches quasi-transparentes en approximation grise.
appelée température de peau et typique des couches quasi-transparentes en approximation grise.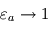 ,
, 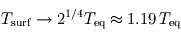 et
et 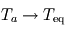 : le rayonnement s'échappant vers l'espace provient alors uniquement de l'atmosphère, qui se met donc à la température d'équilibre. La surface reçoit donc du rayonnement infrarouge atmosphérique en plus du seul rayonnement stellaire (qui pris isolément la maintiendrait déjà à une température de
: le rayonnement s'échappant vers l'espace provient alors uniquement de l'atmosphère, qui se met donc à la température d'équilibre. La surface reçoit donc du rayonnement infrarouge atmosphérique en plus du seul rayonnement stellaire (qui pris isolément la maintiendrait déjà à une température de 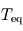 ), si bien que sa température s'élève : c'est ce que l'on appelle l'effet de serre, plafonnant dans ce modèle à une seule couche atmosphérique isotherme à une augmentation de la température absolue (mesurée en Kelvins) de
), si bien que sa température s'élève : c'est ce que l'on appelle l'effet de serre, plafonnant dans ce modèle à une seule couche atmosphérique isotherme à une augmentation de la température absolue (mesurée en Kelvins) de 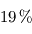 .
. 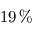 . Ceci est insuffisant dans le cas des atmosphères très épaisses comme celle de Vénus, où le rapport
. Ceci est insuffisant dans le cas des atmosphères très épaisses comme celle de Vénus, où le rapport 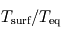 excède
excède 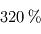 ! Cela signifie que de telles atmosphères ne peuvent se modéliser par une unique couche isotherme, même totalement absorbante aux rayons infrarouges. Il existe différents modèles plus complexes permettant de mieux rendre compte des effets de serre intenses.
! Cela signifie que de telles atmosphères ne peuvent se modéliser par une unique couche isotherme, même totalement absorbante aux rayons infrarouges. Il existe différents modèles plus complexes permettant de mieux rendre compte des effets de serre intenses.
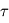 en infrarouge thermique :
en infrarouge thermique : 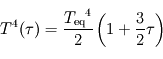 . Notons que dans ce modèle, on obtient
. Notons que dans ce modèle, on obtient 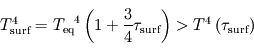 : le seul équilibre radiatif tend à créer une discontinuité de température au niveau de la surface, ce qui déclencherait alors des processus de convection pour y remédier. Un tel contraste thermique est néanmoins observable à la surface des planètes telluriques éclairées par le Soleil, comme une plage sur Terre par beau temps (le sable peut alors être brûlant et l'air frais), ou mieux encore dans les déserts de Mars.
: le seul équilibre radiatif tend à créer une discontinuité de température au niveau de la surface, ce qui déclencherait alors des processus de convection pour y remédier. Un tel contraste thermique est néanmoins observable à la surface des planètes telluriques éclairées par le Soleil, comme une plage sur Terre par beau temps (le sable peut alors être brûlant et l'air frais), ou mieux encore dans les déserts de Mars.
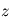 et
et 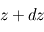 d'une masse
d'une masse 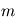 d'un gaz de capacité calorifique à pression constante Cp, d'entropie S et de volume V à la pression P et à la température T, un bilan de son enthalpie H donne
d'un gaz de capacité calorifique à pression constante Cp, d'entropie S et de volume V à la pression P et à la température T, un bilan de son enthalpie H donne 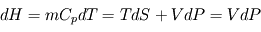 puisque
puisque 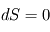 (déplacement adiabatique). La variation de pression
(déplacement adiabatique). La variation de pression 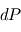 étant reliée au déplacement vertical selon la
étant reliée au déplacement vertical selon la 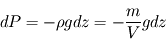 , on obtient alors
, on obtient alors 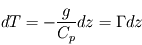 en posant
en posant 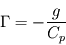 , appelé gradient adiabatique (sec). La détente adiabatique d'une parcelle de gaz ascendante conduit donc à un refroidissement proportionnel à la différence d'altitude selon le gradient adiabatique.
, appelé gradient adiabatique (sec). La détente adiabatique d'une parcelle de gaz ascendante conduit donc à un refroidissement proportionnel à la différence d'altitude selon le gradient adiabatique.
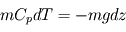 : la variation d'enthalpie du gaz (son "énergie thermique" en tenant compte des forces de pression) est directement reliée à sa variation d'énergie potentielle. Faire monter une parcelle de gaz lui coûte de l'énergie potentielle, ce qui est prélevé sur l'énergie thermique interne de ce gaz en l'absence de chaleur communiquée depuis l'extérieur.
: la variation d'enthalpie du gaz (son "énergie thermique" en tenant compte des forces de pression) est directement reliée à sa variation d'énergie potentielle. Faire monter une parcelle de gaz lui coûte de l'énergie potentielle, ce qui est prélevé sur l'énergie thermique interne de ce gaz en l'absence de chaleur communiquée depuis l'extérieur.
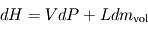 où
où 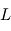 désigne l'enthalpie massique de condensation et
désigne l'enthalpie massique de condensation et 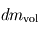 la masse d'espèce volatile qui se condense au cours du déplacement au sein de la parcelle de gaz. On arrive alors à l'expression suivante pour le nouveau gradient adiabatique
la masse d'espèce volatile qui se condense au cours du déplacement au sein de la parcelle de gaz. On arrive alors à l'expression suivante pour le nouveau gradient adiabatique 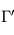 (dit gradient adiabatique humide) :
(dit gradient adiabatique humide) : 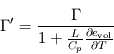 où
où 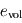 désigne la fraction massique du volatil au sein de la parcelle de gaz. On constate alors que
désigne la fraction massique du volatil au sein de la parcelle de gaz. On constate alors que 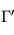 est plus faible que
est plus faible que 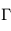 en valeur absolue : la libération de chaleur latente par liquéfaction ou condensation compense partiellement le refroidissement dû à l'ascension.
en valeur absolue : la libération de chaleur latente par liquéfaction ou condensation compense partiellement le refroidissement dû à l'ascension.
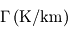
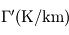
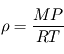 . On est donc en présence d'une atmosphère stable.
. On est donc en présence d'une atmosphère stable.

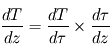 croître en valeur absolue à mesure que la profondeur optique infrarouge
croître en valeur absolue à mesure que la profondeur optique infrarouge 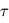 croît en s'enfonçant dans l'atmosphère profonde. Sous couvert d'hypothèses raisonnables concernant la composition du gaz considéré parfait (pour
croît en s'enfonçant dans l'atmosphère profonde. Sous couvert d'hypothèses raisonnables concernant la composition du gaz considéré parfait (pour 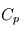 ) et la croissance de
) et la croissance de 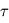 selon le niveau de pression dans l'atmosphère, il est possible (mais hors-programme) de montrer que la pente du profil radiatif excède, en valeur absolue, le gradient adiabatique pour
selon le niveau de pression dans l'atmosphère, il est possible (mais hors-programme) de montrer que la pente du profil radiatif excède, en valeur absolue, le gradient adiabatique pour 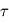 voisin de l'unité. Les régions atmosphériques situées en dessous (
voisin de l'unité. Les régions atmosphériques situées en dessous (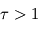 ) deviennent donc instables vis-à-vis de la convection qui s'y développe, et le profil thermique se met alors à suivre non plus la valeur donnée par le seul équilibre radiatif, mais le gradient adiabatique. On appelle cette couche atmosphérique troposphère. Les couches situées au-dessus (
) deviennent donc instables vis-à-vis de la convection qui s'y développe, et le profil thermique se met alors à suivre non plus la valeur donnée par le seul équilibre radiatif, mais le gradient adiabatique. On appelle cette couche atmosphérique troposphère. Les couches situées au-dessus (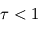 ) sont quant à elles stables vis-à-vis de la convection, et l'équilibre radiatif y est valable : on se trouve alors dans la stratosphère ou la mésosphère, selon l'existence ou non d'une inversion de température.
) sont quant à elles stables vis-à-vis de la convection, et l'équilibre radiatif y est valable : on se trouve alors dans la stratosphère ou la mésosphère, selon l'existence ou non d'une inversion de température.
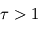 (par exemple Mars, et dans une moindre mesure la Terre). En ce cas, l'instabilité de départ est causée par la discontinuité de température au niveau de la surface planétaire (voir
(par exemple Mars, et dans une moindre mesure la Terre). En ce cas, l'instabilité de départ est causée par la discontinuité de température au niveau de la surface planétaire (voir 
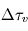 en lumière stellaire et
en lumière stellaire et 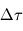 en infrarouge thermique tels que
en infrarouge thermique tels que 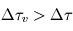 .
.
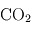 , il y a peu d'absorption du rayonnement infrarouge, et donc aussi une faible émissivité infrarouge (
, il y a peu d'absorption du rayonnement infrarouge, et donc aussi une faible émissivité infrarouge (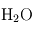 et
et 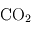 étant les gaz à effet de serre principaux au sein des atmosphères telluriques). Les conditions d'existence d'une stratosphère sont donc réunies. En revanche, les atmosphères de Vénus et de Mars, constituées principalement de
étant les gaz à effet de serre principaux au sein des atmosphères telluriques). Les conditions d'existence d'une stratosphère sont donc réunies. En revanche, les atmosphères de Vénus et de Mars, constituées principalement de 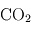 qui est un excellent émetteur infrarouge, ne possèdent pas de stratosphère. Dans le système solaire extérieur, on trouve également des stratosphères, dues à la présence de méthane (
qui est un excellent émetteur infrarouge, ne possèdent pas de stratosphère. Dans le système solaire extérieur, on trouve également des stratosphères, dues à la présence de méthane (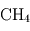 ) au sein de ces atmosphères qui absorbe bien dans l'infrarouge proche émis par le Soleil. Dans le cas de Titan, la stratosphère est due non seulement au méthane, mais aussi à l'absorption de la lumière solaire par les particules du brouillard photochimique qui l'entoure à haute altitude.
) au sein de ces atmosphères qui absorbe bien dans l'infrarouge proche émis par le Soleil. Dans le cas de Titan, la stratosphère est due non seulement au méthane, mais aussi à l'absorption de la lumière solaire par les particules du brouillard photochimique qui l'entoure à haute altitude.

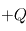 ) et du puits radiatif mésosphérique (
) et du puits radiatif mésosphérique (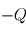 ). Le profil conductif s'établit alors entre les deux avec transport par conduction de la chaleur verticalement selon
). Le profil conductif s'établit alors entre les deux avec transport par conduction de la chaleur verticalement selon 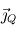 entre les deux, imposant le gradient thermique positif
entre les deux, imposant le gradient thermique positif 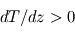 .
.
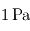 , l'atmosphère devient trop peu dense pour être efficacement absorbante au rayonnement infrarouge et ainsi échanger de l'énergie de façon radiative. Le seul phénomène encore capable de transporter l'énergie devient alors la conduction thermique, obéissant à la loi de Fourier :
, l'atmosphère devient trop peu dense pour être efficacement absorbante au rayonnement infrarouge et ainsi échanger de l'énergie de façon radiative. Le seul phénomène encore capable de transporter l'énergie devient alors la conduction thermique, obéissant à la loi de Fourier : 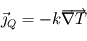 où
où 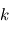 désigne la conductivité thermique du milieu et
désigne la conductivité thermique du milieu et 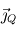 le flux de chaleur ainsi transporté. La structure thermique dans cette couche est alors dictée par la position des sources et des puits de chaleur :
le flux de chaleur ainsi transporté. La structure thermique dans cette couche est alors dictée par la position des sources et des puits de chaleur :
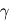 ) dissocient les molécules et/ou ionisent les atomes en leur arrachant des électrons.
) dissocient les molécules et/ou ionisent les atomes en leur arrachant des électrons.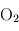 par les UV solaires est une source de chaleur intense (ces molécules très fragiles vis-à-vis des rayonnements dissociants et/ou ionisants sont nombreuses dans l'atmosphère terrestre), si bien que les températures thermosphériques peuvent atteindre des valeurs très élevées, supérieures à
par les UV solaires est une source de chaleur intense (ces molécules très fragiles vis-à-vis des rayonnements dissociants et/ou ionisants sont nombreuses dans l'atmosphère terrestre), si bien que les températures thermosphériques peuvent atteindre des valeurs très élevées, supérieures à 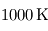 . Pour les planètes géantes du système solaire, la source d'énergie est principalement due au chauffage par effet Joule dans l'ionosphère (friction des électrons libres). En revanche, dans les atmosphères telluriques riches en
. Pour les planètes géantes du système solaire, la source d'énergie est principalement due au chauffage par effet Joule dans l'ionosphère (friction des électrons libres). En revanche, dans les atmosphères telluriques riches en 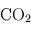 comme celles de Vénus et Mars, la dissociation des molécules est relativement difficile et le dioxyde de carbone est un radiateur efficace même à faible pression, ce qui entraîne des maxima de température diurne bien plus faible, pouvant même disparaître complètement pendant la nuit. On appelle alors parfois cette couche cryosphère lorsque ce phénomène se produit.
comme celles de Vénus et Mars, la dissociation des molécules est relativement difficile et le dioxyde de carbone est un radiateur efficace même à faible pression, ce qui entraîne des maxima de température diurne bien plus faible, pouvant même disparaître complètement pendant la nuit. On appelle alors parfois cette couche cryosphère lorsque ce phénomène se produit.

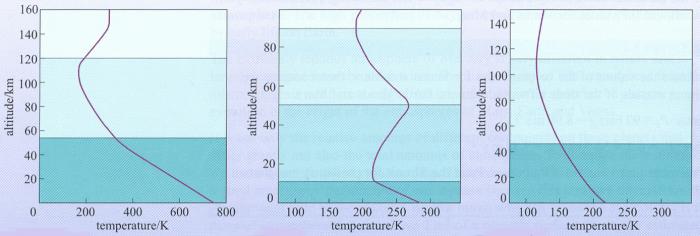
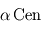 . Toutes les données numériques pertinentes se trouvent ci-dessous.
. Toutes les données numériques pertinentes se trouvent ci-dessous.
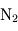 (81 %),
(81 %),  (16 %),
(16 %), 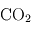 (2 %),
(2 %), 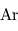 (1 %),
(1 %), 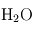 (variable),
(variable), 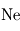 ,
, 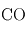 ,
, 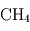 ,
, 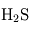 ,
, 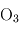 ,
, 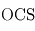 ,
, 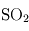 (traces).
(traces).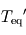 de la planète géante
de la planète géante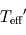 de Polyphème sera-t-elle supérieure ou inférieure à
de Polyphème sera-t-elle supérieure ou inférieure à 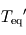 ? Justifier.
? Justifier.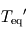 .
.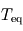 de Pandore. La comparer à celle du point triple de l'eau, égale à
de Pandore. La comparer à celle du point triple de l'eau, égale à 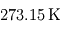 . Que vaut alors
. Que vaut alors 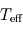 ?
?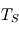 et
et 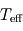 ? En donner une explication qualitative.
? En donner une explication qualitative.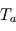 .
.
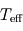 .
.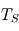 et
et 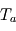 en fonction de
en fonction de 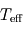 .
.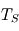 donnée dans l'énoncé. Que constate-t-on ? Proposer une explication.
donnée dans l'énoncé. Que constate-t-on ? Proposer une explication.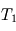 et celle de la couche profonde
et celle de la couche profonde 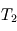 . La couche 1 absorbe une fraction
. La couche 1 absorbe une fraction 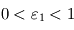 du rayonnement IR thermique. Ces deux couches sont toujours considérées parfaitement transparentes en lumière visible.
du rayonnement IR thermique. Ces deux couches sont toujours considérées parfaitement transparentes en lumière visible.
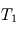 ,
, 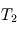 et
et 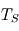 . On fera apparaître l'expression de
. On fera apparaître l'expression de 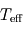 dans ce système.
dans ce système.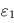 , puis celles de
, puis celles de 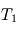 et
et 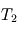 .
.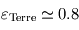 ). Comparer l'intensité de l'effet de serre sur Terre et sur Pandore.
). Comparer l'intensité de l'effet de serre sur Terre et sur Pandore.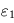 en fonction de
en fonction de 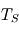 que l'énoncé donne, puis on injectera la valeur de
que l'énoncé donne, puis on injectera la valeur de 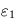 dans les expressions de
dans les expressions de 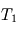 et
et 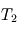 .
. 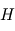 au niveau de la surface.
au niveau de la surface.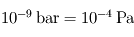 . Estimer l'altitude de cette exobase (on considérera
. Estimer l'altitude de cette exobase (on considérera 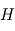 constant pour ce calcul).
constant pour ce calcul).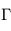 . Le gradient adiabatique humide sera-t-il inférieur ou supérieur en valeur absolue ?
. Le gradient adiabatique humide sera-t-il inférieur ou supérieur en valeur absolue ?
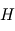 , et on fera figurer l'échelle de hauteur, les différentes couches atmosphériques et les températures à leurs limites quand cela est possible.
, et on fera figurer l'échelle de hauteur, les différentes couches atmosphériques et les températures à leurs limites quand cela est possible.
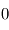 et
et 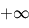 .
.
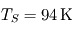 ). Pour quelle opacité de la couche n°1 ce résultat est-il obtenu ?
). Pour quelle opacité de la couche n°1 ce résultat est-il obtenu ?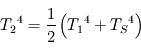
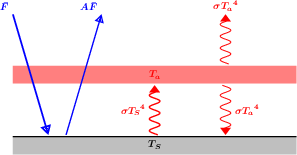
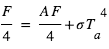 , d'où
, d'où 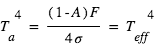 et donc
et donc 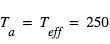 K
K 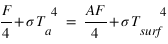
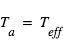 on déduit du bilan donné en 3 que
on déduit du bilan donné en 3 que 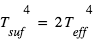 d'où
d'où 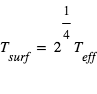
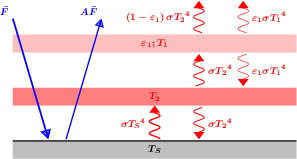
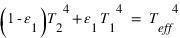 ,
, 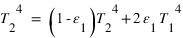 et
et 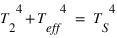
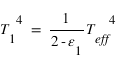 ,
, 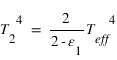 et
et 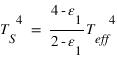 . D'où
. D'où 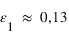 ,
,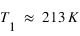 et
et 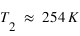 .
. 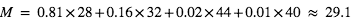 g/mol .
g/mol . 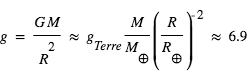 m/s2
m/s2 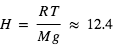 km
km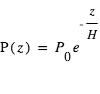 en supposant l'échelle de hauteur constante, d'où
en supposant l'échelle de hauteur constante, d'où 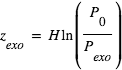 avec
avec 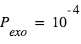 Pa,
Pa, 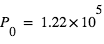 Pa et H = 12.4 km. On trouve H ≈ 260 km
Pa et H = 12.4 km. On trouve H ≈ 260 km