Atmosphère isotherme

Auteur: EM

Équation hydrostatique en géométrie plan-parallèle

Cette équation relie l'augmentation de la pression en descendant avec la masse volumique locale (autrement dit, elle exprime le fait que l'origine physique de la pression au sein des atmosphères est le poids de la colonne de gaz située à la verticale). La différence de pression 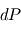entre le haut et le bas d'une couche d'épaisseur 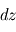(la direction verticale étant bien définie en géométrie plan-parallèle) dépend donc de la masse contenue dans un volume de section horizontale 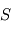et d'épaisseur 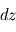, d'où, par équilibre des forces verticales s'exerçant sur ce volume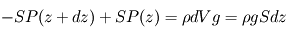 $-S P(z+dz) + S P(z) = \rho dV g = \rho g S dz$

Équilibre hydrostatique

Schéma des forces appliquées à une tranche d'air à l'équilibre.

Crédit : Emmanuel Marcq

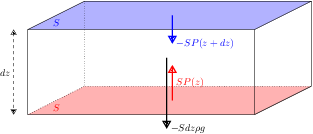
Une simplification par 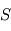fait donc apparaître 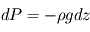$dP = - \rho g dz$ : la pression décroît bien avec l'altitude, selon la masse volumique et la gravité locales.

Reformulation de l'équation d'état du gaz parfait

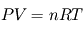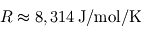La forme habituelle de cette équation PV = nRT , où $R \approx 8,314\,\mathrm{J/mol/K}$ désigne la constante des gaz parfaits, P la pression, V le volume occupé, n le nombre de moles et T la température n'est pas vraiment adaptée à une formulation locale (intensive, dirait-on en thermodynamique). Il vaut mieux la présenter sous la forme 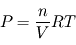$P = \frac{n}{V} RT$ , où l'on voit apparaître la densité molaire (homogène à des 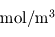$\mathrm{mol/m^3}$ ) locale. Or, cette grandeur est proportionnelle à la masse volumique selon la relation 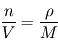$\frac{n}{V} = \frac{\rho}{M}$ où 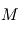désigne la masse molaire. 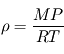Il est alors possible d'exprimer la masse volumique du gaz parfait en fonction des conditions de pression et température locales, ainsi que de la masse molaire du gaz constituant : $\rho = \frac{MP}{RT}$ .

Échelle de hauteur

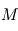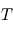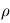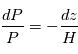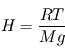On suppose ici que l'atmosphère est constituée d'un gaz parfait de masse molaire , et que l'atmosphère est de surcroît isotherme à la température selon l'altitude. L'utilisation de l'équation d'état du gaz parfait au sein de l'équilibre hydrostatique donne, par substitution de $\rho$ , $\frac{dP}{P} = - \frac{dz}{H}$ avec $H = \frac{RT}{Mg}$ désignant une grandeur homogène à une altitude. 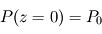On l'appelle échelle de hauteur, et son interprétation est plus claire en intégrant l'équation différentielle où elle apparaît, avec la condition à la limite inférieure P(z=0) = P_0 :

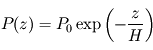
$\[ P(z) = P_0 \exp \left( - \frac{z}{H} \right)$

L'échelle de hauteur 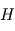représente donc la hauteur caractéristique avec laquelle la pression décroît avec l'altitude pour tendre vers 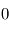dans l'espace interplanétaire à grande distance de la planète (mais l'approximation plan-parallèle, ainsi que la thermodynamique usuelle à l'équilibre cessent d'être valides à quelques dizaines d'échelles de hauteur au-dessus de la surface).

Dans le cas d'une atmosphère non isotherme, la résolution formelle est un peu plus complexe, mais l'idée générale d'une décroissance localement exponentielle selon une échelle de hauteur locale dépendant de la température locale reste valable.

Autre interprétation de l'échelle de hauteur

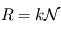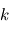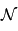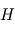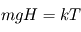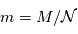On peut reformuler la constante des gaz parfaits selon $R = k \mathcal{N}$ où désigne la constante de Maxwell-Boltzmann et $\mathcal{N}$ la constante d'Avogadro, puis simplifier dans l'expression de . On obtient alors mgH = kT où $m = M/\mathcal{N}$ désigne la masse d'une molécule de gaz : une molécule de gaz à la hauteur caractéristique possède donc une énergie potentielle de pesanteur du même ordre que son énergie cinétique microscopique (thermique) moyenne. On comprend donc bien pourquoi 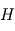représente le compromis entre l'agitation thermique qui tend à disperser les atmosphères ( 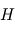est croissant avec 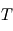), et le poids qui a tendance à tasser les atmosphères vers le bas : 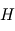décroît avec 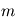(atmosphère dense) et 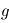(gravité forte).