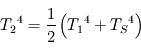mise à jour : 1 février 2022
mise à jour : 1 février 2022
 Énoncé Énoncé
|
Auteur: EM
 Introduction
Introduction
Hypothèses du modèle
Le but de ce mini-projet est de gagner une compréhension plus intuitive de l'équilibre radiatif au sein d'une atmosphère tellurique, et notamment du phénomène d'effet de serre, au moyen d'un modèle simplifié basé sur des hypothèses simplificatrices vues dans ce cours. Ceci permettra de vérifier par le calcul les résultats obtenus en manipulant ce modèle.
Le modèle est donc plan-parallèle, et traite le spectre électromagnétique en deux domaines distincts : le visible/UV/IR proche (shortwave, SW) et l'infrarouge thermique (longwave, LW ou IR). Ces deux domaines sont traités chacun de façon grise. L'atmosphère est constituée de deux couches considérées isothermes, pouvant absorber et émettre tout ou partie des rayonnements IR thermiques. Le rayonnement SW n'est quant à lui absorbé que par la surface, l'atmosphère étant donc parfaitement transparente. Les échanges autres que radiatifs sont négligés par ce modèle.
Réglages
Voici la signification des différents champs à remplir :
- Flux solaire moyen : il s'agit du flux stellaire moyenné dans le temps et dans l'espace au sommet de l'atmosphère. À ne pas confondre avec la constante stellaire, qui n'est pas moyennée !
- Albédo bolométrique : c'est la fraction (en puissance) du flux SW renvoyé vers l'espace par la surface de la planète.
- Opacités des couches 1 et 2 : il s'agit des épaisseurs optiques en IR thermique, variant donc entre
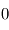 et
et 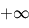 .
.
Calculatrice

Questions
Atmosphère transparente en IR
- Comment régler les opacités des couches atmosphériques pour obtenir une atmosphère transparente en infrarouge thermique ?
- En cherchant l'albédo bolométrique de la Terre et le flux solaire moyen sur Internet, remplissez les champs appropriés. Que remarque-t-on pour les températures ?
- Justifiez le résultat obtenu pour la température de surface. À quelle valeur remarquable est-elle égale ? Vérifiez que cette égalité est maintenue en changeant la valeur de certains paramètres que l'on précisera.
- Bonus : essayez de reproduire la température diurne au point subsolaire dans le cas de la Lune et de Mercure.
Effet de serre à une couche
- Essayez diverses valeurs de l'opacité IR pour la couche la plus proche de la surface (couche n°2). Que remarque-t-on à propos des températures ? Comment s'appelle ce phénomène ?
- Que se passe-t-il dans le cas où l'on fait tendre l'opacité IR de cette couche vers l'infini ? Effectuez alors par vous-même le calcul théorique et justifiez les valeurs obtenues par le modèle.
- En déduire la fourchette de valeurs pour la température de surface dans ce cas de figure en fonction de la température d'équilibre correspondante.
- Essayez de reproduire avec ce modèle les températures de surface des corp suivants (à rechercher sur Internet) : Terre, Mars, Vénus, Titan.
- Que remarque-t-on pour ces deux derniers cas ? Proposez une amélioration du modèle.
Effet de serre à deux couches
Dans cette partie, on fixe l'opacité de la couche n°2 à proximité de la surface à une valeur très élevée, et on ajuste seulement l'opacité de la couche n°1.
- Que remarque-t-on concernant les températures ?
- Déterminer la nouvelle fourchette possible pour la température de surface. Justifier les températures obtenues quand les couches n°1 et n°2 sont toutes deux complètement opaques au rayonnement IR.
- Essayez à présent de reproduire la température que l'on aurait sur Titan en l'absence de nuages (
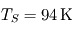 ). Pour quelle opacité de la couche n°1 ce résultat est-il obtenu ?
). Pour quelle opacité de la couche n°1 ce résultat est-il obtenu ? - Que remarque-t-on pour le cas de Vénus ? Comment améliorer encore ce modèle ?
Pour aller plus loin
- On fixe à présent l'opacité de la couche n°2 à une valeur très faible, et celle de la couche n°1 à une valeur très élevée.
- Montrer que
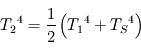
- Vérifiez que le modèle donne le même résultat.
- Peut-on reproduire une stratosphère avec ce modèle ? Pourquoi ? Que faudrait-il ajouter comme paramètre réglable pour pouvoir le faire ?
- Comment prendre en compte l'effet radiatif en lumière SW des nuages avec ce modèle simplifié ? Comment pourrait-on améliorer leur prise en compte dans ce modèle ?
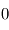 et
et 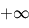 .
.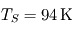 ). Pour quelle opacité de la couche n°1 ce résultat est-il obtenu ?
). Pour quelle opacité de la couche n°1 ce résultat est-il obtenu ?