Loi de Kirchhoff

Auteur: EM

Émissivité

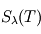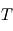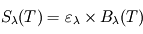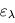Le corps noir est un modèle abstrait que l'on ne rencontre pas dans la vie courante. Le spectre thermique $S_{\lambda}(T)$ émis par un corps donné se trouvant à l'équilibre thermodynamique à la température peut alors s'exprimer comme $S_{\lambda}(T) = \varepsilon_{\lambda}\times B_{\lambda}(T)$ où $\varepsilon_{\lambda}$ est une grandeur sans dimension appelée émissivité (qui dépend de la température, mais de façon moins marquée que la fonction de Planck 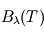$B_{\lambda}(T)$ si bien que par souci d'alléger les notations, on ne la note pas en général 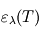$\varepsilon_{\lambda}(T)$ comme on le devrait en toute rigueur).

Loi de Kirchhoff

Considérons un corps noir en contact radiatif avec un corps réel à travers un filtre laissant seulement passer les radiations à la longueur d'onde 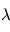$\lambda$ . On sait qu'une fois l'équilibre thermodynamique atteint, ces deux corps en contact radiatif auront la même température 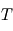. Si l'on note 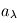$a_{\lambda}$ la fraction du rayonnement incident absorbée par le corps réel, que l'on appelle absorbance, il en renvoie la fraction complémentaire 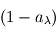$\left( 1 - a_{\lambda} \right)$ . Un bilan net des flux (nul à l'équilibre) à travers le filtre donne alors la relation 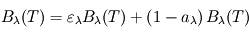$B_{\lambda}(T) = \varepsilon_{\lambda} B_{\lambda}(T) + \left(1 - a_{\lambda} \right) B_{\lambda} (T)$ , ce qui se simplifie en 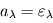$a_{\lambda} = \varepsilon_{\lambda}$ . C'est la loi de Kirchhoff, que L'on résume souvent en "les bons absorbeurs sont les bons émetteurs".

Conséquences

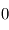Comme l'absorbance est comprise entre et quelle que soit la longueur d'onde, l'émissivité l'est aussi. Il en résulte qu'aucun corps ne peut rayonner plus efficacement que le corps noir à longueur d'onde et température donnée.
Le corps noir ayant par définition une émissivité constante avec la longueur d'onde et égale à , son absorbance est aussi égale à l'unité quelle que soit la longueur d'onde, ce qui justifie son nom de corps noir au sens où il ne réfléchit aucun rayonnement incident.
À l'inverse, un réflecteur parfait qui n'absorberait aucun rayonnement serait également dans l'impossibilité d'émettre quelque rayonnement thermique que ce soit. Une application dans la vie courante de ce phénomène est l'aspect métallique et réfléchissant des objets traités pour éviter les pertes thermiques radiatives : couvertures de survie, bouteilles Thermos : en augmentant leur réflectivité, on abaisse leur absorbance, et donc leur émissivité aussi.