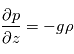La circulation atmosphérique générale
Auteurs: Thomas Navarro, Arianna Piccialli
- Outils
- Coordonnées sphériques
- Forces apparentes
- Force centrifuge
- Force de Coriolis
- Formalisme eulérien ou lagrangien
- Équations de la dynamique
- Les équations primitives
- Les équilibres dynamiques
- Équilibre géostrophique
- Équilibre cyclostrophique
Outils
Auteurs: Thomas Navarro, Arianna Piccialli
Coordonnées sphériques
Comme toute équation de la physique, les équations régissant la dynamique atmosphérique doivent s'exprimer dans un système de coordonnées et un référentiel choisis arbitrairement. Un tel système naturellement adapté à une sphère, et donc à une planète, sont les coordonnées sphériques 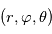 , où
, où 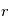 est la distance au centre de la sphère,
est la distance au centre de la sphère, 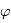 est la l'angle de la longitude, et
est la l'angle de la longitude, et 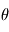 est l'angle de la latitude.
est l'angle de la latitude.
On définit également un repère local pour tout point de l'espace de coordonnées 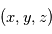 , avec comme base le triplet
, avec comme base le triplet 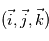 où
où 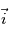 est dirigé vers l'Est,
est dirigé vers l'Est, 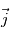 dirigé vers le Nord, et
dirigé vers le Nord, et 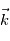 selon la verticale locale vers le haut. Le référentiel d'étude est ce référentiel local, lié à la rotation de la planète, il s'agit donc d'un référentiel tournant, donc non galiléen.
selon la verticale locale vers le haut. Le référentiel d'étude est ce référentiel local, lié à la rotation de la planète, il s'agit donc d'un référentiel tournant, donc non galiléen.
Système de coordonnées sphériques
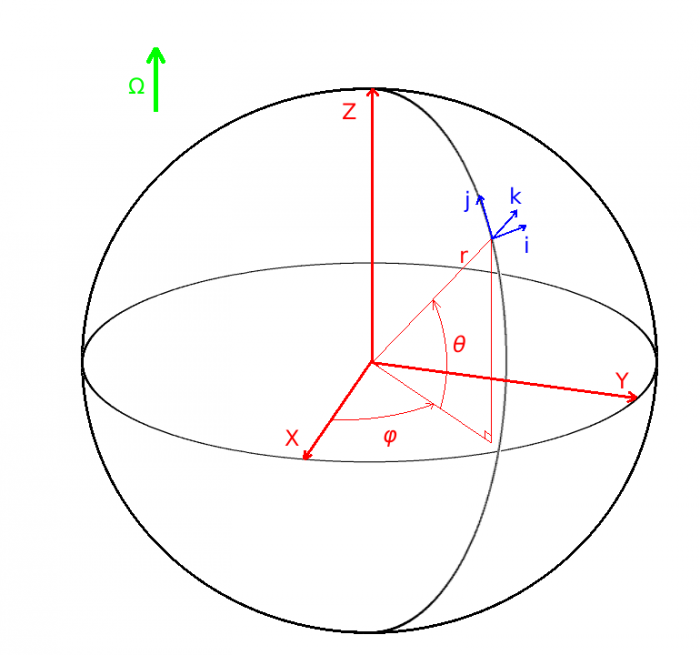
Crédit :
Arianna Piccialli
L'exercice suivant permet de se familiariser avec la manipulation mathématique des coordonnées et des repères. Les resultats serviront à établir l'équation fondamentale de la dynamique.
 Exercice
Exercice
Question 1)
Montrer que dans le référentiel de la planète, un point de coordonnées sphériques 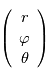 a pour coordonnées cartésiennes
a pour coordonnées cartésiennes 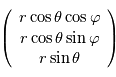
Question 3)
Montrer qu'une vitesse dans le référentiel local 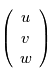 au point de coordonnées sphériques
au point de coordonnées sphériques 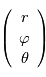 s'exprime par
s'exprime par 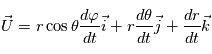 .
.
Forces apparentes
Pour résoudre les équations régissant une atmosphère, on se place dans le référentiel local, lui-même dans un référentiel tournant avec la planète. Ce référentiel n'est pas inertiel, c'est-à-dire qu'il est en accélération par rapport à un référentiel inertiel. Afin de poser le principe fondamental de la dynamique, il est essentiel de tenir de compte de l'accélération apparente du référentiel d'étude, sous la forme de pseudo-forces.
 Précision
Précision
Traditionnellement et pour des raisons pratiques on parle de force, ou pseudo-force, en multipliant l'accélération apparente par la masse de l'objet. On parlera ici plutôt de l'accélération d'une force apparente afin de s'affranchir du terme de masse, qui disparaitra dans les équations finales.
Force centrifuge
 Force centrifuge
Force centrifuge
La force centrifuge est la force apparente due au fait que le référentiel d'étude est en rotation, donc en accélération. En effet, l'orientation de la vitesse d'un point lié à la planète varie, mais pas son module. Ainsi, une particule au repos dans un référentiel galiléen aura une force apparente dans le référentiel de la planète.
On définit le vecteur rotation 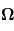 comme étant le vecteur orienté selon l'axe de rotation de la planète et de module
comme étant le vecteur orienté selon l'axe de rotation de la planète et de module 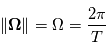 avec
avec 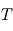 la période de rotation de la planète.
L'accélération de la force centrifuge s'exprime
la période de rotation de la planète.
L'accélération de la force centrifuge s'exprime 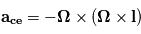 avec
avec 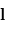 le vecteur position depuis l'axe de rotation où la force s'applique.
Dans un système de coordonnées sphériques, on a
le vecteur position depuis l'axe de rotation où la force s'applique.
Dans un système de coordonnées sphériques, on a 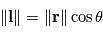 , avec
, avec 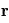 le vecteur position depuis le centre de la planète.
le vecteur position depuis le centre de la planète.
Une autre manière de l'exprimer est de dire qu'il s'agit d'une accélération perpendiculaire à l'axe de rotation, orientée vers l'extérieur et de valeur 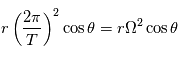
La force centrifuge est regroupée avec la force de gravité, dont l'accélération vaut 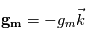 , l'indice
, l'indice 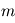 faisant référence à la masse de la planète. On obtient une force dont l'accélération totale est
faisant référence à la masse de la planète. On obtient une force dont l'accélération totale est 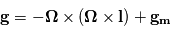 . Cette force dérive d'un potentiel, qu'on appelle le géopotentiel, somme de l'action de la gravité et de la force centrifuge.
. Cette force dérive d'un potentiel, qu'on appelle le géopotentiel, somme de l'action de la gravité et de la force centrifuge.
 Exercices de démonstration et d'acquisition du cours
Exercices de démonstration et d'acquisition du cours
Question 1)
Démontrer par l'analyse ou par un schéma en 3D que 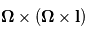 correspond bien à une accélération perpendiculaire à l'axe de rotation, orientée vers l'extérieur et de valeur
correspond bien à une accélération perpendiculaire à l'axe de rotation, orientée vers l'extérieur et de valeur 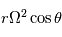 . Comment s'exprime cette accélération dans le référentiel local ?
. Comment s'exprime cette accélération dans le référentiel local ?
Question 2)
Par la suite on fait l'approximation que pour l'accélération due au géopotentiel, on peut se contenter de considérer sa composante uniquement suivant l'axe 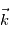 pour l'additionner à la pesanteur, ceci afin de simplifier les équations du problème. Afin de s'assurer que cette approximation reste acceptable, quelle est l'erreur maximale faite dans le cas de la Terre si on ne considère pas les autres composantes de l'accélération due au géopotentiel ? Quelle est cette erreur relativement à l'accélération de pesanteur ? Et pour Jupiter ?
pour l'additionner à la pesanteur, ceci afin de simplifier les équations du problème. Afin de s'assurer que cette approximation reste acceptable, quelle est l'erreur maximale faite dans le cas de la Terre si on ne considère pas les autres composantes de l'accélération due au géopotentiel ? Quelle est cette erreur relativement à l'accélération de pesanteur ? Et pour Jupiter ?
Force de Coriolis
Dans un référentiel en rotation, une autre force apparente est à prendre en compte lors d'un déplacement. Il s'agit de la force de Coriolis, qui tient compte du fait que le déplacement d'une particule génère une accélération apparente supplémentaire. Par exemple, le mouvement rectiligne d'une particule est apparement dévié pour un observateur situé dans un référentiel tournant.
L'accélération de la force de Coriolis s'exprime 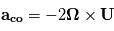 avec
avec 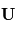 le vecteur vitesse de la parcelle d'air considérée.
le vecteur vitesse de la parcelle d'air considérée.
La vitesse 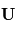 d'une parcelle d'air dans l'atmosphère est généralement orientée parallèlement à la surface locale, c'est-à-dire que sa composante radiale (c'est-à-dire sa composante verticale locale) est en générale petit par rapport à au moins une des deux autres. En négligeant la composante radiale, on constate les choses suivantes :
d'une parcelle d'air dans l'atmosphère est généralement orientée parallèlement à la surface locale, c'est-à-dire que sa composante radiale (c'est-à-dire sa composante verticale locale) est en générale petit par rapport à au moins une des deux autres. En négligeant la composante radiale, on constate les choses suivantes :
- A l'équateur l'accélération de Coriolis est orientée selon l'axe radial, c'est-à-dire vers le haut ou vers le bas.
- Dans l'hémisphère Nord, sa projection sur le plan de la surface locale est orientée à droite du vecteur vitesse
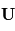
- Dans l'hémisphère Sud, sa projection sur le plan de la surface locale est orientée à gauche du vecteur vitesse
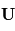
Ceci explique pourquoi certaines structures atmosphériques, tels les ouragans ou les anticyclones, tournent toujours dans le sens des aiguilles d'une montre dans l'hémisphère Nord, et dans le sens contraire dans l'autre hémisphère.
 Exercice de démonstration et d'acquisition du cours
Exercice de démonstration et d'acquisition du cours
Question 1)
Démontrer par l'analyse ou par un schéma en 3D les 3 points ci-dessus.
Formalisme eulérien ou lagrangien
Les écoulements atmosphériques peuvent être décrits en utilisant deux points de vue classiques, appelés eulérien ou lagrangien :
 Description eulérienne
Description eulérienne
L'écoulement est suivi par un observateur depuis une position fixe. C'est le cas, par exemple, d'un atterrisseur sur Mars fixé au sol qui mesure la vitesse du vent, la température, ou la pression. Cette description est souvent préférée car elle est la plus pratique.
 Description lagrangienne
Description lagrangienne
Dans ce cas, les particules fluides sont suivies le long de leurs trajectoires. C'est la description la plus intuitive.
Équations de la dynamique
 Exercice
Exercice
Question 1)
Comment s'exprime l'accélération de la force de Coriolis 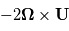 dans le repère local ?
dans le repère local ?
C'est le même exercice que celui sur la force de Coriolis, mais sans négliger la composante 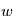 .
.
 Exercice
Exercice
Question 1)
Déduire les équations de Navier-Stokes en coordonnées sphériques données ci-dessus à partir de l'équation fondamentale de la dynamique (Equation 1).
Les équations primitives
 Approximations
Approximations
Les équations de la dynamique sont très compliquées car elles forment un système non linéaire. Ceci signifie que la somme de deux solutions n'est pas forcément solution du problème, ce qui rend la résolution de ces équations très ardue, et à ce jour encore source de recherches. Cependant, en fonction des phénomènes étudiés et des caractéristiques de l'atmosphère planétaire, certains termes de ces équations peuvent en dominer d'autres. Pour estimer les différents termes dans les équations, on utilise la méthode de l'analyse d'échelle. Les ordres de grandeur des différents termes en jeu dans les équations fondamentales de la dynamique seront très différents selon l'échelle des écoulements que l'on souhaite étudier. Dans le tableau ci-dessous on compare les termes dominants sur les planètes à rotation rapide (la Terre) avec ceux sur les planètes à rotation lente (Vénus):
Termes dominants dans les équations de la dynamique
| 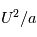 | 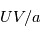 | 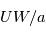 | 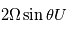 | 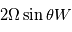 | 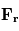 |
| Terre | 10-5 | 10-5 | 10-8 | 10-3 | 10-6 | 10-12 |
| Vénus | 10-3 | 10-5 | 10-5 | 10-5 | 10-7 | 10-12 |
avec 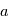 le rayon de la planète. On a
le rayon de la planète. On a 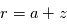 , où
, où 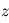 est l'altitude depuis la surface.
est l'altitude depuis la surface.
On peut alors appliquer les approximations suivantes:
- L'épaisseur verticale de l'atmosphère est petite par rapport au le rayon de la planète. Par conséquence, on remplace la distance
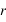 au centre de la planète par le rayon de la planète
au centre de la planète par le rayon de la planète 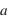 avec une erreur négligeable. Dans ce cas, les dérivées
avec une erreur négligeable. Dans ce cas, les dérivées 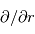 deviennent
deviennent 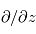 où
où 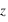 est l'altitude.
est l'altitude. - Les trois composantes du terme de friction moléculaire
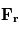 ont un ordre de grandeur de 10-12 m s-2 et peuvent être négligées pour tous les écoulements, sauf pour les mouvements turbulents à petite échelle près du sol.
ont un ordre de grandeur de 10-12 m s-2 et peuvent être négligées pour tous les écoulements, sauf pour les mouvements turbulents à petite échelle près du sol. - Les vitesses verticales sont beaucoup plus petites que les vitesses horizontales, donc on néglige tous les termes contenant
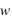 .
. - Dans le cas de mouvements à grande échelle, on suppose l'équilibre hydrostatique :
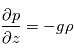
On obtient alors les équations primitives de la météorologie :
 Equilibre hydrostatique vertical:
Equilibre hydrostatique vertical:
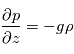
À ce système d'équations on ajoute l'équation des gaz parfaits:
ainsi que l'équation de conservation de la masse:
 Equation de continuité:
Equation de continuité:
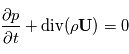
Enfin, le premier principe de la thermodynamique:
On obtient ainsi 6 équations avec 6 inconnues (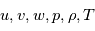 ).
).
Ce système d'équations primitives est le plus complet utilisé pour l'étude de la circulation générale de l'atmosphère. C'est notamment celui utilisé par les modèles de circulation générale.
Les équilibres dynamiques
Équilibre géostrophique
Les équilibres géostrophique et cyclostrophique sont deux approximations des équations primitives. Ils sont purement diagnostiques : ils ne contiennent pas de dérivées dans le temps, d'où l'impossibilité de faire des prédictions. Néanmoins, ils sont des outils puissants pour décrire différents écoulements observés dans les planètes.
 L'équilibre géostrophique
L'équilibre géostrophique
L'approximation géostrophique est un développement des équations primitives utilisée aux moyennes latitudes sur les planètes à rotation rapide (Terre, Mars). On suppose l'équilibre entre la force de Coriolis et la force due au gradient horizontal de pression. La force centrifuge est négligée.
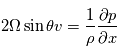
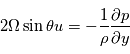
D'après ces équations, lorsque cet équilibre est valide, la vitesse du vent est directement proportionnelle au gradient horizontal de pression. Notez que l'équilibre géostrophique cesse d'être valide autour des latitudes équatoriales.
Force en action en équilibre géostrophique
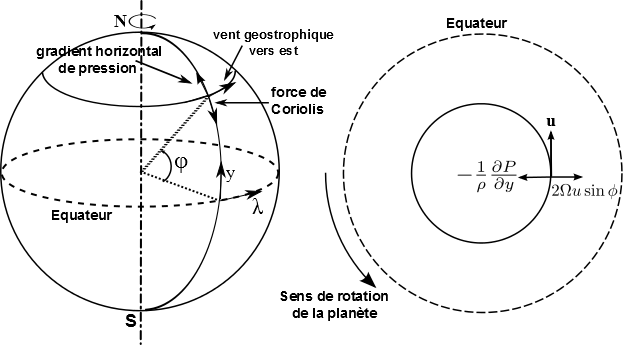
Crédit :
Arianna Piccialli
 Vent géostrophique
Vent géostrophique
En combinant les deux composantes de la vitesse, on peut introduir le vent géostrophique comme :
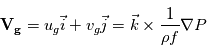
Équilibre cyclostrophique
 L'équilibre cyclostrophique
L'équilibre cyclostrophique
La circulation générale des planètes à rotation lente (Vénus, Titan), aussi bien que les vortex et les tourbillons sur toutes les planètes, peut être approximée par l'équilibre cyclostrophique. Cela suppose l'égalité entre la composante dirigée vers l'équateur de la force centrifuge et le gradient méridional de la pression. La force de Coriolis est négligée.
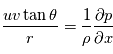
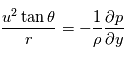
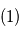
Forces en action en équilibre cyclostrophique
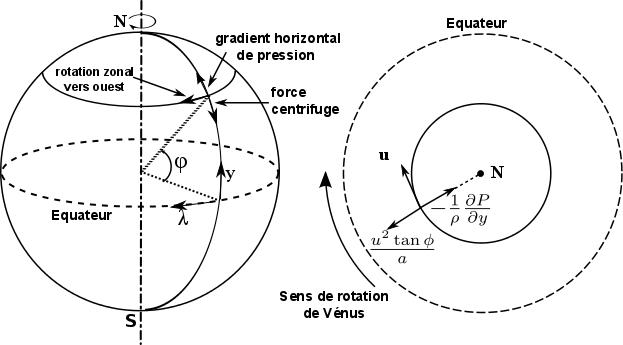
Crédit :
Arianna Piccialli, adaptation de Schubert, 1983.
 Vent cyclostrophique
Vent cyclostrophique
L'équation du vent cyclostrophique peut alors être écrite comme :
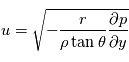
 Exercice
Exercice
Réponses aux exercices
pages_fluide-dynamique/coord-sphere.html
Exercice
pages_fluide-dynamique/equations-dynamique.html
Exercice
pages_fluide-dynamique/equations-dynamique.html
Exercice
pages_fluide-dynamique/equilibres-dynamiques.html
Exercice
- Question 1
Aide :
- Utiliser la loi des gaz parfaits
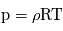
- La définition de géopotentiel :
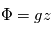 , avec
, avec 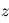 la hauteur et
la hauteur et 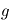 l'accélération gravitationnelle
l'accélération gravitationnelle - L'approximation hydrostatique :
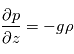
 , où
, où 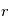 est la distance au centre de la sphère,
est la distance au centre de la sphère, 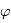 est la l'angle de la longitude, et
est la l'angle de la longitude, et 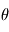 est l'angle de la latitude.
est l'angle de la latitude.
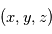 , avec comme base le triplet
, avec comme base le triplet 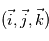 où
où 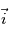 est dirigé vers l'Est,
est dirigé vers l'Est, 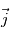 dirigé vers le Nord, et
dirigé vers le Nord, et 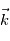 selon la verticale locale vers le haut. Le référentiel d'étude est ce référentiel local, lié à la rotation de la planète, il s'agit donc d'un référentiel tournant, donc non galiléen.
selon la verticale locale vers le haut. Le référentiel d'étude est ce référentiel local, lié à la rotation de la planète, il s'agit donc d'un référentiel tournant, donc non galiléen.
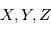 ).
).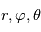 ).
).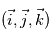 , qui est un système de coordonnées cartésiennes.
, qui est un système de coordonnées cartésiennes. Exercice
Exercice a pour coordonnées cartésiennes
a pour coordonnées cartésiennes 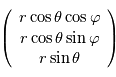
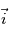 ,
, 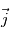 et
et 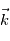 dans le repère de la planète en fonction des angles
dans le repère de la planète en fonction des angles 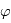 et
et 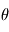
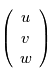 au point de coordonnées sphériques
au point de coordonnées sphériques  s'exprime par
s'exprime par 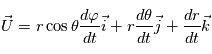 .
.
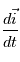 ,
, 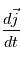 et
et 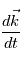 en fonction de
en fonction de 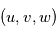 ,
, 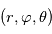 et
et 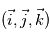 .
.

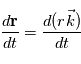 en gardant en tête que
en gardant en tête que 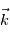 est un vecteur local qui dépend de la position, donc varie avec les coordonnées
est un vecteur local qui dépend de la position, donc varie avec les coordonnées 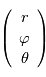 .
.
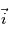 ,
, 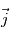 et
et 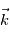 en fonction des angles
en fonction des angles 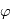 et
et 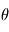 .
.
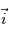 ,
, 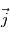 ,
, 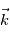 ,
, 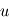 ,
, 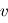 et
et 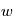 .
.
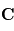 des vecteurs
des vecteurs 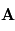 et
et 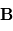 s'écrit
s'écrit 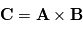 et correspond au vecteur orthogonal à la fois à
et correspond au vecteur orthogonal à la fois à  et
et 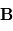 tel que le triplet
tel que le triplet 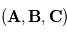 soit de sens direct. et que le module du produit soit
soit de sens direct. et que le module du produit soit 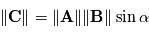 où
où 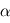 est l'angle direct de
est l'angle direct de 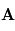 vers
vers 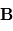 . Ainsi, si
. Ainsi, si 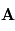 et
et 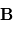 sont colinéaires, leur produit vectoriel sera le vecteur nul.
sont colinéaires, leur produit vectoriel sera le vecteur nul.
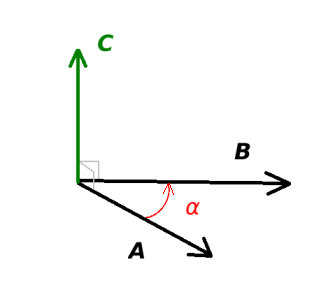
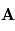 ,
, 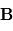 et
et  forment une base directe puisque
forment une base directe puisque 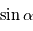 est positif. Si
est positif. Si 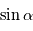 était négatif, la base serait dans le sens indirect.
était négatif, la base serait dans le sens indirect.
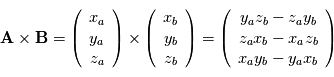
 comme étant le vecteur orienté selon l'axe de rotation de la planète et de module
comme étant le vecteur orienté selon l'axe de rotation de la planète et de module 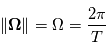 avec
avec 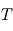 la période de rotation de la planète.
L'accélération de la force centrifuge s'exprime
la période de rotation de la planète.
L'accélération de la force centrifuge s'exprime 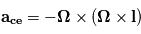 avec
avec 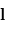 le vecteur position depuis l'axe de rotation où la force s'applique.
Dans un système de coordonnées sphériques, on a
le vecteur position depuis l'axe de rotation où la force s'applique.
Dans un système de coordonnées sphériques, on a 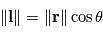 , avec
, avec 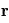 le vecteur position depuis le centre de la planète.
le vecteur position depuis le centre de la planète.
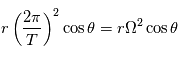
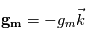 , l'indice
, l'indice 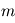 faisant référence à la masse de la planète. On obtient une force dont l'accélération totale est
faisant référence à la masse de la planète. On obtient une force dont l'accélération totale est 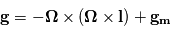 . Cette force dérive d'un potentiel, qu'on appelle le géopotentiel, somme de l'action de la gravité et de la force centrifuge.
. Cette force dérive d'un potentiel, qu'on appelle le géopotentiel, somme de l'action de la gravité et de la force centrifuge.
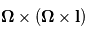 correspond bien à une accélération perpendiculaire à l'axe de rotation, orientée vers l'extérieur et de valeur
correspond bien à une accélération perpendiculaire à l'axe de rotation, orientée vers l'extérieur et de valeur 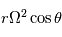 . Comment s'exprime cette accélération dans le référentiel local ?
. Comment s'exprime cette accélération dans le référentiel local ?
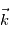 pour l'additionner à la pesanteur, ceci afin de simplifier les équations du problème. Afin de s'assurer que cette approximation reste acceptable, quelle est l'erreur maximale faite dans le cas de la Terre si on ne considère pas les autres composantes de l'accélération due au géopotentiel ? Quelle est cette erreur relativement à l'accélération de pesanteur ? Et pour Jupiter ?
pour l'additionner à la pesanteur, ceci afin de simplifier les équations du problème. Afin de s'assurer que cette approximation reste acceptable, quelle est l'erreur maximale faite dans le cas de la Terre si on ne considère pas les autres composantes de l'accélération due au géopotentiel ? Quelle est cette erreur relativement à l'accélération de pesanteur ? Et pour Jupiter ?
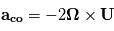 avec
avec 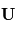 le vecteur vitesse de la parcelle d'air considérée.
le vecteur vitesse de la parcelle d'air considérée.
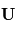 d'une parcelle d'air dans l'atmosphère est généralement orientée parallèlement à la surface locale, c'est-à-dire que sa composante radiale (c'est-à-dire sa composante verticale locale) est en générale petit par rapport à au moins une des deux autres. En négligeant la composante radiale, on constate les choses suivantes :
d'une parcelle d'air dans l'atmosphère est généralement orientée parallèlement à la surface locale, c'est-à-dire que sa composante radiale (c'est-à-dire sa composante verticale locale) est en générale petit par rapport à au moins une des deux autres. En négligeant la composante radiale, on constate les choses suivantes :
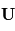
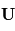
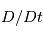 . Soit
. Soit ![\textbf{A}[\textbf{r}(t)]](../pages_fluide-dynamique/equations_outils/equation166.png) une grandeur physique vectorielle de l'écoulement, dépendant du point d'observation
une grandeur physique vectorielle de l'écoulement, dépendant du point d'observation 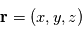 et du temps
et du temps 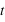 . La variation de la grandeur
. La variation de la grandeur 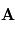 s'écrit :
s'écrit :
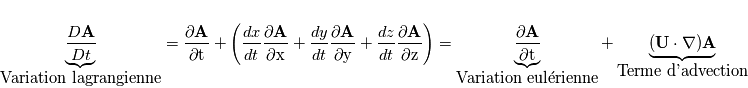
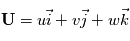 est la vitesse du fluide avec composants:
est la vitesse du fluide avec composants: 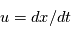 ,
, 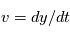 ,
, 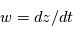 .
.
![f[\textbf{r}(t)]](../pages_fluide-dynamique/equations_outils/equation175.png) , la relation est la même.
, la relation est la même.
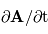 décrit la variation locale avec le temps en un point d'observation fixé (point de vue eulérien) .
décrit la variation locale avec le temps en un point d'observation fixé (point de vue eulérien) .
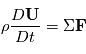 avec
avec 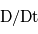 est la
est la 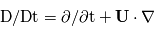 ,
, 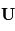 la vitesse du fluide,
la vitesse du fluide, 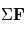 la somme des forces s'appliquant sur la parcelle et
la somme des forces s'appliquant sur la parcelle et 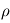 la densité du fluide.
la densité du fluide.
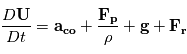
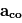 l'accélération de la
l'accélération de la 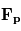 les forces dues au gradient de pression,
les forces dues au gradient de pression, 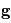 l'accélération du
l'accélération du 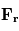 qui désigne l'accélération dues à la viscosité. Ce qui donne :
qui désigne l'accélération dues à la viscosité. Ce qui donne :
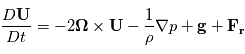 (1)
(1)
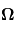 est le vecteur de rotation de la planète
est le vecteur de rotation de la planète 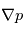 est le gradient de pression.
est le gradient de pression.
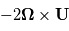 dans le repère local ?
dans le repère local ?
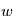 .
.
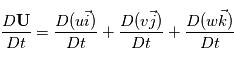 . Or
. Or 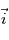 ,
,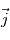 et
et 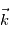 . Ceci nous permet d'établir les équations de Navier-Stokes dans le référentiel local, en notant que
. Ceci nous permet d'établir les équations de Navier-Stokes dans le référentiel local, en notant que 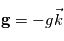 et
et 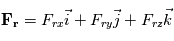 :
:

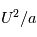
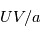
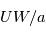
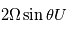
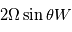
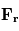
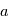 le rayon de la planète. On a
le rayon de la planète. On a 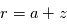 , où
, où 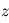 est l'altitude depuis la surface.
est l'altitude depuis la surface.
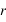 au centre de la planète par le rayon de la planète
au centre de la planète par le rayon de la planète 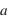 avec une erreur négligeable. Dans ce cas, les dérivées
avec une erreur négligeable. Dans ce cas, les dérivées 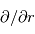 deviennent
deviennent 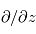 où
où 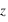 est l'altitude.
est l'altitude.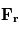 ont un ordre de grandeur de 10-12 m s-2 et peuvent être négligées pour tous les écoulements, sauf pour les mouvements turbulents à petite échelle près du sol.
ont un ordre de grandeur de 10-12 m s-2 et peuvent être négligées pour tous les écoulements, sauf pour les mouvements turbulents à petite échelle près du sol.  .
.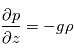
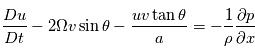
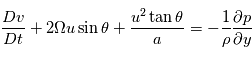
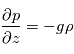
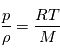
 la constante universelle des gaz parfaits et
la constante universelle des gaz parfaits et 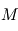 la masse molaire du gaz qui constitue l'atmosphère, et dépend donc de sa composition. Pour l'air terrestre, on a
la masse molaire du gaz qui constitue l'atmosphère, et dépend donc de sa composition. Pour l'air terrestre, on a 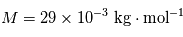
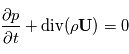
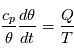
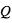 le forçage diabatique et
le forçage diabatique et 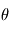 la température potentielle :
la température potentielle : ![\theta=T\left[\frac{p_0}{p}\right]^{\kappa}](../pages_fluide-dynamique/equations_circulation-generale/equation230.png) , où
, où 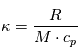 ,
, 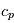 la chaleur spécifique à pression constante et
la chaleur spécifique à pression constante et 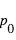 une pression de référence.
une pression de référence.
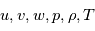 ).
).
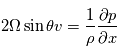
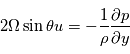

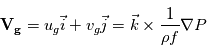
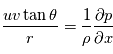
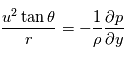

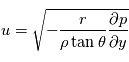
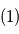 que l'équation du vent cyclostrophique peut être écrite comme :
que l'équation du vent cyclostrophique peut être écrite comme :
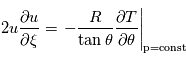
 J kg-1 K-1, et
J kg-1 K-1, et 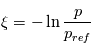 est la coordonnée de pression logarithmique, avec
est la coordonnée de pression logarithmique, avec 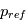 la pression au niveau de référence.
la pression au niveau de référence.
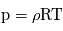
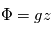 , avec
, avec 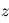 la hauteur et
la hauteur et 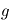 l'accélération gravitationnelle
l'accélération gravitationnelle