Équations de la dynamique

Auteurs: Thomas Navarro, Arianna Piccialli

L'équation fondamentale de la dynamique

Le mouvement d'une particule dans un fluide est décrit par la deuxième loi de Newton (conservation de la quantité de mouvement) qui lorsqu'elle est appliquée à la mécanique des fluides donne l'équation de Navier-Stokes. Dans un système en rotation l'équation du mouvement d'une parcelle de fluide est:

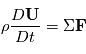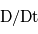$\rho\frac{D\mathbf{U}}{Dt}=\Sigma\mathbf{F}$ avec $\mathrm{D}/\mathrm{Dt}$ est la dérivée particulaire qui s'écrit 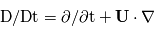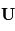$\mathrm{D}/\mathrm{Dt}={\partial{}}/\partial{\mathrm{t}}+\mathbf{U}\cdot{\nabla}$ , $\mathbf{U}$ la vitesse du fluide, 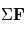$\Sigma\mathbf{F}$ la somme des forces s'appliquant sur la parcelle et 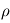$\rho$ la densité du fluide.

Soit en détaillant les forces :

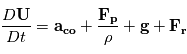
$\frac{D\mathbf{U}}{Dt}=\mathbf{a_{co}}+\frac{\mathbf{F_{p}}}{\rho}+\mathbf{g}+\mathbf{F_r}$

avec 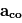$\mathbf{a_{co}}$ l'accélération de la force de Coriolis, 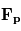$\mathbf{F_p}$ les forces dues au gradient de pression, 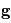$\mathbf{g}$ l'accélération du géopotentiel, et 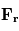$\mathbf{F_r}$ qui désigne l'accélération dues à la viscosité. Ce qui donne :

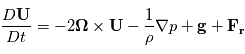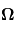$\frac{D\mathbf{U}}{Dt}=-2\mathbf{\Omega}\times\mathbf{U}-\frac{1}{\rho}\nabla{p}+\mathbf{g}+\mathbf{F_r}$ (1)

où $\mathbf{\Omega}$ est le vecteur de rotation de la planète 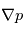$\nabla{p}$ est le gradient de pression.

Exercice

Question 1)

Comment s'exprime l'accélération de la force de Coriolis 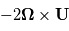$-2\mathbf{\Omega}\times\mathbf{U}$ dans le repère local ?

Aide

Les équations en coordonnées sphériques

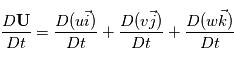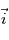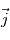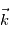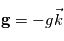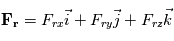On a $\frac{D\mathbf{U}}{Dt} = \frac{D(u\vec i)}{Dt} + \frac{D(v\vec j)}{Dt} + \frac{D(w\vec k)}{Dt}$ . Or il a été vu en exercice les expressions des dérivées temporelles des vecteurs $\vec i$ , $\vec j$ et $\vec k$ . Ceci nous permet d'établir les équations de Navier-Stokes dans le référentiel local, en notant que $\mathbf{g}=-g\vec k$ et $\mathbf{F_r}=F_{rx}\vec i + F_{ry}\vec j +F_{rz}\vec k$ :

Le survol de la souris sur chaque terme des équations de Navier-Stokes donne son origine.

Ce système d'équations décrit tous les types de mouvements atmosphériques à toutes les échelles. Ces équations sont compliquées à résoudre, mais dans bien des cas utiliser une approximation est suffisante pour modéliser de nombreux phénomènes atmosphériques dynamiques.

Exercice

Question 1)

Déduire les équations de Navier-Stokes en coordonnées sphériques données ci-dessus à partir de l'équation fondamentale de la dynamique (Equation 1).

Aide