Les équations primitives

Auteurs: Thomas Navarro, Arianna Piccialli

Approximations

Les équations de la dynamique sont très compliquées car elles forment un système non linéaire. Ceci signifie que la somme de deux solutions n'est pas forcément solution du problème, ce qui rend la résolution de ces équations très ardue, et à ce jour encore source de recherches. Cependant, en fonction des phénomènes étudiés et des caractéristiques de l'atmosphère planétaire, certains termes de ces équations peuvent en dominer d'autres. Pour estimer les différents termes dans les équations, on utilise la méthode de l'analyse d'échelle. Les ordres de grandeur des différents termes en jeu dans les équations fondamentales de la dynamique seront très différents selon l'échelle des écoulements que l'on souhaite étudier. Dans le tableau ci-dessous on compare les termes dominants sur les planètes à rotation rapide (la Terre) avec ceux sur les planètes à rotation lente (Vénus):

Termes dominants dans les équations de la dynamique
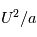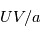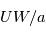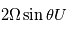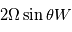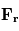				$2\Omega\sin\theta{U}$	$2\Omega\sin\theta{W}$	$\mathbf{F_r}$
Terre	10^-5	10^-5	10^-8	10^-3	10^-6	10^-12
Vénus	10^-3	10^-5	10^-5	10^-5	10^-7	10^-12

avec 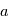le rayon de la planète. On a 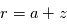r=a+z , où 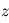est l'altitude depuis la surface.

On peut alors appliquer les approximations suivantes:

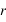L'épaisseur verticale de l'atmosphère est petite par rapport au le rayon de la planète. Par conséquence, on remplace la distance au centre de la planète par le rayon de la planète 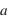avec une erreur négligeable. Dans ce cas, les dérivées 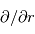$\partial}/{\partial{r}$ deviennent 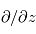$\partial}/{\partial{z}$ où 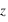est l'altitude.
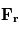Les trois composantes du terme de friction moléculaire $\mathbf{F_r}$ ont un ordre de grandeur de 10^-12m s^-2et peuvent être négligées pour tous les écoulements, sauf pour les mouvements turbulents à petite échelle près du sol.
Les vitesses verticales sont beaucoup plus petites que les vitesses horizontales, donc on néglige tous les termes contenant .
Dans le cas de mouvements à grande échelle, on suppose l'équilibre hydrostatique :

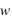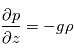
$\frac{\partial{p}}{\partial{z}}=-g\rho$

On obtient alors les équations primitives de la météorologie :

Mouvement horizontal:

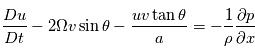
$\frac{Du}{Dt}-2\Omega{v}\sin\theta-\frac{uv\tan\theta}{a}=-\frac{1}{\rho}\frac{\partial{p}}{\partial{x}}$

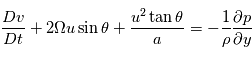
$\label{Navier_stokes_2}\frac{Dv}{Dt}+2\Omega{u}\sin\theta+\frac{u^2\tan\theta}{a}=-\frac{1}{\rho}\frac{\partial{p}}{\partial{y}}$

Equilibre hydrostatique vertical:

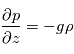
$\frac{\partial{p}}{\partial{z}}=-g\rho$

À ce système d'équations on ajoute l'équation des gaz parfaits:

Equation d'état:

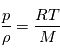
$\frac{p}{\rho} = \frac{RT}{M}$

Avec 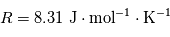$R=8.31~ \mathrm{J}\cdot \mathrm{mol}^{-1}\cdot \mathrm{K}^{-1}$ la constante universelle des gaz parfaits et 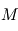la masse molaire du gaz qui constitue l'atmosphère, et dépend donc de sa composition. Pour l'air terrestre, on a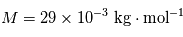 $M = 29\times10^{-3}~ \mathrm{kg}\cdot \mathrm{mol}^{-1}$

ainsi que l'équation de conservation de la masse:

Equation de continuité:

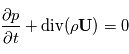
$\frac{\partial{p}}{\partial{t}}+\mathrm{div}(\rho\mathbf{U})=0$

Enfin, le premier principe de la thermodynamique:

Premier principe de la thermodynamique:

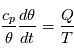
$\frac{c_p}{\theta}\frac{d\theta}{dt}=\frac{Q}{T}$

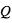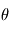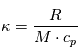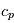Avec le forçage diabatique et $\theta$ la température potentielle : $\theta=T\left[\frac{p_0}{p}\right]^{\kappa}$ , où $\kappa=\frac{R}{M\cdot c_p}$ , c_p la chaleur spécifique à pression constante et 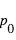p_0 une pression de référence.

On obtient ainsi 6 équations avec 6 inconnues (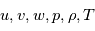 $u,v,w,p,\rho,T$ ).

Ce système d'équations primitives est le plus complet utilisé pour l'étude de la circulation générale de l'atmosphère. C'est notamment celui utilisé par les modèles de circulation générale.