Boite à outils
Auteur: Françoise Roques
- Appliquettes
- Notions de base
- Les notions de base
- Gravitation et lois de Kepler
- Résonances
- Etoile ou planète?
- La système solaire
- Loi de Planck -Emission du corps noir-Loi de Stefan-Boltzmann
- Température d'équilibre d'une planète
- Diagramme Hertzsprung-Russel
Boite à outils
Cette boite à outils contient :
Appliquettes
Auteurs: Cédric Schott, Pierre-Yves Martin
Appliquettes
Appliquettes interactives
Voilà une liste des outils réalisés dans le cadre du projet SESP, réalisés par Cédric Schott et Pierre-Yves Martin. Ils sont tous distribués sous une licence libre (GNU GPL).
Modèle radiatif à 2 couches d'une atmosphère Emmanuel Marcq (LATMOS)
Flux & Spectre - Transmission Emmanuel Marcq (LATMOS)
-
Résultats 2D-3D d'un GCM Thomas Navarro, François Forget (LMD)
GCM 1D interactif, avec évolution des paramètres en temps réel. Martin Turbert, Benjamin Charnay, François Forget (LMD)
-
Equations de Navier-Stoke, Arianna Piccialli (LESIA)
Brillance d'un day glow en fonction de la longueur d'onde et de l'altitude, Jean-Yves Chaufray (LATMOS)
Brillance d'un night glow en fonction de la longueur d'onde et de l'altitude, Jean-Yves Chaufray (LATMOS)
La loi des grands nombres
Equipartition - Lancer d'une pièce
Vitesse radiale - Transit - HD 189733 (Bouchy et al. 2005) Jean-Mathias Griessmeier (LPC2E)
Transit - Flux relatif - HD 189733b (Knutson et al. 2007) Jean-Mathias Griessmeier (LPC2E)
Calcul de cratérisation, Alice Le Gall (LATMOS)
-
Ségrégation thermique à la surface d'un corps Alice Le Gall (LATMOS)
-
Erosion - Mise en mouvement des sédiments sur Vénus, la Terre, Mars et Titan Alice Le Gall (LATMOS)
Sonde de Langmuir Ronan Modolo (LATMOS)
Sondes de Langmuir - Cassini Ronan Modolo (LATMOS)
Polarisation - Diffusion de Mie Loic Rossi (LATMOS)
Catalogue site Les Exoplanètes
Diagrammes 4 paramètres:site Les Exoplanètes
Histogrammes site Les Exoplanètes
Carte 2D : site Les Exoplanètes
Carte 3D : site Les Exoplanètes
Simulateur d'orbite 3D : site Les Exoplanètes
Compteur d'exoplanètes site Les Exoplanètes
Tableau site Les Exoplanètes
-
Table des systèmes site Les Exoplanètes
Equation de Drake site Les Exoplanètes
Notions de base
Auteur: Françoise Roques
Les notions de base
L'étude des systèmes planétaires du Soleil ou des autres étoiles s'appuie sur quelques notions importantes qui sont décrites ci-dessous :
Gravitation et lois de Kepler
Les lois de Kepler (1571-1630) ont été établies empiriquement à partir des observations détaillées du mouvement de Venus, Mars, Jupiter et Saturne par Tycho Brahe (1546-1601). Les 2 premières lois ont été publiées en 1609 dans Astronomia Nova, la troisième a été publiée en 1619 dans Harmonices Mundi. Elles ne furent démontrées mathématiquement que par la suite, par Isaac Newton (1642-1727)
Les 3 lois de Kepler, bien qu’antérieures à la théorie de Newton, résultent de la loi de la gravitation universelle qui postule que 2 masses 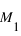 et
et 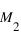 séparées d’une distance R exercent l’une sur l’autre une force attractive parallèle au rayon vecteur qui joint leurs centres de masse respectifs. Cette force s’exprime par la relation :
séparées d’une distance R exercent l’une sur l’autre une force attractive parallèle au rayon vecteur qui joint leurs centres de masse respectifs. Cette force s’exprime par la relation :
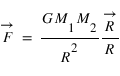
avec G constante universelle de la gravitation = 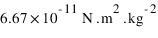
Les lois de Kepler sont toujours vraies pour un système à 2 corps mais restent valables pour des systèmes multiples (plusieurs planètes) dans l’approximation de faible masse des planètes par rapport à l’étoile centrale. Elles ont été énoncées pour le Système Solaire, mais peuvent donc être généralisées à tout système planétaire dont les planètes ont une masse petite devant celle de l'étoile. Mais attention, ce n'est pas le cas de tous les systèmes exoplanétaires!
La première loi, dite loi des orbites, (1605), stipule que dans le référentiel héliocentrique, l’orbite de chaque planète est une ellipse dont l’un des foyers est occupé par le Soleil.
La seconde loi, dite loi des aires (1604), stipule que le mouvement de chaque planète est tel que le segment de droite reliant le Soleil et la planète balaie des aires égales pendant des durées égales.
La troisième loi, dite loi des périodes (1618) stipule que pour toutes les planètes du système, le rapport entre le cube du demi grand axe a de la trajectoire et le carré de la période orbitale T est constant, c'est à dire a la même valeur pour toutes les planètes du système :
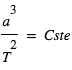
Si a est exprimé en unités astronomiques et T en années terrestres, la constante vaut 1 dans le système solaire.
La loi de la gravitation ci-dessus permet de calculer la valeur de cette constante et de voir que les équations de Kepler font l'approximation que la masse des planètes est négligeable devant la masse de l'étoile:
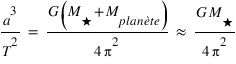
où 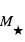 et
et 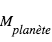 sont respectivement les masses de l’étoile et de la planète.
sont respectivement les masses de l’étoile et de la planète.
Résonances
Quand un système oscillant est soumis à une excitation (perturbation périodique), il peut subir une augmentation de son énergie d’oscillation. Ce phénomène, appelé résonance, dépend des fréquences d’excitation et des fréquences propres du système.
On parle de résonances orbitales quand le phénomène est le mouvement d’une planète autour d’une étoile (ou d’un satellite autour d’une planète). L’excitation est la perturbation gravitationnelle d’une autre planète (d’un autre satellite).
Plusieurs paramètres dans une orbite elliptique de planète, peuvent donner lieu à des résonances :
- Le principal est le mouvement de la planète le long de son orbite. La vitesse moyenne est n, le « moyen mouvement ». Une résonance de moyen mouvement a lieu si les moyens mouvements des deux planètes, n1 et n2 sont dans un rapport rationnel, c’est à dire si :
p.n1 + q.n2 est proche de 0, p et q étant des nombres entiers.
Cette configuration est très courante dans le système solaire. par exemple, :
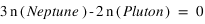
Cette configuration peut concerner plusieurs objets. Ainsi les satellites de Saturne, Io, Europe et Ganymède sont liés par la relation :
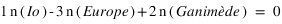
Les résonances peuvent aboutir à un effet paradoxal : Ainsi, malgré que la gravitation soit une force d’attraction, l’accumulation des résonances peut aboutir à un effet de répulsion. Quand un corps orbite dans un anneau/ un disque, les particules de l’anneau sont soumises à une accumulation de résonances d’ordres de plus en plus élévés en s’approchant du corps. L’effet conjugué de ces résonances est une force de répulsion qui éloigne le bord de l’anneau de l’orbite du corps.
- Des résonances peuvent aussi lier le moyen mouvement d’un corps et sa rotation sur lui-même. Un exemple spectaculaire est la rotation synchrone de beaucoup de satellites de planètes et, en particulier, de la Lune. Le moyen mouvement de la Lune autour de la Terre est égal à sa vitesse de rotation sur elle-même, ce qui fait qu’elle présente toujours la même face à la Terre. Les effets de marées ont créé dans la Lune des forces de frottement qui ont ralenti sa rotation jusqu’à la rotation synchrone, configuration qui fait disparaître les frottements.
- Des résonances peuvent aussi lier les mouvements des périapses ou des nœuds ascendants. Ces résonances sont dites «séculaires « parce que ces mouvements sont plus lents que le moyen mouvement,
Etoile ou planète?
En schématisant, nous pouvons dire que la physique de ces objets est principalement gouvernée par leur masse, qui intervient à 2 niveaux :
- la gravitation qui tend à comprimer l’objet, en libérant de l’énergie gravitationnelle
- les processus nucléaires qui s’amorcent, au fur et à mesure que la température augmente au cœur de l’objet.
La masse est ainsi un très bon paramètre pour classifier les différents objets astrophysiques, l’unité de comparaison étant la masse solaire (notée 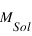 ). On distingue alors, par masse décroissante, 3 catégories d’objets :
). On distingue alors, par masse décroissante, 3 catégories d’objets :
- Si M > 0.08
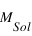 (∼80
(∼80 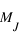 où
où 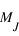 est la masse de Jupiter) la masse est suffisante pour que la contraction gravitationnelle permette d’atteindre au cœur de l’objet la température d’amorçage de la réaction de fusion de l’hydrogène. L’objet est alors appelé « étoile » et son rayon est proportionnel à sa masse
est la masse de Jupiter) la masse est suffisante pour que la contraction gravitationnelle permette d’atteindre au cœur de l’objet la température d’amorçage de la réaction de fusion de l’hydrogène. L’objet est alors appelé « étoile » et son rayon est proportionnel à sa masse - Si 0.013
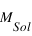 < M < 0.08
< M < 0.08 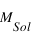 (13
(13 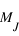 < M < 80
< M < 80 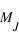 ), la température au cœur de l’objet ne permet pas l’amorçage de la réaction de fusion de l’hydrogène, mais permet l’amorçage de la réaction de fusion du deutérium. L’objet est appelé « naine brune » et son rayon est inversement proportionnel à la racine cubique de sa masse.
), la température au cœur de l’objet ne permet pas l’amorçage de la réaction de fusion de l’hydrogène, mais permet l’amorçage de la réaction de fusion du deutérium. L’objet est appelé « naine brune » et son rayon est inversement proportionnel à la racine cubique de sa masse. - Si M < 0.013
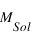 (M < 13
(M < 13 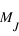 ) la température au cœur de l’objet ne permet pas l’amorçage des réactions de fusion nucléaire. L’objet est appelé « planète ». Au sein de cette catégorie, on distingue généralement les planètes géantes gazeuses des planètes telluriques pour lesquelles la masse n’est pas suffisante pour accréter du gaz. La limite entre planète géante et planète tellurique se situe à environ quelques masses terrestres.
) la température au cœur de l’objet ne permet pas l’amorçage des réactions de fusion nucléaire. L’objet est appelé « planète ». Au sein de cette catégorie, on distingue généralement les planètes géantes gazeuses des planètes telluriques pour lesquelles la masse n’est pas suffisante pour accréter du gaz. La limite entre planète géante et planète tellurique se situe à environ quelques masses terrestres.
Contrairement à la fusion de l’hydrogène, la fusion du deutérium ne joue aucun rôle quant à la nature de l’objet. La limite à 13 Mj entre planète et naine brune est conventionnelle (et également consensuelle)
Une planète est aussi un corps orbitant autour d’une étoile. Il existe des naines brunes/des planètes non liées à une étoile centrale.
La système solaire
Dans sa présentation traditionnelle, notre Système Solaire est composé d’une étoile (le Soleil) de 8 planètes , 4 telluriques (Mercure, Vénus, la Terre, Mars), 2 géantes gazeuses (Jupiter, Saturne), et 2 glacées (Uranus et Neptune) d'un ensemble de patits corps, planètes naines (dont Pluton), astéroïdes, disque de Kuiper, comètes. Les principales caractéristiques de ces planètes sont regroupées dans le tableau ci-dessous.
Les planètes du système solaire
| Planète | diamètre équatorial (km et en diamètre terrestre) | Masse (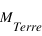 ) ) | Distance (U.A.) | Période (ans) |
| Mercure | 4850 (0.38) | 0.0554 | 0.3871 | 0.2409 |
| Vénus
| 12140 (0.95) | 0.815 | 0.7233 | 0.6152 |
| Terre
| 12756 (1.0) | 1.00 | 1.000 | 1.000 |
| Mars
| 6790 (0.532) | 0.1075 | 1.5237 | 1.8809 |
| Jupiter
| 142600 (11.18) | 317.83 | 5.2028 | 11.8623 |
| Saturne
| 120200 (9.42) | 95.147 | 9.5388 | 29.4577 |
| Uranus
| 49000 (3.84) | 14.54 | 19.1819 | 84.0139 |
| Neptune | 50200 (3.93) | 17.23 | 30.0578 | 164.793 |
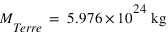
- U.A : distance moyenne Terre-Soleil =
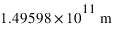
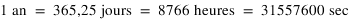
Pluton appartenait à la liste des planètes jusqu'à 2006. Plusieurs objets de même nature que Pluton ont été détectés au delà de l’orbite de Neptune. Ces objets, "trans-neptuniens'", forment le disque de Kuiper. Ils sont des exemples de planétésimaux, les briques à partir desquelles toutes les planètes se sont formées.
Du tableau ci-dessus, il est intéressant d’avoir en tête, pour comparer les caractéristiques des exo-systèmes :
- la masse de Jupiter qui est l’unité de masse pour les planètes géantes,
- la masse de la Terre, unité de masse pour les planètes telluriques,
- l’unité astronomique qui permet d’avoir une idée de la distance de la planète à son étoile, et donc d’évaluer ses principales caractéristiques physiques,
- une idée de la relation distance/période orbitale. Ce dernier point est fondamental pour évaluer les durées d’observations nécessaires à la reconstitution de l’orbite
Loi de Planck -Emission du corps noir-Loi de Stefan-Boltzmann
Par définition, un corps noir est un corps physique idéal, isolé, constitué d’un milieu en équilibre thermodynamique, caractérisé par une température d’équilibre unique. C’est un absorbant parfait et un émetteur idéal. Le champ de rayonnement du corps noir est isotrope, et ne dépend que de la température. La distribution spectrale de l’intensité du rayonnement est donnée par la fonction de Planck qui donne la brillance monochromatique à la fréquence ν du corps noir en fonction de sa température T:
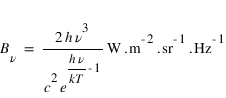
avec
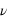 : fréquence en Hz
: fréquence en Hz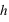 : constante de Planck =
: constante de Planck =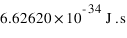
- c : vitesse de la lumière =
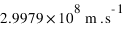
- k : constante de Boltzmann=
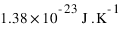
En intégrant la fonction de Planck à toutes les fréquences et sur toutes les directions, on peut déterminer la puissance totale (ou flux) émise par un corps noir à la température T. Cette relation est connue sous le nom de loi de Stefan-Boltzmann :
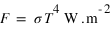
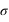 : constante de Stefan =
: constante de Stefan = 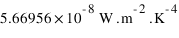
Réciproquement, à toute source émettant un flux F (mesuré par un bolomètre par exemple), on peut associer une température dite « température effective » 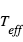 obtenue à partir de F par la loi de Stefan.
obtenue à partir de F par la loi de Stefan.
Température d'équilibre d'une planète
Diagramme Hertzsprung-Russel
Le diagramme de Hertzsprung-Russel (appélé par la suite diagramme HR) tient son nom de l’astronome danois E. Hertzsprung qui l’établit en 1911 et de l’astronome américain H.N Russel qui le redécouvrit indépendamment en 1913. Ce diagramme représente la luminosité absolue d’une étoile (c’est-à-dire indépendante de sa distance à la Terre) en fonction de sa température effective ou toute autre quantité qui lui est reliée (par exemple la différence de luminosité de l’objet vu à travers deux filtres colorés de couleurs (donc de bandes passantes) différentes). Ce diagramme est représenté sur la Figure . La particularité de ce diagramme est d’être à la fois un outil de visualisation de la diversité morphologique des étoiles, mais également de leur évolution au cours du temps. En effet, les étoiles occupent une position qui évolue sur le diagramme HR, de leur naissance, à leur mort.
90 % des étoiles que nous voyons sont à un stade de leur vie que l’on peut qualifier d’« adulte » et occupent une partie du diagramme HR que l’on appelle la « séquence principale » (partie encerclée sur la Figure ). C’est le cas de notre Soleil, qui est né il y a environ 5 milliards d’années, et devrait mourir d’ici 5 milliards d’années également. La particularité des étoiles de la séquence principale est qu’il existe une relation univoque entre leur température effective, leur luminosité absolue, leur masse et leur durée de vie. Comme température effective et couleur sont directement liées par la loi de Stefan, on voit donc que le diagramme HR est un outil très puissant puisqu’il permet à partir de la couleur de l’objet d’en déduire les autres caractéristiques. Par exemple, la durée moyenne de vie « tvie» d’une étoile dépend de sa luminosité ou de sa masse par la relation :
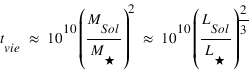
où 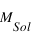 ,
, 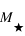 ,
, 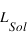 ,
, 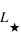 sont respectivement les masses et luminosités absolues de notre Soleil et de l’étoile.
sont respectivement les masses et luminosités absolues de notre Soleil et de l’étoile.
Le diagramme HR permet d’illustrer la notion de classification spectrale, qui consiste à distinguer les étoiles à partir de critères spectroscopiques. La classification spectrale la plus connue et la plus utilisée est celle dite « de Harvard », qui date de 1872. Cette classification, basée sur le seul critère de température des étoiles, les répartit en 9 catégories, dont les 7 premières (O, B, A, F, G, K, M) regroupent environ 99% des étoiles du ciel. Le Tableau ci-dessous décrit les différentes catégories de la classification de Harvard. Cette classification est maintenant étendue aux objet plus froids (étoiles de très faibles masses jusqu’aux objets substellaires) avec l’introduction des type L et T.
Chaque classe est divisée en 10 sous-classes, numérotées de 0 à 9, des étoiles les plus chaudes aux étoiles les plus froides (une étoile G0 est plus chaude qu’une étoile G9).
Les mêmes classes spectrales sont utilisées pour décrire toutes les étoiles quel que soit leur type. Cependant, pour différencier les objets (la température effective d’une géante G0 n’est pas la même que celle d’une étoile de la même classe spectrale G0, mais de la séquence principale), on fait suivre le type spectral d’un numéro, en chiffres romains qui décrit la nature de l’objet avec la convention suivante :
- I : supergéantes
- II : géantes lumineuses
- III : géantes
- IV : sous-géantes
- V : naines
- VI : sous-naines
- VII : naines blanches
Les différentes catégories précédentes correspondent aux différents groupes d’étoiles facilement identifiables sur le diagramme HR
Le Soleil, dans cette classification, est une étoile G2V avec 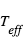 = 5777 K.
= 5777 K.
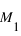 et
et 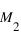 séparées d’une distance R exercent l’une sur l’autre une force attractive parallèle au rayon vecteur qui joint leurs centres de masse respectifs. Cette force s’exprime par la relation :
séparées d’une distance R exercent l’une sur l’autre une force attractive parallèle au rayon vecteur qui joint leurs centres de masse respectifs. Cette force s’exprime par la relation :
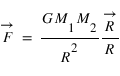
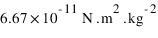
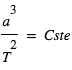
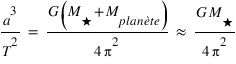
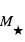 et
et 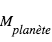 sont respectivement les masses de l’étoile et de la planète.
sont respectivement les masses de l’étoile et de la planète.
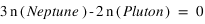
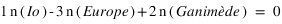
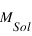 ). On distingue alors, par masse décroissante, 3 catégories d’objets :
). On distingue alors, par masse décroissante, 3 catégories d’objets :
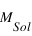 (∼80
(∼80 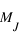 où
où 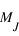 est la masse de Jupiter) la masse est suffisante pour que la contraction gravitationnelle permette d’atteindre au cœur de l’objet la température d’amorçage de la réaction de fusion de l’hydrogène. L’objet est alors appelé « étoile » et son rayon est proportionnel à sa masse
est la masse de Jupiter) la masse est suffisante pour que la contraction gravitationnelle permette d’atteindre au cœur de l’objet la température d’amorçage de la réaction de fusion de l’hydrogène. L’objet est alors appelé « étoile » et son rayon est proportionnel à sa masse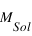 < M < 0.08
< M < 0.08 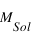 (13
(13 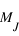 < M < 80
< M < 80 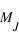 ), la température au cœur de l’objet ne permet pas l’amorçage de la réaction de fusion de l’hydrogène, mais permet l’amorçage de la réaction de fusion du deutérium. L’objet est appelé « naine brune » et son rayon est inversement proportionnel à la racine cubique de sa masse.
), la température au cœur de l’objet ne permet pas l’amorçage de la réaction de fusion de l’hydrogène, mais permet l’amorçage de la réaction de fusion du deutérium. L’objet est appelé « naine brune » et son rayon est inversement proportionnel à la racine cubique de sa masse.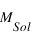 (M < 13
(M < 13 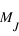 ) la température au cœur de l’objet ne permet pas l’amorçage des réactions de fusion nucléaire. L’objet est appelé « planète ». Au sein de cette catégorie, on distingue généralement les planètes géantes gazeuses des planètes telluriques pour lesquelles la masse n’est pas suffisante pour accréter du gaz. La limite entre planète géante et planète tellurique se situe à environ quelques masses terrestres.
) la température au cœur de l’objet ne permet pas l’amorçage des réactions de fusion nucléaire. L’objet est appelé « planète ». Au sein de cette catégorie, on distingue généralement les planètes géantes gazeuses des planètes telluriques pour lesquelles la masse n’est pas suffisante pour accréter du gaz. La limite entre planète géante et planète tellurique se situe à environ quelques masses terrestres.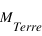 )
)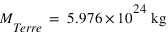
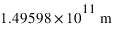
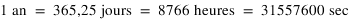
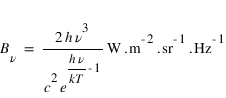
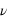 : fréquence en Hz
: fréquence en Hz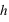 : constante de Planck =
: constante de Planck =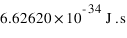
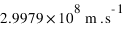
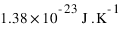
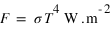
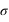 : constante de Stefan =
: constante de Stefan = 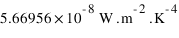
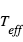 obtenue à partir de F par la loi de Stefan.
obtenue à partir de F par la loi de Stefan.
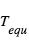 d’une planète en équilibre radiatif, de rayon
d’une planète en équilibre radiatif, de rayon 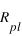 , d’albedo moyen (coefficient de réflexion) A située à une distance D d’une étoile de température
, d’albedo moyen (coefficient de réflexion) A située à une distance D d’une étoile de température 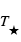 et de rayon
et de rayon 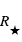 et qui émet un flux
et qui émet un flux 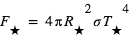 . L’égalité entre le flux stellaire absorbé par la planète
. L’égalité entre le flux stellaire absorbé par la planète 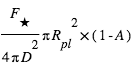 et le flux
et le flux 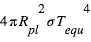 émis par la planète à la température
émis par la planète à la température 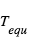 , aboutit à :
, aboutit à :
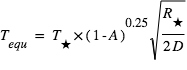
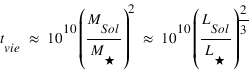
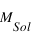 ,
, 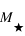 ,
, 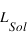 ,
, 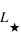 sont respectivement les masses et luminosités absolues de notre Soleil et de l’étoile.
sont respectivement les masses et luminosités absolues de notre Soleil et de l’étoile.
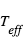 = 5777 K.
= 5777 K.