Température d'équilibre d'une planète

Une application directe de la loi de Stefan est le calcul de la température 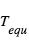d’une planète en équilibre radiatif, de rayon 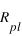, d’albedo moyen (coefficient de réflexion) A située à une distance D d’une étoile de température 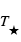et de rayon 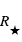et qui émet un flux 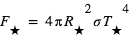. L’égalité entre le flux stellaire absorbé par la planète 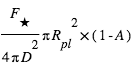et le flux 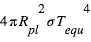émis par la planète à la température 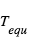, aboutit à :

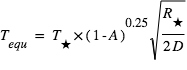
La température d’équilibre de la planète ne dépend pas de la taille de la planète, mais des propriétés de l’étoile, de la distance de la planète et de l'albédo de la planète. Pour les exoplanètes, on peut avoir accès aux propriétés de l'étoile et à la distance étoile-planète. En faisant une hypothèse sur la valeur de l'albédo de la planète, cette formule permet d'estimer la température d'équilibre de la planète.

Les modèles théoriques montrent que la température de l'atmosphère d'une planète peut dépendre d'une manière critique d'autres facteurs que son albédo. Par exemple, la composition de l'atmosphère peut induire des instabilités (emballement de l'effet de serre, par exemple).