Diagramme Hertzsprung-Russel

Le diagramme de Hertzsprung-Russel (appélé par la suite diagramme HR) tient son nom de l’astronome danois E. Hertzsprung qui l’établit en 1911 et de l’astronome américain H.N Russel qui le redécouvrit indépendamment en 1913. Ce diagramme représente la luminosité absolue d’une étoile (c’est-à-dire indépendante de sa distance à la Terre) en fonction de sa température effective ou toute autre quantité qui lui est reliée (par exemple la différence de luminosité de l’objet vu à travers deux filtres colorés de couleurs (donc de bandes passantes) différentes). Ce diagramme est représenté sur la Figure . La particularité de ce diagramme est d’être à la fois un outil de visualisation de la diversité morphologique des étoiles, mais également de leur évolution au cours du temps. En effet, les étoiles occupent une position qui évolue sur le diagramme HR, de leur naissance, à leur mort.

90 % des étoiles que nous voyons sont à un stade de leur vie que l’on peut qualifier d’« adulte » et occupent une partie du diagramme HR que l’on appelle la « séquence principale » (partie encerclée sur la Figure ). C’est le cas de notre Soleil, qui est né il y a environ 5 milliards d’années, et devrait mourir d’ici 5 milliards d’années également. La particularité des étoiles de la séquence principale est qu’il existe une relation univoque entre leur température effective, leur luminosité absolue, leur masse et leur durée de vie. Comme température effective et couleur sont directement liées par la loi de Stefan, on voit donc que le diagramme HR est un outil très puissant puisqu’il permet à partir de la couleur de l’objet d’en déduire les autres caractéristiques. Par exemple, la durée moyenne de vie « tvie» d’une étoile dépend de sa luminosité ou de sa masse par la relation :

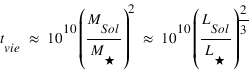
où 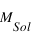, , 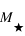, 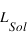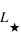sont respectivement les masses et luminosités absolues de notre Soleil et de l’étoile.

Le diagramme HR permet d’illustrer la notion de classification spectrale, qui consiste à distinguer les étoiles à partir de critères spectroscopiques. La classification spectrale la plus connue et la plus utilisée est celle dite « de Harvard », qui date de 1872. Cette classification, basée sur le seul critère de température des étoiles, les répartit en 9 catégories, dont les 7 premières (O, B, A, F, G, K, M) regroupent environ 99% des étoiles du ciel. Le Tableau ci-dessous décrit les différentes catégories de la classification de Harvard. Cette classification est maintenant étendue aux objet plus froids (étoiles de très faibles masses jusqu’aux objets substellaires) avec l’introduction des type L et T.

Chaque classe est divisée en 10 sous-classes, numérotées de 0 à 9, des étoiles les plus chaudes aux étoiles les plus froides (une étoile G0 est plus chaude qu’une étoile G9). Les mêmes classes spectrales sont utilisées pour décrire toutes les étoiles quel que soit leur type. Cependant, pour différencier les objets (la température effective d’une géante G0 n’est pas la même que celle d’une étoile de la même classe spectrale G0, mais de la séquence principale), on fait suivre le type spectral d’un numéro, en chiffres romains qui décrit la nature de l’objet avec la convention suivante :

• I : supergéantes
• II : géantes lumineuses
• III : géantes
• IV : sous-géantes
• V : naines
• VI : sous-naines
• VII : naines blanches

Les différentes catégories précédentes correspondent aux différents groupes d’étoiles facilement identifiables sur le diagramme HR Le Soleil, dans cette classification, est une étoile G2V avec 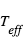= 5777 K.