Gravitation et lois de Kepler

Les lois de Kepler (1571-1630) ont été établies empiriquement à partir des observations détaillées du mouvement de Venus, Mars, Jupiter et Saturne par Tycho Brahe (1546-1601). Les 2 premières lois ont été publiées en 1609 dans Astronomia Nova, la troisième a été publiée en 1619 dans Harmonices Mundi. Elles ne furent démontrées mathématiquement que par la suite, par Isaac Newton (1642-1727)

Les 3 lois de Kepler, bien qu’antérieures à la théorie de Newton, résultent de la loi de la gravitation universelle qui postule que 2 masses 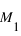et 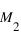séparées d’une distance R exercent l’une sur l’autre une force attractive parallèle au rayon vecteur qui joint leurs centres de masse respectifs. Cette force s’exprime par la relation :

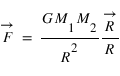
avec G constante universelle de la gravitation =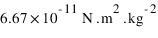

Les lois de Kepler sont toujours vraies pour un système à 2 corps mais restent valables pour des systèmes multiples (plusieurs planètes) dans l’approximation de faible masse des planètes par rapport à l’étoile centrale. Elles ont été énoncées pour le Système Solaire, mais peuvent donc être généralisées à tout système planétaire dont les planètes ont une masse petite devant celle de l'étoile. Mais attention, ce n'est pas le cas de tous les systèmes exoplanétaires!

1. La première loi, dite loi des orbites, (1605), stipule que dans le référentiel héliocentrique, l’orbite de chaque planète est une ellipse dont l’un des foyers est occupé par le Soleil.

2. La seconde loi, dite loi des aires (1604), stipule que le mouvement de chaque planète est tel que le segment de droite reliant le Soleil et la planète balaie des aires égales pendant des durées égales.

3. La troisième loi, dite loi des périodes (1618) stipule que pour toutes les planètes du système, le rapport entre le cube du demi grand axe a de la trajectoire et le carré de la période orbitale T est constant, c'est à dire a la même valeur pour toutes les planètes du système :

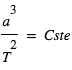
Si a est exprimé en unités astronomiques et T en années terrestres, la constante vaut 1 dans le système solaire.

La loi de la gravitation ci-dessus permet de calculer la valeur de cette constante et de voir que les équations de Kepler font l'approximation que la masse des planètes est négligeable devant la masse de l'étoile:

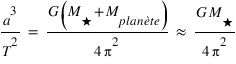
où 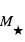et 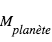sont respectivement les masses de l’étoile et de la planète.