Interfaces entre deux milieux

Auteur: Loïc Rossi

À l'interface entre deux milieux

Illustration d'une interface entre deux milieux d'indices de réfraction n_1

respectivement. Un rayon arrive avec un angle theta_i

à l'interface. Il est en partie réfléchi avec un angle theta_i

et en partie réfracté avec un angle theta_r

Crédit : Loïc Rossi CC-BY-SA

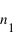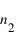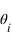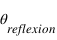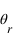Supposons une interface entre deux milieux d'indices respectifs n_1 et n_2 . Un rayon arrive sur cette interface avec un angle theta_i par rapport à la normale à l'interface. Une partie est réfléchie avec un angle theta_reflexion et une partie est réfractée avec un angle theta_r .

Les lois de Snell-Descartes

Dans le cadre de l'optique géométrique, les lois de Snell-Descartes énoncent que :

Le rayon réfléchi et le rayon réfracté sont dans le plan d'incidence ;
L'angle de réflexion est égal à l'angle d'incidence :
On a, entre l'angle de réfraction et l'angle d'incidence,

Du point de vue des ondes électromagnétiques

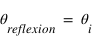
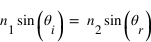
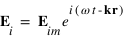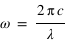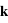Une onde électromagnétique incidente peut être décrite sous la forme suivante : vecteur(E_i) = vecteur(E_im) * exp(i*(omega*t-vecteur(k)*vecteur(r))) où omega = 2*pi*c/lambda , et où et 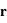sont le vecteur d'onde et le vecteur position respectivement. 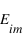E_im est le module du vecteur de champ électrique incident.

Par la suite on notera avec 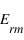E_rm le module du champ électrique réfléchi par l'interface et 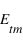E_tm le module du champ transmis par l'interface. On va définir deux coefficients : le coefficient de transmission 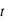et le coefficient de réflexion 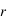, tels que :

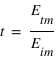
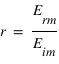
Pour déterminer l'expression 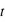de et de 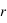on va s'intéresser à deux cas de polarisation de l'onde incidente.