| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
|
Si on suppose maintenant que la polarisation du champ 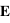 est dans le plan d'incidence, on aura :
est dans le plan d'incidence, on aura : 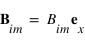 .
.
Pour le champ magnétique, on a la relation de continuité 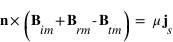 liant les composantes tangentielles du champ avec le courant surfacique parcourant l'interface. Ici, ce courant est nul, ce qui nous permet d'écrire que :
liant les composantes tangentielles du champ avec le courant surfacique parcourant l'interface. Ici, ce courant est nul, ce qui nous permet d'écrire que :
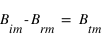 (1)
(1)
ainsi que 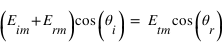 (2)
(2)
En utilisant à nouveau la relation 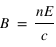 , on peut écrire :
, on peut écrire :
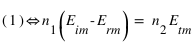 ,
, 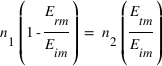
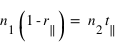 (3)
(3)L'équation (2) devient quant à elle, avec la même astuce :
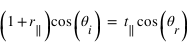 (4)
(4)
En utilisant les expressions (3) et (4) on retrouve les deux autres coefficients de Fresnel :
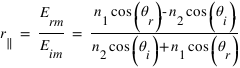
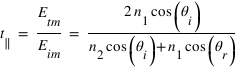
Les coefficients de Fresnel mettent à jour un cas particulier. En effet si 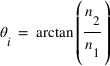 , on a
, on a 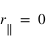 ! L'onde polarisée parallèlement au plan d'incidence (perpendiculairement à l'interface) est totalement transmise ! Cet angle particulier porte le nom d'angle de Brewster d'après David Brewster qui l'a mis en évidence le premier.
! L'onde polarisée parallèlement au plan d'incidence (perpendiculairement à l'interface) est totalement transmise ! Cet angle particulier porte le nom d'angle de Brewster d'après David Brewster qui l'a mis en évidence le premier.