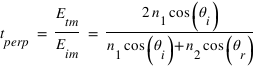| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
|
Si on suppose que l'onde incidente est polarisée perpendiculairement au plan d'incidence, on a : 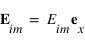 .
.
À l'interface entre les deux milieux, et à partir des lois de Maxwell, on a des relations de continuité entre les différentes composantes des champs électrique et magnétique. Ainsi, les composantes tangentielles du champ électrique se conservent. Les champs électriques étant déjà parallèles à l'interface, on a donc : 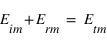 (1).
(1).
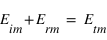 (1)
(1)
En ce qui concerne le champ magnétique, ce sont les composantes normales qui sont conservées. Comme 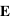 est perpendiculaire à
est perpendiculaire à 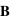 , les champs magnétiques incidents, transmis et réfléchis sont dans le plan d'incidence et on a, par projection sur l'axe (Oz) :
, les champs magnétiques incidents, transmis et réfléchis sont dans le plan d'incidence et on a, par projection sur l'axe (Oz) :
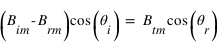 (2) où
(2) où 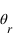 est l'angle de réfraction.
est l'angle de réfraction.
Par ailleurs, l'équation de Maxwell-Faraday permet d'établir que 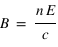 . On peut alors écrire :
. On peut alors écrire :
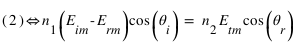 .
.
En remplaçant 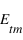 par son expression en (1), on peut écrire :
par son expression en (1), on peut écrire : 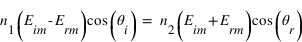 . Ce qui devient, après quelques arrangements :
. Ce qui devient, après quelques arrangements :
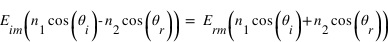
et donne finalement les coefficients de réflexion et de transmission, dits coefficients de Fresnel :