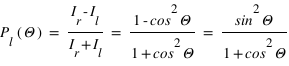Supposons une interface entre deux milieux d'indices respectifs 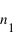 et
et 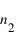 . Un rayon arrive sur cette interface avec un angle
. Un rayon arrive sur cette interface avec un angle 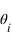 par rapport à la normale à l'interface. Une partie est réfléchie avec un angle
par rapport à la normale à l'interface. Une partie est réfléchie avec un angle 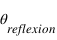 et une partie est réfractée avec un angle
et une partie est réfractée avec un angle 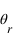 .
.
À l'interface entre deux milieux
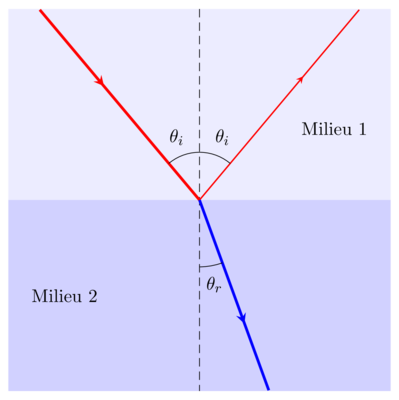
Illustration d'une interface entre deux milieux d'indices de réfraction
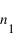
et
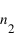
respectivement. Un rayon arrive avec un angle
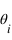
à l'interface. Il est en partie réfléchi avec un angle
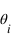
et en partie réfracté avec un angle
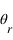
.
Crédit :
Loïc Rossi CC-BY-SA
Si on suppose que l'onde incidente est polarisée perpendiculairement au plan d'incidence, on a : 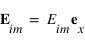 .
.
Cas où E est perpendiculaire
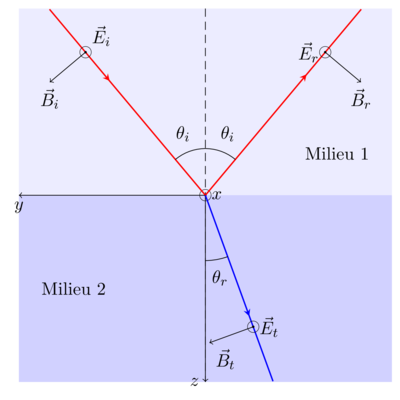
Un rayon incident arrive avec un angle
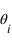
avec la normale à une interface. Le rayon incident est polarisé perpendiculairement au plan d'incidence.
Crédit :
Loïc Rossi CC-BY-SA
À l'interface entre les deux milieux, et à partir des lois de Maxwell, on a des relations de continuité entre les différentes composantes des champs électrique et magnétique. Ainsi, les composantes tangentielles du champ électrique se conservent. Les champs électriques étant déjà parallèles à l'interface, on a donc : 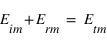 (1).
(1).
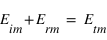 (1)
(1)
En ce qui concerne le champ magnétique, ce sont les composantes normales qui sont conservées. Comme 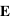 est perpendiculaire à
est perpendiculaire à 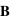 , les champs magnétiques incidents, transmis et réfléchis sont dans le plan d'incidence et on a, par projection sur l'axe (Oz) :
, les champs magnétiques incidents, transmis et réfléchis sont dans le plan d'incidence et on a, par projection sur l'axe (Oz) :
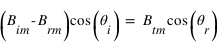 (2) où
(2) où 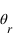 est l'angle de réfraction.
est l'angle de réfraction.
Par ailleurs, l'équation de Maxwell-Faraday permet d'établir que 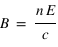 . On peut alors écrire :
. On peut alors écrire :
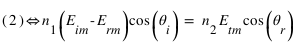 .
.
En remplaçant 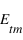 par son expression en (1), on peut écrire :
par son expression en (1), on peut écrire : 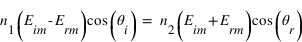 . Ce qui devient, après quelques arrangements :
. Ce qui devient, après quelques arrangements :
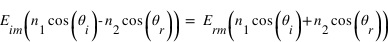
et donne finalement les coefficients de réflexion et de transmission, dits coefficients de Fresnel :
Si on suppose maintenant que la polarisation du champ 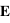 est dans le plan d'incidence, on aura :
est dans le plan d'incidence, on aura : 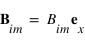 .
.
Cas où E est parallèle
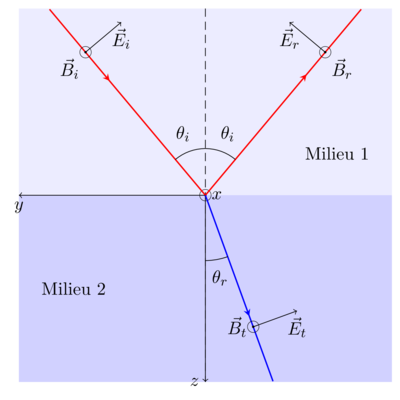
Un rayon incident arrive avec un angle
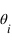
avec la normale à une interface. Le rayon incident est polarisé parallèlement au plan d'incidence.
Crédit :
Loïc Rossi CC-BY-SA
Pour le champ magnétique, on a la relation de continuité 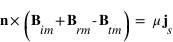 liant les composantes tangentielles du champ avec le courant surfacique parcourant l'interface. Ici, ce courant est nul, ce qui nous permet d'écrire que :
liant les composantes tangentielles du champ avec le courant surfacique parcourant l'interface. Ici, ce courant est nul, ce qui nous permet d'écrire que :
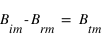 (1)
(1)
ainsi que 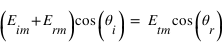 (2)
(2)
En utilisant à nouveau la relation 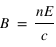 , on peut écrire :
, on peut écrire :
L'équation (2) devient quant à elle, avec la même astuce :
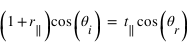 (4)
(4)
En utilisant les expressions (3) et (4) on retrouve les deux autres coefficients de Fresnel :
Les coefficients de Fresnel mettent à jour un cas particulier. En effet si 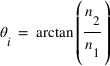 , on a
, on a 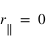 ! L'onde polarisée parallèlement au plan d'incidence (perpendiculairement à l'interface) est totalement transmise ! Cet angle particulier porte le nom d'angle de Brewster d'après David Brewster qui l'a mis en évidence le premier.
! L'onde polarisée parallèlement au plan d'incidence (perpendiculairement à l'interface) est totalement transmise ! Cet angle particulier porte le nom d'angle de Brewster d'après David Brewster qui l'a mis en évidence le premier.
 Coefficients de réflexion et transmission
Coefficients de réflexion et transmission
Les coefficients calculés ci-avant sont des coefficients de réflexion et de transmission en amplitude des ondes. Or on mesure généralement l'intensité de la lumière. On va donc utiliser des considérations énergétiques (conservation de l'énergie notamment) pour définir les coefficients de réflexion et transmission à l'interface.
Les deux cas étudiés précédements sont applicables au cas général où la lumière n'est pas polarisée. En effet, on peut considérer la lumière naturelle comme ayant une composante polarisée parallèlement au plan d'incidence et une composante polarisée perpendiculairement au plan d'incidence.
C'est l'étude de la lumière transmise ou réfléchie par un corps dans différentes polarisations qui va fournir des informations sur le milieu, car les coefficients de Fresnel dépendent de la géométrie, mais aussi des caractéristiques des milieux, via 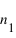 et
et 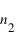 .
.
Emissivité
On peut s'intéresser à la polarisation du rayonnement thermique issu d'un corps. Normalement le rayonnement thermique n'est pas polarisé, mais la traversée du milieu (le sol par exemple) va le polariser et l'on va pouvoir mesurer cet effet. C'est ce qui est utilisé par exemple par la sonde Cassini qui étudie Titan.
On va donc s'intéresser à la transmission du corps en fonction de la géométrie d'observation et de son indice de réfraction (ou sa permittivité électrique). On parlera alors d'emissivité du corps.
v
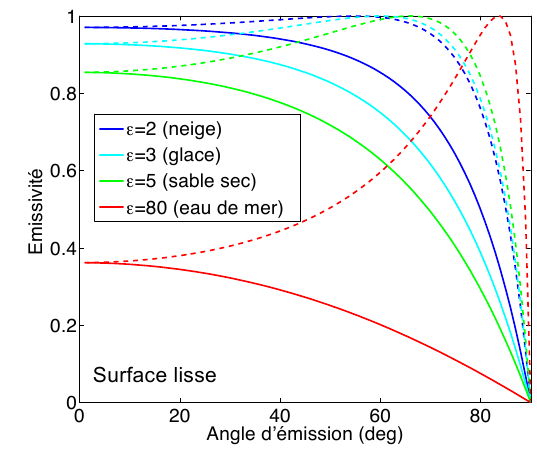
Figure montrant l'emissivité en fonction de l'angle d'émission pour différentes permittivités. Les courbes pleines correspondent à la polarisation perpendiculaire et les courbes en tirets correspondent à la polarisation parallèle. On voit ainsi que l'emissivité diminue avec la hausse de la permittivité.
Crédit :
Figure produite par Alice Le Gall (LATMOS)
Carte d'emissivité du pole nord de Titan
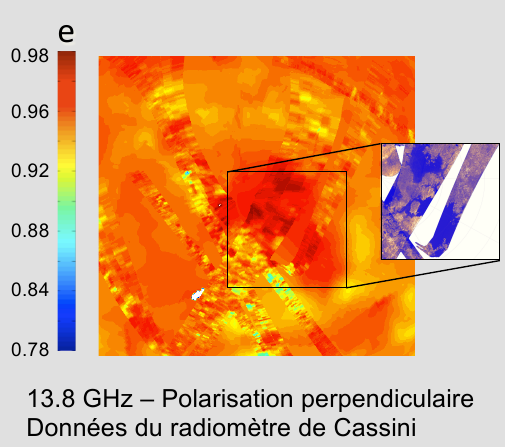
Carte d'émissivité du pôle de Titan obtenue par le radiomètre de Cassini en polarisation perpendiculaire. L'emissivité mesurée a permis d'établir que la permitivité des lacs de Titan est entre 1,6 et 1,9 : ce sont des lacs d'hydrocarbures !
On mesure généralement le degré de polarisation 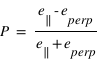 où
où 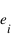 est l'émissivité en polarisation parallèle ou perpendiculaire au plan de diffusion.
est l'émissivité en polarisation parallèle ou perpendiculaire au plan de diffusion.
Reflexion
On peut également utiliser cette méthode de façon active en envoyant une onde polarisée sur une surface avec un radar et en étudiant la réflexion de cette onde sur le corps étudié. (Donner Exemple)
La diffusion Rayleigh se produit dans le cas de diffuseurs petits par rapport à la longueur (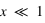 ), ayant un indice de réfraction proche de l'unité ou satisfaisant
), ayant un indice de réfraction proche de l'unité ou satisfaisant 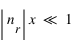 .
.
La diffusion Rayleigh
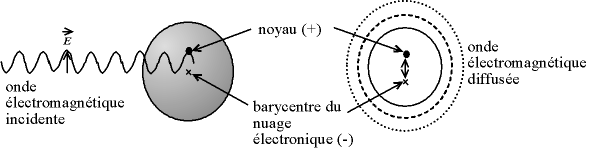
Une onde électromagnétique incidente fait osciller le nuage électroniques des atomes. Le dipôle électrostatique généré rayonne une onde électromagnétique de même longueur d'onde : la diffusion Rayleigh.
Crédit :
Christophe Dang Ngoc Chan, CC-BY-SA
Lorsqu'un onde électromagnétique rencontre le diffuseur, elle génère un dipôle électrostatique de moment 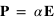 , où
, où 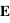 est le champ électrique incident et α la polarisabilité du diffusant. Ce dipôle va rayonner une onde de même fréquence dans toutes les directions. Cependant, l'intensité et la polarisation de l'onde rayonnée vont dépendre de l'angle de diffusion.
est le champ électrique incident et α la polarisabilité du diffusant. Ce dipôle va rayonner une onde de même fréquence dans toutes les directions. Cependant, l'intensité et la polarisation de l'onde rayonnée vont dépendre de l'angle de diffusion.
On peut montrer que la fonction de phase est 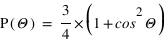 , où Θ est l'angle de diffusion.
, où Θ est l'angle de diffusion.
En ce qui concerne la polarisation, on va considérer que la lumière incidente est non polarisée (ce qui est vrai pour la lumière solaire) et considérer les directions parallèle et perpendiculaire au plan de diffusion, que l'on va noter avec les indices 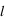 et
et 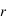 respectivement. La composante diffusée polarisée perpendiculairement au plan de diffusion,
respectivement. La composante diffusée polarisée perpendiculairement au plan de diffusion, 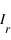 ne dépend pas de Θ, tandis que
ne dépend pas de Θ, tandis que 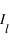 évolue en
évolue en 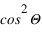 . Dès lors, si on s'intéresse au degré linéaire de polarisation, on aura :
. Dès lors, si on s'intéresse au degré linéaire de polarisation, on aura :
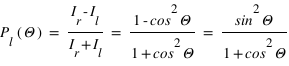
Ceci rend compte du maximum de polarisation observé par diffusion Rayleigh pour un angle de phase de 90°.
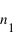 et
et 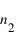 . Un rayon arrive sur cette interface avec un angle
. Un rayon arrive sur cette interface avec un angle 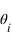 par rapport à la normale à l'interface. Une partie est réfléchie avec un angle
par rapport à la normale à l'interface. Une partie est réfléchie avec un angle 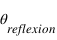 et une partie est réfractée avec un angle
et une partie est réfractée avec un angle 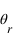 .
.

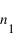 et
et 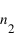 respectivement. Un rayon arrive avec un angle
respectivement. Un rayon arrive avec un angle 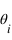 à l'interface. Il est en partie réfléchi avec un angle
à l'interface. Il est en partie réfléchi avec un angle 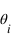 et en partie réfracté avec un angle
et en partie réfracté avec un angle 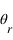 .
.
 Les lois de Snell-Descartes
Les lois de Snell-Descartes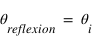
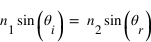
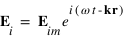 où
où 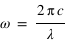 , et où
, et où 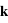 et
et 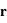 sont le vecteur d'onde et le vecteur position respectivement.
sont le vecteur d'onde et le vecteur position respectivement. 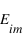 est le module du vecteur de champ électrique incident.
est le module du vecteur de champ électrique incident.
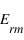 le module du champ électrique réfléchi par l'interface et
le module du champ électrique réfléchi par l'interface et 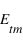 le module du champ transmis par l'interface. On va définir deux coefficients : le coefficient de transmission
le module du champ transmis par l'interface. On va définir deux coefficients : le coefficient de transmission 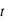 et le coefficient de réflexion
et le coefficient de réflexion 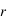 , tels que :
, tels que :
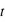 et de
et de 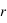 on va s'intéresser à deux cas de polarisation de l'onde incidente.
on va s'intéresser à deux cas de polarisation de l'onde incidente.
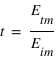
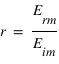
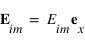 .
.

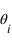 avec la normale à une interface. Le rayon incident est polarisé perpendiculairement au plan d'incidence.
avec la normale à une interface. Le rayon incident est polarisé perpendiculairement au plan d'incidence.
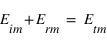 (1).
(1).
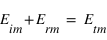 (1)
(1)
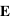 est perpendiculaire à
est perpendiculaire à 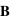 , les champs magnétiques incidents, transmis et réfléchis sont dans le plan d'incidence et on a, par projection sur l'axe (Oz) :
, les champs magnétiques incidents, transmis et réfléchis sont dans le plan d'incidence et on a, par projection sur l'axe (Oz) :
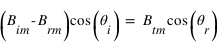 (2) où
(2) où 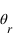 est l'angle de réfraction.
est l'angle de réfraction.
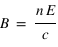 . On peut alors écrire :
. On peut alors écrire :
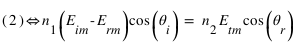 .
.
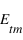 par son expression en (1), on peut écrire :
par son expression en (1), on peut écrire : 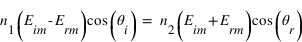 . Ce qui devient, après quelques arrangements :
. Ce qui devient, après quelques arrangements :
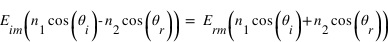
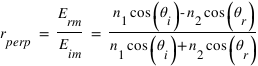
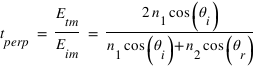
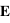 est dans le plan d'incidence, on aura :
est dans le plan d'incidence, on aura : 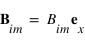 .
.

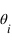 avec la normale à une interface. Le rayon incident est polarisé parallèlement au plan d'incidence.
avec la normale à une interface. Le rayon incident est polarisé parallèlement au plan d'incidence.
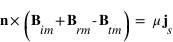 liant les composantes tangentielles du champ avec le courant surfacique parcourant l'interface. Ici, ce courant est nul, ce qui nous permet d'écrire que :
liant les composantes tangentielles du champ avec le courant surfacique parcourant l'interface. Ici, ce courant est nul, ce qui nous permet d'écrire que :
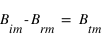 (1)
(1)
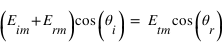 (2)
(2)
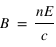 , on peut écrire :
, on peut écrire :
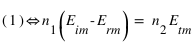 ,
, 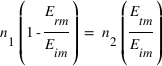
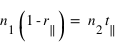 (3)
(3)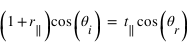 (4)
(4)
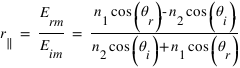
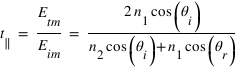
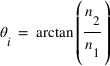 , on a
, on a 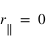 ! L'onde polarisée parallèlement au plan d'incidence (perpendiculairement à l'interface) est totalement transmise ! Cet angle particulier porte le nom d'angle de Brewster d'après David Brewster qui l'a mis en évidence le premier.
! L'onde polarisée parallèlement au plan d'incidence (perpendiculairement à l'interface) est totalement transmise ! Cet angle particulier porte le nom d'angle de Brewster d'après David Brewster qui l'a mis en évidence le premier.
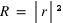
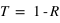
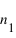 et
et 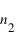 .
.


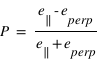 où
où 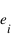 est l'émissivité en polarisation parallèle ou perpendiculaire au plan de diffusion.
est l'émissivité en polarisation parallèle ou perpendiculaire au plan de diffusion.
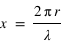 , où
, où 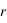 est le rayon du diffusant et
est le rayon du diffusant et 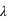 la longueur d'onde du photon incident. Le paramètre de taille permet de distinguer le régime de Rayleigh et celui de Mie :
la longueur d'onde du photon incident. Le paramètre de taille permet de distinguer le régime de Rayleigh et celui de Mie :
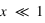 , on est dans le régime de Rayleigh, où les particules sont petites devant la longueur d'onde ;
, on est dans le régime de Rayleigh, où les particules sont petites devant la longueur d'onde ;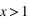 , on est dans le régime de Mie, avec des effets particuliers, notamment d'interférences ;
, on est dans le régime de Mie, avec des effets particuliers, notamment d'interférences ;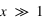 , on rentre dans l'approximation de l'optique géométrique. Certains effets de la diffusion de Mie ne sont plus expliqués simplement par l'optique géométrique.
, on rentre dans l'approximation de l'optique géométrique. Certains effets de la diffusion de Mie ne sont plus expliqués simplement par l'optique géométrique. 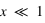 ), ayant un indice de réfraction proche de l'unité ou satisfaisant
), ayant un indice de réfraction proche de l'unité ou satisfaisant 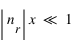 .
.

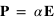 , où
, où 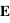 est le champ électrique incident et
est le champ électrique incident et 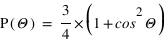 , où
, où 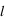 et
et 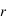 respectivement. La composante diffusée polarisée perpendiculairement au plan de diffusion,
respectivement. La composante diffusée polarisée perpendiculairement au plan de diffusion, 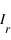 ne dépend pas de
ne dépend pas de 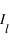 évolue en
évolue en 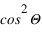 . Dès lors, si on s'intéresse au degré linéaire de polarisation, on aura :
. Dès lors, si on s'intéresse au degré linéaire de polarisation, on aura :