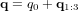L'orientation d'un satellite dans l'espace correspond à l'orientation du repère fixé sur son corps par rapport à un autre repère, tel que ceux vus précédemment. Ainsi, la détermination d'attitude d'un satellite en particulier requiert des méthodes d'estimation de la matrice orthogonale transformant des vecteurs d'un référentiel de référence fixé dans l'espace à un référentiel fixé par rapport au corps du satellite. De plus, une mission spatiale ne peut être définie par un unique référentiel. En fonction des besoins, de l'échelle à laquelle on se place, il est nécessaire d'utiliser tel ou tel référentiel. Dès lors, le passage d'un référentiel à un autre devient un aspect crucial du SCAO. L'une des plus importantes propriétés des matrices d'attitude est énoncée par le théorème d'Euler.
 Théorème d'Euler
Théorème d'Euler
L'orientation instantanée d'un objet peut toujours être décrite par une unique rotation autour d'un axe fixe.
On peut parler de pôle eulérien pour nommer le centre de rotation. Il doit son nom au mathématicien et physicien suisse Leonhard Euler. Dès lors qu'un point d'un solide reste fixe lors d'un déplacement, ce déplacement est équivalent à une rotation autour d'un axe passant par le point fixe (pôle eulérien). En algèbre linéaire, ce théorème implique que deux référentiels cartésiens partageant la même origine sont reliés par une rotation autour d'un axe fixe.
Leonhard Euler

Portrait par Johann Georg Brucker (1756).
Crédit :
Domaine public
Les relations permettant de jongler entre les systèmes de coordonnées peuvent être charactérisées de différentes manières, comportant chacune leurs lots d'avantages et inconvénients. Certaines d'entre elles sont présentées dans la partie suivante :
Les démonstrations des principales relations sont proposées en exercices.
La façon la plus évidente de donner l'orientation d'un référentiel par rapport à un autre est d'exprimer leurs vecteurs de base dans l'autre repère.
Propriétés de la MCD
La MCD est une matrice orthogonale, ce qui signifie que son inverse est égal à sa transposée :
![[T]^{-1} = [T]^T](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation32.png) et
et ![[T][T]^T = [I] = [T]^T[T]](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation33.png)
![\bold v_R = [T]_{R|B}^T \bold v_B = \begin{pmatrix} \bold B_x \cdot \bold R_x & \bold B_y \cdot \bold R_x & \bold B_z \cdot \bold R_x \\ \bold B_x \cdot \bold R_y & \bold B_y \cdot \bold R_y & \bold B_z \cdot \bold R_y \\ \bold B_x \cdot \bold R_z & \bold B_y \cdot \bold R_z & \bold B_z \cdot \bold R_z \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation34.png)
Les transformations successives entre référentiels peuvent être déterminées par une série de multiplications matricielles. Par exemple, la transformation du référentiel inertiel au référentiel du satellite peut être décomposée de la manière suivante : transformation du référentiel inertiel au référentiel fixé sur la Terre multipliée par la transformation du référentiel fixé sur la Terre au référentiel orbital, le tout multiplié par la transformation du repère orbital au repère du satellite.
![[T]_{sat|inertiel} = [T]_{sat|orbite} [T]_{orbite|Terre} [T]_{Terre|inertiel}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation35.png)
Limitations de cette représentation
Malgré certains avantages, la MCD n'est pas toujours la représentation la plus adaptée. Elle utilise 9 paramètres pour décrire une orientation, parmi lesquels seulement 3 sont indépendants.
Présentation des angles d'Euler
Les angles d'Euler sont les angles introduits par Leonhard Euler pour décrire l'orientation d'un solide. Ils peuvent être utilisés pour définir l'orientation d'un référentiel par rapport à un autre. On obtient une rotation en faisant varier l'un des trois angles d'Euler et une séquence de 3 rotations est suffisante pour décrire n'importe quelle transformation. La première rotation est effectuée selon n'importe quel axe, tandis que les deux suivantes ne peuvent jamais être effectuées autour d'un axe utilisé par la rotation précédente. Au total, 12 jeux d'angles d'Euler existent : (1,2,1), (1,2,3), (1,3,1), (1,3,2), (2,1,2), (2,1,3), (2,3,1), (2,3,2), (3,1,2), (3,1,3), (3,2,1), (3,2,3). L'ordre des rotations et la valeur des angles ne sont pas uniques et sont sujets à des singularités mathématiques.
Exemples
 Appliquette interactive
Appliquette interactive
Une appliquette interactive est disponible ici. Elle permet de visualiser dans l'espace les séquences d'Euler qui sont introduites dans cette section à titre d'exemple.
- La séquence d'Euler la plus connue, nommée d'après lui, est la séquence (3,1,3). Elle a notamment été utilisée pour étudier le mouvement gyroscopique avec les trois rotations successives :
- La précession
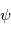 , autour de l'axe Oz, fait passer de (O,x,y,z) au référentiel (O,u,v,z) (en bleu).
, autour de l'axe Oz, fait passer de (O,x,y,z) au référentiel (O,u,v,z) (en bleu). - La nutation
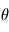 , autour de l'axe Ou (ligne des nœuds), fait passer de (O,u,v,z) à (O,u,w,z’) (en vert).
, autour de l'axe Ou (ligne des nœuds), fait passer de (O,u,v,z) à (O,u,w,z’) (en vert). - La giration
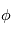 , ou rotation propre, autour de l'axe Oz’, fait passer de (O,u,w,z’) au référentiel lié au solide (O,x’,y’,z’) (en rouge).
, ou rotation propre, autour de l'axe Oz’, fait passer de (O,u,w,z’) au référentiel lié au solide (O,x’,y’,z’) (en rouge).
Cette séquence peut également être utilisée pour décrire les paramètres orbitaux d'un satellite par rapport au référentiel inertiel centré sur la Terre. La première rotation correspond alors à l'angle du noeud ascendant, 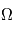 , autour de l'axe
, autour de l'axe  . La deuxième rotation est l'inclinaison,
. La deuxième rotation est l'inclinaison, 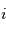 , autour de la ligne de noeuds. La dernière rotation est l'anomalie vraie,
, autour de la ligne de noeuds. La dernière rotation est l'anomalie vraie, 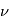 , autour de la normale à l'orbite.
, autour de la normale à l'orbite. - La séquence (3-1-2) est souvent utilisée pour décrire l'orientation d'un satellite par rapport au référentiel orbital.
- La première rotation correspond au lacet, autour du nadir.
- La suivante est le roulis, autour de l'axe
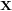 du satellite.
du satellite. - La dernière est le tangage.
Les angles d'Euler décrivent une rotation unique, ce qui est généralement un avantage par rapport à la MCD. Cependant, à une orientation donnée correspondent plusieurs jeux d'angles d'Euler.
Limites de cette représentation
D'une manière générale, les angles d'Euler déterminent une orientation unique, ce qui est un avantage sur la MCD. Des singularités apparaissent lorsque le deuxième angle d'Euler aligne les premier et troisième axes de rotation. Dans ce cas, cette description d'attitude à 3 degrés dégénère en une description à seulement 2 degrés de liberté. Cette condition est réalisée lorsque l'angle vaut 90 et 270 degrés pour les 6 rotations où les premier et troisième axes sont différents, et lorsque l'angle vaut 0 et 190 degrés pour les 6 rotations où les premier et troisième axes sont identiques.
Séquence d'Euler pour les paramètre orbitaux
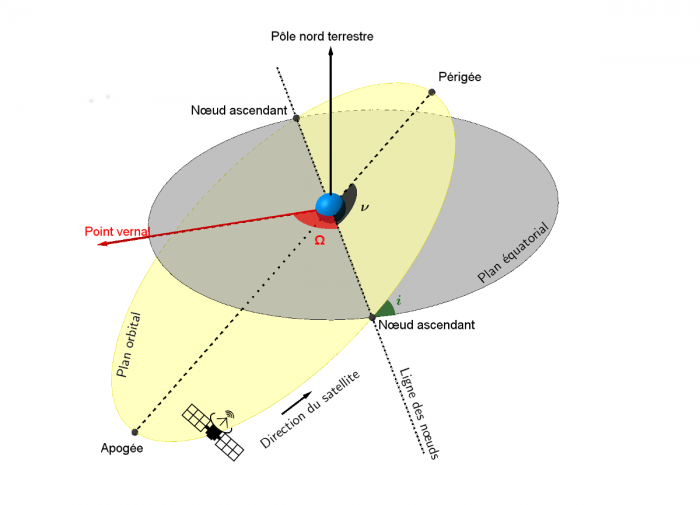
La séquence d'Euler (3-1-3) correspond aux paramètres orbitaux habituellement utilisés pour un satellite en orbite terrestre : le nœud ascendant (
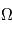
), l'inclinaison (
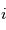
) et l'anomalie vraie (
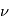
).
Crédit :
Gary Quinsac
Séquence d'Euler pour les roulis, tangage et lacet
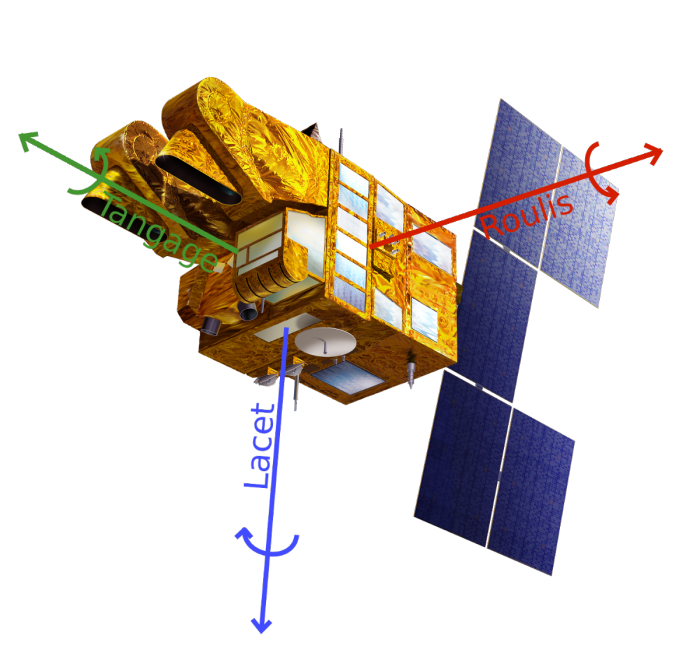
La séquence d'Euler (3-1-2) correspond aux angles de roulis, tangage et lacet. Ils sont illustrés avec le satellite d'observation de la Terre SPOT 3.
Crédit :
Gary Quinsac
Afin de s'affranchir du problème de singularité rencontré avec les angles d'Euler, une représentation de l'attitude composée de 4 éléments est introduite sous le nom de quaternion (dont les éléments sont appelés paramètres d'Euler). Cette construction mathématique est présentée plus en détail dans la partie suivante.
Des quaternions à la MCD
De la même façon que l'on peut exprimer la MCD en fonction des angles d'Euler, elle peut être paramétrée en fonction d'un quaternion de la manière suivante :
![[T]_{B|R} = [T(\bold q)] = \begin{pmatrix} 1-2(q_2^2+q_3^2) & 2(q_1q_2+q_3q_0) & 2(q_1 q_3 - q_2 q_0) \\ 2(q_2q_1-q_3q_0) & 1-2(q_1^2+q_3^2) & 2(q_2q_3+q_1q_0) \\ 2(q_3q_1+q_2q_0) & 2(q_3q_2-q_1q_0) & 1-2(q_1^2+q_2^2) \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude-quaternions/equation15.png)
Propriétés des quaternions
Avantage des quaternions
Un avantage inhérent à cette représentation est que les équations de la cinématique deviennent purement algébriques et ne contiennent plus de fonctions trigonométriques.
Les quaternions sont un système de nombres premièrement décrits par William Rowan Hamilton en 1843 appliqué à la mécanique et à l'espace à 3 dimensions.
 William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton (04/08/1805 - 02/09/1865) est un mathématicien, physicien et astronome irlandais (né et mort à Dublin). Outre sa découverte des quaternions, il contribua également au développement de l'optique, de la dynamique et de l'algèbre. Ses recherches se révélèrent importantes pour le développement de la mécanique quantique.
William Rowan Hamilton
Peinture de Sir William Rowan Hamilton.
Crédit :
Domaine public
Définition mathématique
Un quaternion q est une expression de la forme :
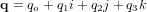
où 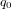 ,
, 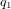 ,
, 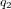 ,
, 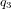 sont des nombres réels, et
sont des nombres réels, et 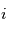 ,
, 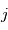 ,
, 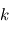 sont des symboles respectant les relations quaternioniques :
sont des symboles respectant les relations quaternioniques :
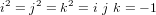
Par analogie avec les nombres complexes, 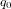 est appelé partie réelle de
est appelé partie réelle de  et
et 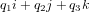 est appelé partie imaginaire.
est appelé partie imaginaire.
L'ensemble des quaternions est un espace vectoriel de dimension 4 et de base 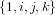 où s'applique l'addition composant par composant. Soient deux quaternions
où s'applique l'addition composant par composant. Soient deux quaternions  et
et  :
:
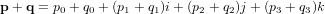
Afin d'introduire la multiplication, il faut d'abord introduire le produit hamiltonien. Les produits des éléments de base 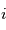 ,
, 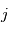 et
et 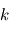 sont définis de la manière suivante :
sont définis de la manière suivante :
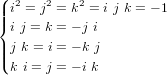
La multiplication de quaternions est associative et distributive, mais pas commutative en général. Pour les quaternions q et p elle est définie par :
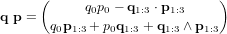
Elle peut être représentée par une multiplication matricielle. Dans ce cas, une matrice composée de valeurs du premier quaternion vient multiplier le second quaternion, tel que : ![\bold q \ \bold p = [Q(\bold q)] \bold p](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude-quaternions/equation53.png)
avec ![[Q(\bold q)] = \begin{pmatrix} q_0 & -q_1 & -q_2 & -q_3 \\ q_1 & q_0 & -q_3 & q_2 \\ q_2 & q_3 & q_0 & -q_1 \\ q_3 & -q_2 & q_1 & q_0 \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude-quaternions/equation54.png) .
.
Le conjugué, la norme et l'inverse des quaternions  et
et  sont :
sont :
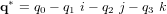 et
et 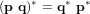
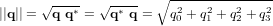 et
et 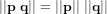
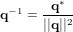
 Théorème d'Euler
Théorème d'Euler
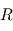 , avec les axes
, avec les axes 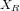 et
et 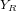 , incliné par rapport à un référentiel
, incliné par rapport à un référentiel 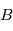 , d'axes
, d'axes 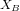 et
et 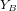 , d'un angle
, d'un angle 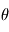 . Le vecteur
. Le vecteur 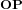 peut être exprimé dans ces deux systèmes sous forme matricielle :
peut être exprimé dans ces deux systèmes sous forme matricielle :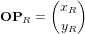 et
et 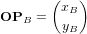 .
.
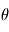 . Cette matrice transforme le vecteur
. Cette matrice transforme le vecteur 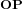 du premier référentiel
du premier référentiel 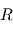 vers le second
vers le second 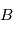 .
.
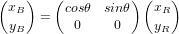
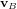 dans
dans 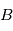 à partir de son expression
à partir de son expression 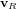 dans
dans 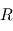 s'écrit :
s'écrit :
![\bold v_B = [T]_{B|R} \bold v_R](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation20.png) avec
avec ![[T]_{B|R} = \begin{pmatrix} \bold B_x \cdot \bold R_x & \bold B_x \cdot \bold R_y & \bold B_x \cdot \bold R_z \\ \bold B_y \cdot \bold R_x & \bold B_y \cdot \bold R_y & \bold B_y \cdot \bold R_z \\ \bold B_z \cdot \bold R_x & \bold B_z \cdot \bold R_y & \bold B_z \cdot \bold R_z \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation21.png)
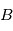 par rapport à
par rapport à 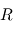 . On l'appelle également matrice de rotation ou matrice de transformation des coordonnées de
. On l'appelle également matrice de rotation ou matrice de transformation des coordonnées de 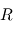 vers
vers 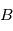 .
.
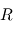 autour de chacun de ses trois axes se retrouvent décrites par les matrices de rotation suivantes :
autour de chacun de ses trois axes se retrouvent décrites par les matrices de rotation suivantes :
![[T(\theta_1)]_1 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & c_{\theta_1} & s_{\theta_1} \\ 0 & -s_{\theta_1} & c_{\theta_1} \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation27.png) ,
, ![[T(\theta_2)]_2 = \begin{pmatrix} c_{\theta_2} & 0 & -s_{\theta_2} \\ 0 & 1 & 0 \\ s_{\theta_2} & 0 & c_{\theta_2} \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation28.png) et
et ![[T(\theta_3)]_3 = \begin{pmatrix} c_{\theta_3} & s_{\theta_3} & 0 \\ -s_{\theta_3} & c_{\theta_3} & 0 \\ 0 & 0 & 1 \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation29.png)
![[T(\theta_i)]_i](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation30.png) indique une rotation d'angle
indique une rotation d'angle 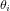 autour du i-ème axe du référentiel fixé sur le corps.
autour du i-ème axe du référentiel fixé sur le corps.
![[T]^{-1} = [T]^T](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation32.png) et
et ![[T][T]^T = [I] = [T]^T[T]](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation33.png)
![\bold v_R = [T]_{R|B}^T \bold v_B = \begin{pmatrix} \bold B_x \cdot \bold R_x & \bold B_y \cdot \bold R_x & \bold B_z \cdot \bold R_x \\ \bold B_x \cdot \bold R_y & \bold B_y \cdot \bold R_y & \bold B_z \cdot \bold R_y \\ \bold B_x \cdot \bold R_z & \bold B_y \cdot \bold R_z & \bold B_z \cdot \bold R_z \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation34.png)
![[T]_{sat|inertiel} = [T]_{sat|orbite} [T]_{orbite|Terre} [T]_{Terre|inertiel}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation35.png)
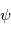 , autour de l'axe Oz, fait passer de (O,x,y,z) au référentiel (O,u,v,z) (en bleu).
, autour de l'axe Oz, fait passer de (O,x,y,z) au référentiel (O,u,v,z) (en bleu).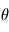 , autour de l'axe Ou (ligne des nœuds), fait passer de (O,u,v,z) à (O,u,w,z’) (en vert).
, autour de l'axe Ou (ligne des nœuds), fait passer de (O,u,v,z) à (O,u,w,z’) (en vert).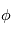 , ou rotation propre, autour de l'axe Oz’, fait passer de (O,u,w,z’) au référentiel lié au solide (O,x’,y’,z’) (en rouge).
, ou rotation propre, autour de l'axe Oz’, fait passer de (O,u,w,z’) au référentiel lié au solide (O,x’,y’,z’) (en rouge).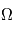 , autour de l'axe
, autour de l'axe  . La deuxième rotation est l'inclinaison,
. La deuxième rotation est l'inclinaison, 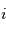 , autour de la ligne de noeuds. La dernière rotation est l'anomalie vraie,
, autour de la ligne de noeuds. La dernière rotation est l'anomalie vraie, 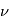 , autour de la normale à l'orbite.
, autour de la normale à l'orbite.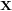 du satellite.
du satellite.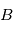 par rapport au référentiel
par rapport au référentiel 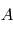 :
:
![[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation46.png)
![[T]_{B|A} = [T(\theta_1)]_1 [T(\theta_2)]_2 [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation47.png) , donc :
, donc : ![[T]_{B|A} = \begin{pmatrix} c_{\theta_2} c_{\theta_3} & c_{\theta_2} s_{\theta_3} & -s_{\theta_2} \\ s_{\theta_1} s_{\theta_2} c_{\theta_3} - c_{\theta_1} s_{\theta_3} & s_{\theta_1} s_{\theta_2} s_{\theta_3} + c_{\theta_1} c_{\theta_3} & s_{\theta_1} c_{\theta_2} \\ c_{\theta_1} s_{\theta_2} c_{\theta_3} +s_{\theta_1} s_{\theta_3} & c_{\theta_1} s_{\theta_2} s_{\theta_3} - s_{\theta_1} c_{\theta_3} & c_{\theta_1} c_{\theta_2} \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude/equation48.png)
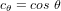 et
et 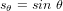 .
.

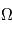 ), l'inclinaison (
), l'inclinaison (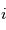 ) et l'anomalie vraie (
) et l'anomalie vraie (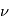 ).
).

 . C'est un vecteur unité possédant les mêmes composantes dans les référentiels de départ et d'arrivée :
. C'est un vecteur unité possédant les mêmes composantes dans les référentiels de départ et d'arrivée :  . Ainsi, 4 grandeurs sont requises pour décrire de façon non-ambigüe l'orientation par rapport à un référenciel : les 3 composantes de
. Ainsi, 4 grandeurs sont requises pour décrire de façon non-ambigüe l'orientation par rapport à un référenciel : les 3 composantes de  et l'angle de la rotation,
et l'angle de la rotation, 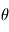 .
.
 . Le quaternion contient la même information qu'une MCD à 9 éléments, tout en s'affranchissant des problèmes de singularité rencontrés avec les angles d'Euler. Ils sont à la fois compacts et une représentation efficace de l'orientation pour la détermination d'attitude. Une même rotation est représentée par les quaternions
. Le quaternion contient la même information qu'une MCD à 9 éléments, tout en s'affranchissant des problèmes de singularité rencontrés avec les angles d'Euler. Ils sont à la fois compacts et une représentation efficace de l'orientation pour la détermination d'attitude. Une même rotation est représentée par les quaternions  et
et 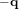 . On note également que les quatre paramètres d'Euler ne sont pas indépendants, mais contraints par la relation suivante :
. On note également que les quatre paramètres d'Euler ne sont pas indépendants, mais contraints par la relation suivante :
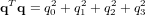
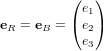 , les paramètres d'Euler sont :
, les paramètres d'Euler sont : 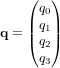 , avec
, avec 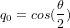 ,
, 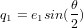 ,
, 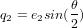 et
et 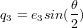 .
.
![[T]_{B|R} = [T(\bold q)] = \begin{pmatrix} 1-2(q_2^2+q_3^2) & 2(q_1q_2+q_3q_0) & 2(q_1 q_3 - q_2 q_0) \\ 2(q_2q_1-q_3q_0) & 1-2(q_1^2+q_3^2) & 2(q_2q_3+q_1q_0) \\ 2(q_3q_1+q_2q_0) & 2(q_3q_2-q_1q_0) & 1-2(q_1^2+q_2^2) \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude-quaternions/equation15.png)
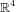 peut opérer sur un vecteur vivant lui dans
peut opérer sur un vecteur vivant lui dans 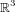 . Notons tout d'abord qu'un vecteur est un quaternion pur dont la partie réelle est nulle. L'opérateur
. Notons tout d'abord qu'un vecteur est un quaternion pur dont la partie réelle est nulle. L'opérateur 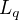 décrivant une rotation s'exprime avec le quaternion unitaire
décrivant une rotation s'exprime avec le quaternion unitaire  :
: 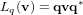 . Le vecteur ainsi obtenu conserve la longueur du vecteur initial, comme le fait une rotation. Cet opérateur se développe de la manière suivante :
. Le vecteur ainsi obtenu conserve la longueur du vecteur initial, comme le fait une rotation. Cet opérateur se développe de la manière suivante :
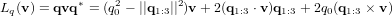
 et
et  décrivant respectivement les opérateurs
décrivant respectivement les opérateurs 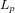 et
et 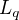 . Le premier opérateur est appliqué au vecteur
. Le premier opérateur est appliqué au vecteur  pour obtenir le vecteur
pour obtenir le vecteur 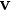 , puis le second est appliqué à
, puis le second est appliqué à 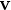 pour obtenir
pour obtenir 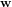 . La composition des opérateurs
. La composition des opérateurs 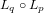 s'écrit :
s'écrit :
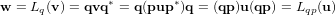
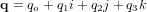
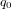 ,
, 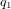 ,
, 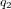 ,
, 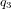 sont des nombres réels, et
sont des nombres réels, et 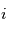 ,
, 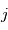 ,
, 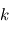 sont des symboles respectant les relations quaternioniques :
sont des symboles respectant les relations quaternioniques :
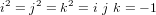
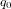 est appelé partie réelle de
est appelé partie réelle de  et
et 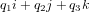 est appelé partie imaginaire.
est appelé partie imaginaire.
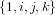 où s'applique l'addition composant par composant. Soient deux quaternions
où s'applique l'addition composant par composant. Soient deux quaternions  et
et  :
:
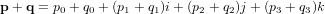
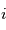 ,
, 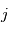 et
et 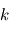 sont définis de la manière suivante :
sont définis de la manière suivante :
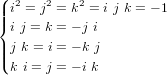
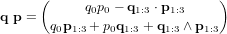
![\bold q \ \bold p = [Q(\bold q)] \bold p](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude-quaternions/equation53.png)
![[Q(\bold q)] = \begin{pmatrix} q_0 & -q_1 & -q_2 & -q_3 \\ q_1 & q_0 & -q_3 & q_2 \\ q_2 & q_3 & q_0 & -q_1 \\ q_3 & -q_2 & q_1 & q_0 \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-referentiels-et-transformations-representation-d-attitude-quaternions/equation54.png) .
.
 et
et  sont :
sont :
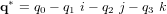 et
et 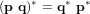
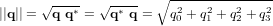 et
et 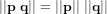
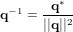
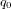 est la partie scalaire de
est la partie scalaire de  et
et 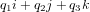 est la partie vectorielle. Ainsi, la partie scalaire est toujours réelle et la partie vectorielle toujours purement imaginaire. Bien que l'on ait dit qu'un quaternion est un vecteur dans un espace à 4 dimensions, il est courant de définir un vecteur pour la partie imaginaire d'un quaternion :
est la partie vectorielle. Ainsi, la partie scalaire est toujours réelle et la partie vectorielle toujours purement imaginaire. Bien que l'on ait dit qu'un quaternion est un vecteur dans un espace à 4 dimensions, il est courant de définir un vecteur pour la partie imaginaire d'un quaternion : 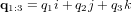 et
et