Maintenant que nous avons étudié les différentes façons de décrire l'orientation d'un repère à l'instant t, nous pouvons introduire la notion de mouvement. Les équations du mouvement sont un aspect essentiel de la conception et de la réalisation d'un système de contrôle d'attitude car elles régissent la position au cours du temps des objets considérés. Ces équations peuvent être séparées en deux catégories :
- Lorsque nous étudions l'orientation relative de deux référentiels en fonction du temps, nous sommes dans le domaine de la cinématique. Elle recouvre les aspects du mouvement qui peuvent être analysés sans considérer les forces et les couples.
- À l'instant où les forces et les couples sont introduits, on entre dans le domaine de la dynamique.
Afin de clarifier les choses, prenons une particule ponctuelle de la physique newtonienne. Si  représente sa position,
représente sa position, 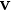 sa vitesse et que les dérivées temporelles sont indiquées par un point, alors l'équation cinématique du mouvement s'écrit
sa vitesse et que les dérivées temporelles sont indiquées par un point, alors l'équation cinématique du mouvement s'écrit  . L'équation dynamique du mouvement quant à elle s'écrit dans un repère galiléen
. L'équation dynamique du mouvement quant à elle s'écrit dans un repère galiléen 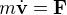 ou
ou  , avec
, avec 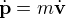 la quantité de mouvement,
la quantité de mouvement, 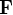 la résultante des forces appliquées et
la résultante des forces appliquées et 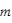 la masse de la particule. Comme vous le verrez par la suite, dès lors que l'on s'intéresse aux mouvement d'attitude (autour du centre d'inertie), les vecteur de position et de vitesse sont respectivement remplacés par la matrice d'attitude et le vecteur de vitesse angulaire
la masse de la particule. Comme vous le verrez par la suite, dès lors que l'on s'intéresse aux mouvement d'attitude (autour du centre d'inertie), les vecteur de position et de vitesse sont respectivement remplacés par la matrice d'attitude et le vecteur de vitesse angulaire 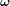 . Les forces et quantités de mouvement sont quant à elles remplacées par le couple
. Les forces et quantités de mouvement sont quant à elles remplacées par le couple  et le moment angulaire
et le moment angulaire  . La cinématique et la dynamique du mouvement rotationnel, ou d'attitude, sont plus compliquées que celles du mouvement de translation. Elles sont détaillées dans la section suivante.
. La cinématique et la dynamique du mouvement rotationnel, ou d'attitude, sont plus compliquées que celles du mouvement de translation. Elles sont détaillées dans la section suivante.
 Aller plus loin
Aller plus loin
La cinématique est l'étude du mouvement en fonction du temps indépendammant des causes produisant ce mouvement. Elle est utilisée pour décrire la trajectoire du centre de masse d'un satellite dans l'espace.
Cinématique et changement de référentiels
Dans notre domaine, nous sommes constamment contraints de passer d'un repère à un autre pour décrire la trajectoire d'un objet. En cas de référentiels en rotation, tels qu'un référentiel fixé par rapport à la Terre et un référentiel inertiel, passer de l'un à l'autre nécessite d'introduire des termes supplémentaires. Par exemple, si l'on veut décrire la position, la vitesse et l'accélération d'une particule dans un référentiel inertiel noté 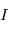 à partir de sa position dans un référentiel terrestre (fixé par rapport à la Terre) noté
à partir de sa position dans un référentiel terrestre (fixé par rapport à la Terre) noté 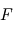 , on peut écrire :
, on peut écrire :
![\bold{r}_I = [T]_{I|F} \ \bold{r}_F](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation10.png)
![\bold{v}_I = \frac{d}{dt} (\bold{r}_I) = [T]_{I|F} \ \frac{d}{dt} (\bold{r}_F) + \frac{d}{dt}([T]_{I|F}) \ \bold{r}_F = [T]_{I|F} \ \frac{d}{dt}(\bold{r}_F) + ([T]_{I|F} \ [\Omega]) \ \bold{r}_F](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation11.png)
Nous avons utilisé la dérivée de la MCD qui est introduite dans le chapitre sur la cinématique d'attitude. Finalement :
![\bold{v}_I = [T]_{I/F} ([\Omega] \ \bold{r}_F + \bold{v}_F)](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation12.png)
![\bold{a}_I = \frac{d}{dt}(\bold{v}_I) = \frac{d}{dt}([T]_{I/F}) ([\Omega] \ \bold{r}_F + \bold{v}_F) + [T]_{I/F} \left[ \frac{d}{dt}([\Omega]) \ \bold{r}_F + [\Omega] \ \frac{d}{dt}(\bold{r}_F) + \frac{d}{dt}(\bold{v}_F)\right]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation13.png)
![\bold{a}_I = [T]_{I/F} \left[ [\Omega] \left([\Omega] \ \bold{r}_F \right) + 2 \ [\Omega] \ \bold{v}_F + \frac{d}{dt}([\Omega] \ \bold{r}_F + \bold{a}_F \right]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation14.png)
Dans le réferentiel en rotation (celui fixé par rapport à la Terre), la deuxième loi de Newton peut alors être écrite :
![\bold{F}_F = [T]_{F/I} \left( m \ \bold{a}_I \right) = m \left[ [\Omega] \left( [\Omega] \ \bold{r}_F \right) + 2 \ [\Omega] \ \bold{v}_F + \frac{d}{dt}([\Omega]) \ \bold{r}_F + \bold{a}_F \right]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation15.png)
où ![\frac{d}{dt} \left( [\Omega] \right)](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation16.png) est l'accélération angulaire. On introduit ici les accélérations centripète
est l'accélération angulaire. On introduit ici les accélérations centripète ![[\Omega] \left( [\Omega] \ \bold{r}_F \right)](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation17.png) et de Coriolis
et de Coriolis ![2 \ [\Omega] \ \bold{v}_F](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation18.png) .
.
La simulation et l'estimation d'attitude nécessitent généralement des représentations simples de l'attitude, telles que celles présentées dans le chapitre du même nom. Les équations différentielles de la cinématique peuvent ainsi être obtenues pour ces différentes représentations. Les démonstrations de ces équations sont proposées en exercices.
La cinématique d'attitude relie des vitesses angulaires à des orientations dans l'espace. Si cela peut sembler simple dans le cas d'une rotation autour d'un axe fixe, cela devient beaucoup moins intuitif dans le cas d'un mouvement plus général, où l'axe de rotation varie au cours du temps. Pour un corps en rotation autour d'un axe fixe, l'orientation par rapport à cet axe peut être déterminée en intégrant la vitesse angulaire ω, puisque 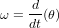 .
.
Quaternions
Dans le cas des quaternions, l'expression de l'équation de la cinématique se retrouve simplifiée :
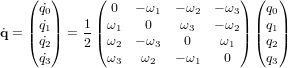
Une écriture plus compacte est possible :
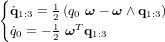
Contrairement aux angles d'Euler, les quaternions ne présentent pas de singularité géométrique. L'équation cinématique exprimée avec les quaternions ne possède pas de fonctions trigonométriques, ce qui rend les quaternions parfaitement adaptés aux calculs à bord réalisés en temps réel. Ainsi, les algorithmes de détermination d'attitude modernes sont généralement décrits en termes de quaternions.
Maintenant que nous nous tournons vers la dynamique d'attitude, il est important de bien différencier le mouvement de rotation d'un système du mouvement de son centre d'inertie. Nous allons nous concentrer sur le cas d'un corps rigide.
Propriétés d'inertie
Lorsque l'on parle du mouvement d'un solide autour de son centre d'inertie, il nous faut définir le tenseur d'inertie. Il s'exprime ainsi :
![[I] = \begin{pmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xz} & -I_{yz} & I_{zz} \end{pmatrix} = \begin{pmatrix} \sum_{i=1}^{n}{m_i \left(y_i^2+z_i^2 \right)} & -\sum_{i=1}^{n}{m_i \ x_i \ y_i} & -\sum_{i=1}^{n}{m_i \ x_i \ z_i} \\ -\sum_{i=1}^{n}{m_i \ x_i \ y_i} & \sum_{i=1}^{n}{m_i \left(x_i^2+z_i^2 \right)} & -\sum_{i=1}^{n}{m_i \ y_i \ z_i} \\ -\sum_{i=1}^{n}{m_i \ x_i \ z_i} & -\sum_{i=1}^{n}{m_i \ y_i \ z_i} & \sum_{i=1}^{n}{m_i \left(x_i^2+y_i^2 \right)} \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation9.png) ,
,
Les éléments diagonaux de ces expressions sont les moments d'inertie du solide par rapport aux divers axes, et les autres éléments sont les produits d'inertie. Les propriétés inertielles d'un solide sont donc totalement décrites par sa masse, la localisation de son centre d'inertie (ou centre de masse), et par les moments et produits d'inertie définis par rapport à des axes de références en un point particulier. Tous les solides ont un jeu d'axes principaux d'inertie dont l'origine se trouvent en son centre de masse et qui annule les produits d'inertie, rendant diagonale la matrice d'inertie.
 Appliquette interactive
Appliquette interactive
Une appliquette interactive est disponible ici. Elle illustre l'importance du choix des axes d'inertie dans le calcul de la matrice d'inertie.
 Rappel
Rappel
Considérons un satellite solide avec un référentiel fixé sur son corps 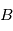 dont l'origine se trouve au centre de masse du satellite. Notons
dont l'origine se trouve au centre de masse du satellite. Notons 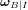 le vecteur vitesse angulaire du référentiel
le vecteur vitesse angulaire du référentiel 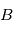 par rapport au référentiel inertiel
par rapport au référentiel inertiel 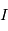 .
.
Equation d'Euler
D'après la 2ème loi de Newton, dans un référentiel galiléen, la dérivée de la quantité de mouvement est égale à la somme des forces extérieures qui s'exercent sur le solide. Dans le cas du moment angulaire, son principe de conservation stipule que sa dérivée est égale à la somme des couples extérieurs qui s'exercent sur le corps :
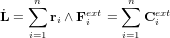
où 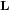 est le moment angulaire du corps solide par rapport à son centre de masse et
est le moment angulaire du corps solide par rapport à son centre de masse et 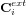 sont les couples extérieurs agissant sur ce corps. On appelle parfois cette équation l'équation d'Euler. Elle montre que seuls les couples extérieurs peuvent modifier le moment cinétique dans un système.
sont les couples extérieurs agissant sur ce corps. On appelle parfois cette équation l'équation d'Euler. Elle montre que seuls les couples extérieurs peuvent modifier le moment cinétique dans un système.
Facteurs impactant l'attitude d'un satellite
Il est maintenant possible de réécrire cette équation en reprenant l'expression du moment cinétique présentée précédemment complétée par le moment angulaire stocké par n'importe quel objet en rotation dans le satellite ![\bold L = [I] \boldsymbol\omega+ \bold h](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation28.png) :
:
![[I] \dot{\boldsymbol\omega} = \sum_{i=1}^{n}{\bold C_i^{ext} - \dot{\bold h} - \dot{[I]} \boldsymbol\omega}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation29.png)
Cette dernière équation permet de comprendre comment l'attitude d'un satellite peut être modifiée. En prenant les termes de cette équation de la gauche vers la droite, on retrouve d'abord les couples extérieurs, les objets embarqués en rotation (tels que les roues à inertie) et les modifications des moments d'inertie du satellite (qui peuvent notamment être dues à la perte de carburant au cours d'une mission).
En conclusion, les couples peuvent perturber l'attitude d'un satellite mais peuvent également être utilisés pour la contrôler. Les actionneurs doivent donc avoir une capacité suffisante pour contrer les couples perturbateurs tout au long de la mission si l'on veut un contrôle permanent de l'attitude du satellite.
 représente sa position,
représente sa position, 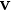 sa vitesse et que les dérivées temporelles sont indiquées par un point, alors l'équation cinématique du mouvement s'écrit
sa vitesse et que les dérivées temporelles sont indiquées par un point, alors l'équation cinématique du mouvement s'écrit  . L'équation dynamique du mouvement quant à elle s'écrit dans un repère galiléen
. L'équation dynamique du mouvement quant à elle s'écrit dans un repère galiléen 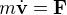 ou
ou  , avec
, avec 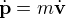 la quantité de mouvement,
la quantité de mouvement, 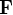 la résultante des forces appliquées et
la résultante des forces appliquées et 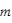 la masse de la particule. Comme vous le verrez par la suite, dès lors que l'on s'intéresse aux mouvement d'attitude (autour du centre d'inertie), les vecteur de position et de vitesse sont respectivement remplacés par la matrice d'attitude et le vecteur de vitesse angulaire
la masse de la particule. Comme vous le verrez par la suite, dès lors que l'on s'intéresse aux mouvement d'attitude (autour du centre d'inertie), les vecteur de position et de vitesse sont respectivement remplacés par la matrice d'attitude et le vecteur de vitesse angulaire 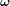 . Les forces et quantités de mouvement sont quant à elles remplacées par le couple
. Les forces et quantités de mouvement sont quant à elles remplacées par le couple  et le moment angulaire
et le moment angulaire  . La cinématique et la dynamique du mouvement rotationnel, ou d'attitude, sont plus compliquées que celles du mouvement de translation. Elles sont détaillées dans la section suivante.
. La cinématique et la dynamique du mouvement rotationnel, ou d'attitude, sont plus compliquées que celles du mouvement de translation. Elles sont détaillées dans la section suivante.
 allant de l'origine du repère au centre de l'objet
allant de l'origine du repère au centre de l'objet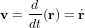
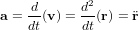
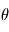 par rapport à sa position originelle
par rapport à sa position originelle est un vecteur unitaire dans la direction de l'axe de rotation, la vitesse angulaire est alors obtenue par :
est un vecteur unitaire dans la direction de l'axe de rotation, la vitesse angulaire est alors obtenue par : 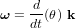
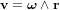
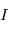 à partir de sa position dans un référentiel terrestre (fixé par rapport à la Terre) noté
à partir de sa position dans un référentiel terrestre (fixé par rapport à la Terre) noté 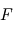 , on peut écrire :
, on peut écrire :
![\bold{r}_I = [T]_{I|F} \ \bold{r}_F](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation10.png)
![\bold{v}_I = \frac{d}{dt} (\bold{r}_I) = [T]_{I|F} \ \frac{d}{dt} (\bold{r}_F) + \frac{d}{dt}([T]_{I|F}) \ \bold{r}_F = [T]_{I|F} \ \frac{d}{dt}(\bold{r}_F) + ([T]_{I|F} \ [\Omega]) \ \bold{r}_F](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation11.png)
![\bold{v}_I = [T]_{I/F} ([\Omega] \ \bold{r}_F + \bold{v}_F)](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation12.png)
![\bold{a}_I = \frac{d}{dt}(\bold{v}_I) = \frac{d}{dt}([T]_{I/F}) ([\Omega] \ \bold{r}_F + \bold{v}_F) + [T]_{I/F} \left[ \frac{d}{dt}([\Omega]) \ \bold{r}_F + [\Omega] \ \frac{d}{dt}(\bold{r}_F) + \frac{d}{dt}(\bold{v}_F)\right]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation13.png)
![\bold{a}_I = [T]_{I/F} \left[ [\Omega] \left([\Omega] \ \bold{r}_F \right) + 2 \ [\Omega] \ \bold{v}_F + \frac{d}{dt}([\Omega] \ \bold{r}_F + \bold{a}_F \right]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation14.png)
![\bold{F}_F = [T]_{F/I} \left( m \ \bold{a}_I \right) = m \left[ [\Omega] \left( [\Omega] \ \bold{r}_F \right) + 2 \ [\Omega] \ \bold{v}_F + \frac{d}{dt}([\Omega]) \ \bold{r}_F + \bold{a}_F \right]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation15.png)
![\frac{d}{dt} \left( [\Omega] \right)](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation16.png) est l'accélération angulaire. On introduit ici les accélérations centripète
est l'accélération angulaire. On introduit ici les accélérations centripète ![[\Omega] \left( [\Omega] \ \bold{r}_F \right)](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation17.png) et de Coriolis
et de Coriolis ![2 \ [\Omega] \ \bold{v}_F](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation18.png) .
.
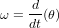 .
.
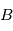 en rotation par rapport à un référentiel
en rotation par rapport à un référentiel 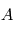 avec une vitesse angulaire
avec une vitesse angulaire 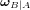 . Si la matrice d'attitude s'exprime
. Si la matrice d'attitude s'exprime ![[T]_{B|A}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation23.png) , alors :
, alors :
![\frac{d}{dt} \left( [T]_{B|A} \right) = -[\Omega] \ [T]_{B|A}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation24.png) avec
avec ![[\Omega] = \begin{pmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation25.png)
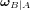 représentant la vitesse angulaire du référentiel
représentant la vitesse angulaire du référentiel 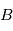 par rapport au référentiel
par rapport au référentiel 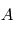 , avec
, avec 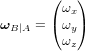 .
.
![[T(\theta_1)]_1 \leftarrow [T(\theta_2)]_2 \leftarrow [T(\theta_3)]_3](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-cinematique-du-satellite/equation30.png) conduisant du référentiel
conduisant du référentiel 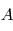 au référentiel
au référentiel 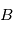 l'équation de la cinématique est réécrite :
l'équation de la cinématique est réécrite :
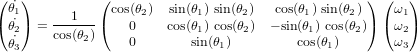
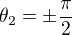 ).
).
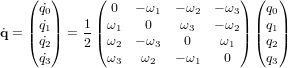
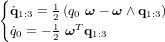
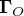 de la force
de la force 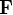 par rapport à au point
par rapport à au point 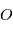 est défini par :
est défini par :
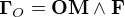
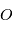 est non nul. Dans ce cas, il est possible de montrer que le moment global d'un tel couple par rapport à n'importe quel point est égal au produit vectoriel caractéristique du couple :
est non nul. Dans ce cas, il est possible de montrer que le moment global d'un tel couple par rapport à n'importe quel point est égal au produit vectoriel caractéristique du couple :
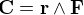
 est le vecteur allant du centre de gravité du système au point d'application de la force
est le vecteur allant du centre de gravité du système au point d'application de la force 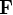 . Si, pour un corps solide sans contraine, une force va accélérer son centre de masse, un couple aura lui pour effet d'induire un mouvement de rotation autour du centre de masse.
. Si, pour un corps solide sans contraine, une force va accélérer son centre de masse, un couple aura lui pour effet d'induire un mouvement de rotation autour du centre de masse.
![[I] = \begin{pmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xz} & -I_{yz} & I_{zz} \end{pmatrix} = \begin{pmatrix} \sum_{i=1}^{n}{m_i \left(y_i^2+z_i^2 \right)} & -\sum_{i=1}^{n}{m_i \ x_i \ y_i} & -\sum_{i=1}^{n}{m_i \ x_i \ z_i} \\ -\sum_{i=1}^{n}{m_i \ x_i \ y_i} & \sum_{i=1}^{n}{m_i \left(x_i^2+z_i^2 \right)} & -\sum_{i=1}^{n}{m_i \ y_i \ z_i} \\ -\sum_{i=1}^{n}{m_i \ x_i \ z_i} & -\sum_{i=1}^{n}{m_i \ y_i \ z_i} & \sum_{i=1}^{n}{m_i \left(x_i^2+y_i^2 \right)} \end{pmatrix}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation9.png) ,
,
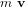 . Considérons un système matériel qui est la somme de
. Considérons un système matériel qui est la somme de 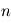 masses ponctuelles. Le moment angulaire, ou moment cinétique, par rapport à un point
masses ponctuelles. Le moment angulaire, ou moment cinétique, par rapport à un point 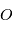 est le moment de la quantité de mouvement
est le moment de la quantité de mouvement  par rapport à ce point
par rapport à ce point 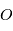 :
:
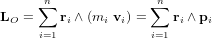
![[I]](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation16.png) et de la vitesse angulaire
et de la vitesse angulaire 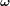 :
:
![\bold L = [I] \ \boldsymbol\omega](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation18.png)
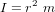 est le moment d'inertie d'une masse ponctuelle,
est le moment d'inertie d'une masse ponctuelle,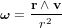 est le moment angulaire de la particule par rapport à l'origine.
est le moment angulaire de la particule par rapport à l'origine.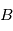 dont l'origine se trouve au centre de masse du satellite. Notons
dont l'origine se trouve au centre de masse du satellite. Notons 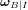 le vecteur vitesse angulaire du référentiel
le vecteur vitesse angulaire du référentiel 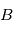 par rapport au référentiel inertiel
par rapport au référentiel inertiel 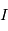 .
.
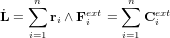
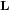 est le moment angulaire du corps solide par rapport à son centre de masse et
est le moment angulaire du corps solide par rapport à son centre de masse et 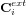 sont les couples extérieurs agissant sur ce corps. On appelle parfois cette équation l'équation d'Euler. Elle montre que seuls les couples extérieurs peuvent modifier le moment cinétique dans un système.
sont les couples extérieurs agissant sur ce corps. On appelle parfois cette équation l'équation d'Euler. Elle montre que seuls les couples extérieurs peuvent modifier le moment cinétique dans un système.
![\bold L = [I] \boldsymbol\omega+ \bold h](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation28.png) :
:
![[I] \dot{\boldsymbol\omega} = \sum_{i=1}^{n}{\bold C_i^{ext} - \dot{\bold h} - \dot{[I]} \boldsymbol\omega}](../pages_nanosats/equations_nanosats-comprendre-cinematique-et-dynamique-dynamique-du-satellite/equation29.png)