Modèles de Circulation Générale
Auteurs: Thomas Navarro, François Forget
- Découvrir
- Les premières idées de modélisation de l'atmosphère
- Les premiers modèles numériques
- L'utilisation des modèles aujourd'hui
- Comprendre
- Qu'est-ce qu'un GCM ?
- Du modèle physique au modèle numérique
- Structure d'un GCM
- Partie dynamique
- Discrétisation horizontale
- Le cœur dynamique
- Partie physique
- Discrétisation verticale
- Transfert radiatif
- Convection et turbulence
- Surface et sous-sol
- Aérosols et nuages
- Quelques spécificités
- En pratique
- Utiliser un GCM chez soi
- Autres types de modèles
- Se tester
- Mini Projet
- GCM en ligne
- Analyse des simulations
- Exploration des données
-
Modèles de circulation générale
L'étude des atmosphères des exoplanètes n'est pas uniquement limitée aux observations. On peut en effet faire des découvertes intéressantes au moyen de modèles qui simulent leur atmosphère. Ces modèles sont des outils informatiques complexes bien que reposant sur des lois physiques simples, issus de décennies de recherche dans la modélisation de l'atmosphère de la Terre, puis des planètes du système solaire.
Avant de suivre ce cours, il est conseillé d'avoir suivi les deux cours précédents sur l'atmosphère : dynamique et température.
Découvrir
Les premières idées de modélisation de l'atmosphère
Commençons par dresser une rapide chronologie de l'histoire des modèles numériques qui, bien que spécifique à l'atmosphère terrestre, nous éclaire sur leur démarche de compréhension de la réalité et qui sera reprise plus tard pour les planètes de notre système solaire, puis pour les exoplanètes.
Tout commence avec les développements de la physique des fluides au XIXe siècle, qui permet l'émergence d'un cadre scientifique et rigoureux pour poser les bases de la physique atmosphérique et la compréhension des mécanismes à l'œuvre dans l'atmosphère. Plus précisément, la formulation des équations primitives atmosphériques par Bjerknes en 1904 montre que l'écoulement de l'air dans l'atmosphère est régi par sept équations à sept inconnues. Dès lors, selon Bjerknes, prédire le devenir de l'atmosphère reviendrait à intégrer dans le temps ces équations en les initialisant avec des données provenant de stations de mesures météorologiques
Le problème décrit pas Bjerknes s'avère complexe : on ne sait pas résoudre ces équations analytiquement en raison de leur forte non-linéarité. En 1922, Richardson tente de surmonter ce problème en découpant une zone géographique d'étude en cellules où il intègre les équations primitives en les discrétisant avec la résolution de différences finies. Pour ce faire, les calculs sont résolus à la main, une tâche qui semblerait aujourd'hui bien fastidieuse.
Bien que son intuition et son ambition soient remarquables, son expérience « d'ordinateur humain » échoue à reproduire les résultats espérés de l'écoulement atmosphérique. En effet, son système d'équation ne prenait pas en compte des termes d'ondes atmosphériques à haute fréquence pourtant présentes à l'initialisation du problème, ce qui a conduit à la divergence de la solution. Son expérience ne sera tentée à nouveau qu'après l'avènement de l'ère informatique dans la seconde moitié du XXe siècle.
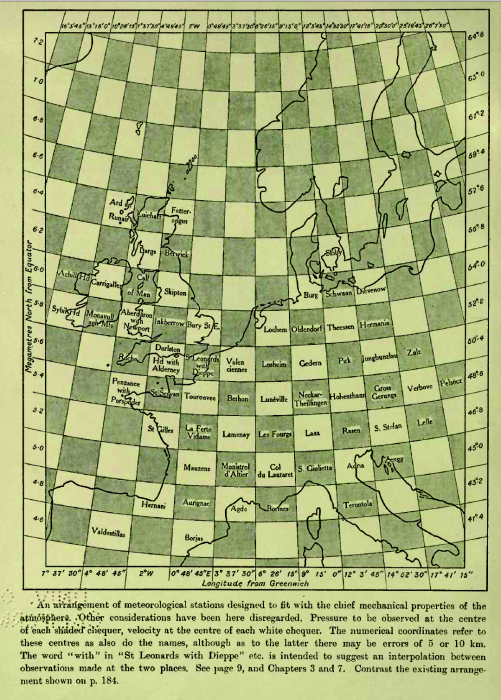
On peut voir sur cette page issue d'un travail de Richardson le découpage de l'atmophère en une grille régulière en Europe de l'Ouest. A chaque case correspond une ville se trouvant au plus proche du centre de la case pour mesurer la pression (cases noires) et le vent (cases blanches).
Crédit :
Charney 1951 / Google books
Les premiers modèles numériques
En 1948 et 1949, Charney, Fjørtoft et von Neuman réussirent la première prédiction météorologique à l'aide d'un modèle numérique. Pour ce faire ils utilisèrent uniquement l'équation de vorticité pour une atmosphère barotrope, c'est-à-dire supposée homogène, de densité uniforme et sans mouvement vertical. S'ensuivirent quelques années plus tard le premier service de prédiction météorologique en temps réel au moyen d'un modèle numérique par Rossby en 1954.
Ces expériences suggérèrent que l'intégration des équations primitives ne suffisait pas à modéliser toute l'atmosphère. En effet, ces équations sont l'équation de Navier-Stokes et une équation d'état pour l'air, appliquée sur une sphère en rotation. Charney propose de prendre en compte également les phénomènes physiques à plus petite échelle, tels que la condensation de l'eau, les radiations visibles et infrarouges et les flux turbulents de chaleur et de moment. La prise en compte de ces effets, au moyen de paramétrisations, a été depuis et demeure encore actuellement un sujet de recherche majeur dans la modélisation numérique de l'atmosphère.
Un exemple de prédiction atmosphérique
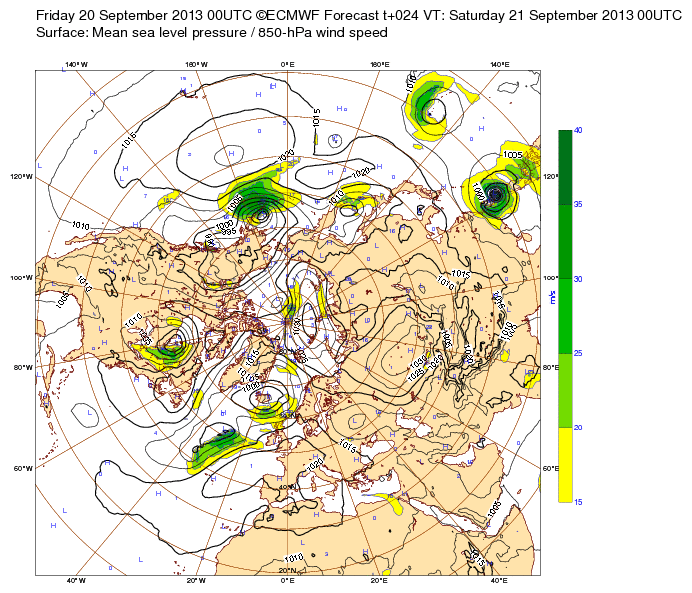
Les prévisions météorologiques s'appuient sur des résultats de simulations de modèles numériques d'atmosphères. L'exemple ci-dessus illustre une prédiction de vent (couleurs) et de pression de surface (contours).
Crédit :
ECMWF
L'utilisation des modèles aujourd'hui
Depuis les années 1950, de très nombreux groupes de recherche ont développé des modèles numériques pouvant simuler l'atmosphère de par le monde. Comme on vient de le voir, leur motivation première provient de la volonté de prédire l'écoulement de l'air, ou autrement dit sa circulation. Le nom donné à de tels modèles est MCG, pour Modèle de Circulation Générale, mais on utilise plus communément l'acronyme anglais GCM. Aujourd'hui les applications des GCMs se sont diversifiées : en plus de la prédiction météorologique, on les utilise pour étudier le climat de la Terre et les effets du changement climatique, les climats passés, présents et futurs d'autres planètes (Mars, Vénus, Jupiter, Saturne, Pluton) ou satellites (Titan, Triton) dotés d'une atmosphère dans le système solaire ainsi que du climat d'exoplanètes.
Les observations que nous possédons aujourd'hui sur les exoplanètes ne suffisent pas encore à contraindre précisémment un GCM. En effet, il faudrait une bonne connaissance de leur orbite, rayon, masse, etc ... et évidemment de leur topographie (pour les planètes telluriques) et composition atmosphérique pour être à même de simuler spécifiquement l'atmosphère d'une exoplanète. Le plus souvent, l'utilisation d'un GCM pour modéliser des atmosphères d'exoplanètes tient dans des études assez générales qui nous renseignent sur le comportement d'une atmosphère avec des hypothèses génériques. Toutefois, on constate qu'un nombre grandissant d'études visent à simuler l'état atmosphérique d'exoplanètes connues de la manière la plus fidèle possible afin d'interpréter au mieux les premières observations de leur atmosphère.
Pour l'étude de la Terre, le terme de GCM peut aussi bien faire référence à un modèle qui simule son atmosphère ou ses océans. Le couplage d'un modèle d'océan et d'atmosphère, avec également d'autres modèles pour la surface (hydrologie, végétation, glace d'eau) conduit à l'apparition d'un modèle qu'on qualifie de Global Climate Model, et dont les initiales restent GCM. Le terme de GCM est ainsi utilisé avec ambiguité et peut désigner un modèle d'atmosphère seul, d'océan seul, ou de l'addition d'un modèle d'atmosphère, d'océan et de surface.
Les initiales GCM peuvent indifférement vouloir dire Global Circulation Model ou Global Climate Model, mais on préférera le terme de climat à celui de circulation car bien souvent le but d'un GCM est de connaître le climat d'une exoplanète plutôt que sa circulation à un instant donné.
La planète Mars vue par le téléscope spatial Hubble

Ces quatre vues de la planète Mars montrent clairement la présence de nuages d'eau dans son atmosphère. Il est possible, grâce à un GCM, de simuler ces nuages et d'en apprendre plus sur leurs caractéristiques.
Crédit :
S. Lee, J. Bell, M. Wolff, HST, Nasa
Comprendre
Qu'est-ce qu'un GCM ?
Un GCM (Global Climate Model) est un modèle numérique dont le but est de simuler l'atmosphère d'un corps planétaire. L'ambition est de pouvoir reproduire toutes les observations instrumentales possibles, par exemple la température, les vents, etc ...
Le développement d'un GCM n'est jamais finalisé, et les accords aussi bien que les désaccords avec les observations disponibles poussent à améliorer le modèle, ce qui nous permet au passage d'en apprendre toujours plus sur les processus physiques à l'oeuvre dans le système climatique d'une corps planétaire.
Un GCM est basé sur un nombre limité d'équations, qui permet néanmoins d'atteindre un certain niveau de réalisme et de complexité. Il est fondamental de souligner que grâce à l'hypothèse d'universalité des lois de la physique, on arrive à adapter un GCM construit pour la Terre à d'autres corps dotés d'une atmosphère, moyennant un changement de certains paramètres (orbite, taille, composition, etc...), et l'ajout ou le retrait de certains processus physiques spécifiques au corps étudié. Par la suite, les explications sur la structure d'un GCM restent générales et ne sont pas, sauf mention autre, spécifiques à un corps en particulier.
Cette vidéo de l'Institut Pierre-Simon Laplace explique ce qu'est un GCM terrestre appliqué à la modélisation du climat.
Du modèle physique au modèle numérique
Une équation d'une loi physique comprenant une dérivée temporelle et/ou spatiale décrit l'évolution de variables continues avec le temps et/ou l'espace. On peut vouloir résoudre une telle équation au moyen de ressources informatiques, si par exemple sa résolution analytique est impossible ou si on veut l'intégrer à un ensemble plus complexe d'autres lois physiques. Pour ce faire, on procède à une discrétisation du temps et de l'espace, qui consiste à ne plus considérer les axes temporels ou spatiaux comme continus, mais au contraire comme un ensemble fini de valeurs. Ceci permet la discrétisation d'une équation, qui pourra dès lors être résolue par un ordinateur comme dans l'exemple suivant :
On utilise une grille régulière unidimensionnelle dont l'espacement entre deux points consécutifs est 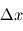 , qu'on appelle pas spatial. De même, deux instants consécutifs sont espacés d'une durée
, qu'on appelle pas spatial. De même, deux instants consécutifs sont espacés d'une durée 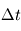 , qu'on appelle pas de temps.
On souhaite discrétiser sur cette grille un champ
, qu'on appelle pas de temps.
On souhaite discrétiser sur cette grille un champ 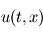 qui est solution de l'équation d'advection :
qui est solution de l'équation d'advection : 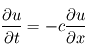 , avec
, avec 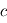 ayant la dimension d'une vitesse.
Pour procéder, on discrétise la variable
ayant la dimension d'une vitesse.
Pour procéder, on discrétise la variable 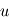 en un champ
en un champ 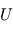 sur la grille, dont la valeur au j-ième point de la grille au n-ième instant t est notée
sur la grille, dont la valeur au j-ième point de la grille au n-ième instant t est notée 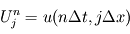 .
.
Une manière de discrétiser l'équation d'advection est de l'écrire: 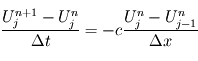 . Cette forme s'appelle un schéma amont.
. Cette forme s'appelle un schéma amont.
La manière d'écrire les différentielles peut être différente. Ainsi on aurait pu l'écrire sous la forme d'un schéma centré pour la dimension spatiale : 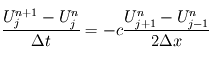 .
.
Ce qu'il faut retenir de cet exemple est que la discrétisation comporte une part d'arbitraire : il faut faire des choix, qui peuvent avoir des conséquences différentes sur la solution numérique finale.
Une équation discrétisée est donc une approximation de la véritable équation.
La première question de la discrétisation est de savoir si, pour reprendre l'exemple précédent, le champ discrétisé 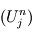 va tendre vers le champ analytique
va tendre vers le champ analytique 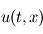 lorsque
lorsque 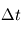 et
et 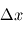 tendent vers zéro.
La deuxième question est de savoir à quel point la solution obtenue sera une approximation de la solution analytique. La manière de discrétiser puis utiliser une équation est une discipline en soi et il serait vain de vouloir introduire le sujet ici. Il faut juste garder à l'esprit qu'un GCM est un ensemble d'équations discrétisées, et par conséquent une approximation de la réalité. Cette approximation n'est pas du tout rédhibitoire et n'est pas le principal contributeur d'erreur d'un GCM. Toutefois, la discrétisation impose une règle forte sur le dimensionnement du GCM.
tendent vers zéro.
La deuxième question est de savoir à quel point la solution obtenue sera une approximation de la solution analytique. La manière de discrétiser puis utiliser une équation est une discipline en soi et il serait vain de vouloir introduire le sujet ici. Il faut juste garder à l'esprit qu'un GCM est un ensemble d'équations discrétisées, et par conséquent une approximation de la réalité. Cette approximation n'est pas du tout rédhibitoire et n'est pas le principal contributeur d'erreur d'un GCM. Toutefois, la discrétisation impose une règle forte sur le dimensionnement du GCM.
Cette règle, appelée condition de Courant-Friedrich-Lévy, repose sur le nombre de Courant :
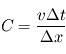 avec
avec 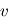 la vitesse maximale,
la vitesse maximale, 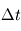 le pas de temps et
le pas de temps et 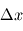 le pas d'espace.
Cette condition stipule que dans un cas simple ce nombre ne doit pas dépasser 1. Autrement dit, on choisit les pas de temps et d'espace tels qu'aucune particule d'air ne traverse plus d'une parcelle géométrique en un pas de temps. En pratique, l'utilisation de plusieurs équations dans un modèle, ainsi que l'utilisation de techniques de discrétisation plus poussées, font que cette simple condition n'est pas la seule à prendre en compte. Toutefois, cette condition demeure une limite forte et on aura toujours
le pas d'espace.
Cette condition stipule que dans un cas simple ce nombre ne doit pas dépasser 1. Autrement dit, on choisit les pas de temps et d'espace tels qu'aucune particule d'air ne traverse plus d'une parcelle géométrique en un pas de temps. En pratique, l'utilisation de plusieurs équations dans un modèle, ainsi que l'utilisation de techniques de discrétisation plus poussées, font que cette simple condition n'est pas la seule à prendre en compte. Toutefois, cette condition demeure une limite forte et on aura toujours 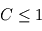 dans un GCM.
dans un GCM.
Structure d'un GCM
La structure d'un GCM peut se décomposer en "briques" indépendantes qui communiquent entre elles.
Du fait de l'universalité de ces équations, la nature de ces briques est la même quel que soit le corps étudié. La structure d'un GCM est en général composée des briques suivantes :
- Un "coeur" hydrodynamique
- Un transfert radiatif
- Une paramétrisation de la convection et de la turbulence à une échelle non résolue par le coeur hydrodynamique
- Un modèle thermique pour la surface et la sous-surface
- Un modèle d'évolution des nuages et aérosols
Étant donné que l'atmosphère est fortement stratifiée à grande échelle en vertu de l'équilibre hydrostatique, les longueurs caractéristiques horizontales et verticales ne sont pas les mêmes. Ceci permet de découper le GCM en deux parties différentes :
La première, appelée « dynamique », est le coeur hydrodynamique. Dans cette partie on calcule l'écoulement du fluide qu'est l'air autour d'un corps sphérique planétaire.
Elle consiste en l'implémentation des équations primitives et calcule la circulation atmosphérique. A un niveau vertical donné, les mouvements sont uniquement horizontaux. Le terme de "coeur" provient du fait que la partie dynamique sert à propager les mouvements à l'échelle horizontale, laquelle échelle domine la circulation globale de l'atmosphère.
La seconde, appelée « physique », rassemble tous les autres processus physiques à l'œuvre dans l'atmosphère sous forme de paramétrisation. Cela correspond donc au moins aux briques 2 à 5, mentionnées ci-dessus. La partie physique est une colonne verticale d'atmosphère : il s'agit d'un même modèle unidimensionnel démultiplié autant de fois qu'il existe de points dans la grille horizontale (donc dynamique) du modèle.
Les colonnes de la partie physique sont indépendantes les unes des autres et ne communiquent que via la partie dynamique par des mises à jour de pression, températures, vents et traceurs. On peut également voir la situation dans le sens inverse : la partie dynamique consiste en des couches sphériques imbriquées les unes dans les autres qui ne communiquent que via la partie physique.
Ce découpage en deux parties permet de faire appel à la partie physique moins souvent qu'à la partie dynamique, car les processus physiques en jeu ont des temps caractéristiques différents et donc des pas de temps d'intégration différents. Typiquement, on utilise la partie physique tous les 10 à 20 utilisations de la partie dynamique.
Structure d'un GCM
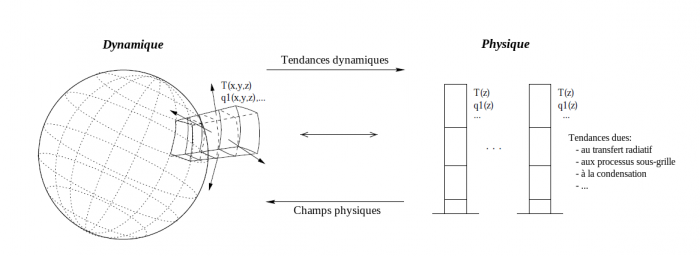
Ce schéma illustre le principe de fonctionnement et l'interface des parties physique et dynamique d'un GCM.
Crédit :
LMD
Partie dynamique
Discrétisation horizontale
Un GCM consiste en la discrétisation du temps en des instants régulièrement espacés (typiquement de l'ordre de la minute pour une planète comme la Terre) et en la discrétisation d'un espace tridimensionnel qu'on suppose être une sphère d'épaisseur mince. Il existe deux grandes manières de discrétiser la sphère pour les champs atmosphériques.
La première consiste à placer un certain nombre de points pour recouvrir la sphère, dans une méthode qu'on appelle différences finies. La deuxième consiste à discrétiser non pas en coordonnées géométriques, mais en coordonnées spectrales : les champs atmosphériques sont décomposés en harmoniques sphériques et tronqués au-delà d'une certaine harmonique. Dans ce dernier cas, il est nécessaire de faire la transformation des variables atmosphériques de l'espace fréquentiel vers l'espace géométrique avant l'appel à la partie physique et inversement.
En utilisant la méthode des différences finies, on peut trouver plusieurs façons de découper une sphère. Dans le cas d'une grille latitude-longitude, la dimension horizontale est tout simplement découpée en longitudes et latitudes également espacées, ce qui produira un point singulier à chaque pôle. Afin d'éviter ce problème on peut utiliser un découpage dit cube sphère, qui consiste en la projection d'un cube discrétisé sur la sphère, et donnera 8 points singuliers au lieu de deux dans le cas d'une grille latitude-longitude, mais qui seront plus simples à gérer. On peut également s'affranchir de tout point singulier au moyen d'un grille icosahédrique qui utilise des triangles pour couvrir la sphère. On peut imaginer d'autres manières de procéder, mais ces trois là constituent l'immense majorité des GCMs.
Le nombre et l'emplacement des points dans les dimensions horizontale et verticale restent fixés lors de l'exécution du programme informatique. Il est possible d'utiliser une résolution qui s'adapte aux conditions atmosphériques à un moment donné, mais cette particularité est encore (en 2017) peu répandue parmi les GCMs, et induit des complications qui font qu'on considérera que la résolution est fixée pour le reste de ce cours. On utilise le terme de résolution pour parler de la quantité de points utilisés dans la discrétisation spatiale. Ce terme s'utilise aussi dans le cas d'une discrétisation spectrale, et il correspond au nombre de modes employés dans la représentation des champs atmosphériques.
La résolution spatiale d'un GCM va typiquement de quelques centaines de kilomètres jusqu'à quelques milliers de kilomètres. Ce qui se passe en dessous de cette échelle n'est pas directement représenté. S'il s'avère nécessaire de tenir compte d'un processus qui se déroule à une échelle plus petite, une paramétrisation de ce processus est nécessaire, et est généralement intégrée dans la partie physique du modèle.
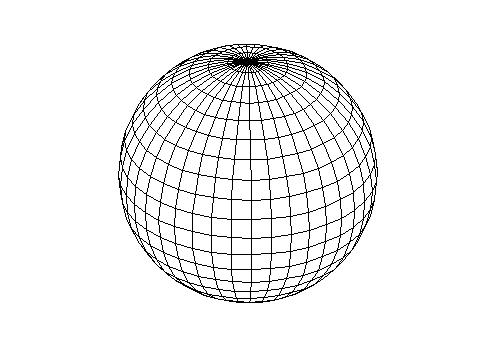
Grille latitude-longitude. Les pôles sont des points singuliers qu'il convient de traiter de manière particulière lors de la discrétisation des équations primitives sur cette grille.
Crédit :
MITgcm

Grille cube sphère. Chaque face d'un cube, déjà découpée, est projetée sur une sphère de même centre.
Crédit :
Bruno Luong
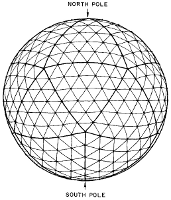
Grille icosahédrique. Chaque triangle peut être individuellement redécoupé en plus petits triangles.
Crédit :
Sadourny et al. 1969
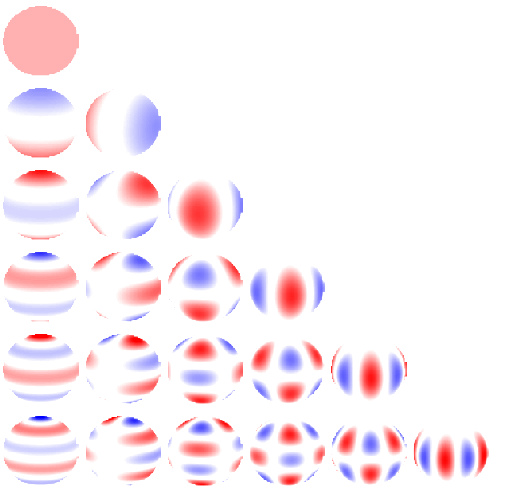
Discrétisation spectrale. On décompose chaque champ atmosphérique en harmoniques sphériques. L'avantage est d'éviter tout point singulier, mais il faut sans cesse faire la conversion sur une grille découpée spatialement, comme les trois autres évoquées ici, pour faire le lien avec la colonne physique. On voit ici à quoi correspondent les 21 premiers modes.
Crédit :
Benoit Moser. Lesia.
Le cœur dynamique
Le cœur hydrodynamique ou plus simplement partie dynamique d'un GCM consiste en la discrétisation des équations primitives sur la grille horizontale. Le but de la partie dynamique réside essentiellement dans le calcul des vents, de la température, ainsi que du transport des traceurs.
En général, plusieurs approximations sont faites dans ces équations qui nous viennent de l'étude de l'atmosphère terrestre, et qui doivent être remises en cause lorsqu 'appliquées à une autre atmosphère :
- L'équilibre hydrostatique est respecté, ce qui supprime toute onde acoustique verticale. Ceci ne pose pas de problème étant donnée la résolution d'un GCM, mais peut en poser en cas de vents verticaux très puissants, comme dans la partie haute de certaines atmosphères.
- L'épaisseur de l'atmosphère est petite devant le rayon planétaire. Un cas bien connu où cette approximation atteint ses limites est Titan, qui possède une atmosphère de 500 km d'épaisseur pour un rayon de 2575 km.
- La capacité calorifique de l'atmosphère est supposée constante, alors que le cas de Vénus nous montre qu'elle peut varier de 40 % selon l'altitude.
- La composition atmosphérique, et plus particulièrement sa masse molaire, est aussi supposée constante. Ceci n'est pas vrai dans les atmosphères où un composant majeur peut condenser, comme avec le CO2 sur Mars ou le N2 sur Pluton et Triton.
- Certaines quantités sont conservées au détriment d'autres. En effet, la quantité totale de masse, de moment angulaire, d'énergie, de température potentielle, de vorticitié potentielle et de traceur devraient toutes pouvoir être conservées. Hélas, ceci ne peut être le cas en raison de la discrétisation des équations primitives et des choix doivent être faits, qui dépendent du type d'atmosphère. Sans entrer dans les détails, on peut citer le cas des atmosphères en super-rotation (Vénus, Titan) qui requièrent de favoriser la conservation du moment cinétique.
Ainsi, le cœur hydrodynamique d'une planète autre que la Terre nécessite des adaptations et des généralisations par rapport à ce qui se fait depuis plus d'un demi-siècle dans le domaine de la modélisation terrestre. L'étude des planètes du système solaire a permis de mieux cerner ces généralisations, qui aujourd'hui s'appliquent aux exoplanètes.
Partie physique
Discrétisation verticale
On a vu qu'il existe différents types de discrétisation horizontale dans la partie dynamique. La discrétisation verticale pour la physique peut également varier d'un GCM à l'autre.
En général la dimension verticale, c'est-à-dire du bas vers le haut, fait intervenir la pression comme coordonnée naturelle plutôt que l'altitude. En effet, les dimensions horizontales d'un GCM sont telles que l'équilibre hydrostatique (voir ici) est toujours respecté, les fluctuations de pression autour de cet équilibre ne peuvent pas être représentées à l'échelle d'un GCM. Dès lors, la pression diminue de manière monotone avec l'altitude et constitue un système de coordonnées naturelles, d'autant plus qu'en vertu de l'équilibre hydrostatique, il existe un lien direct entre la pression et la masse d'atmosphère située au-dessus.
Le nombre de niveaux verticaux est de l'ordre de quelques dizaines, typiquement entre 20 au minimum pour représenter la circulation et 100 pour un modèle très résolu s'étendant très haut en altitude. À mesure que l'on monte en altitude, les niveaux sont de plus en plus espacés.
Ainsi, s'il arrive qu'à une altitude donnée la pression varie avec le temps, les niveaux verticaux suivront de fait cette variation. Pour les planètes telluriques, la topographie contrôle en grande partie la pression de surface, et il existe une représentation hybride qui tient compte de la topographie dans les plus basses couches de l'atmosphère, tout en se basant sur les niveaux de pression à plus haute altitude.
La question des limites du domaine représenté ne se pose par pour la grille dynamique, car elle représente une sphère. Pour la physique, l'extension verticale requiert de poser une limite en bas et en haut. La surface sert de limite dans le bas de l'atmosphère, et on impose les flux de masse verticaux en haut et en bas comme étant nuls. Ceci nécessite pour la limite haute la mise en place d'une couche-éponge pour éviter la réflection non réaliste d'ondes atmosphériques sur le plus haut niveau du modèle.
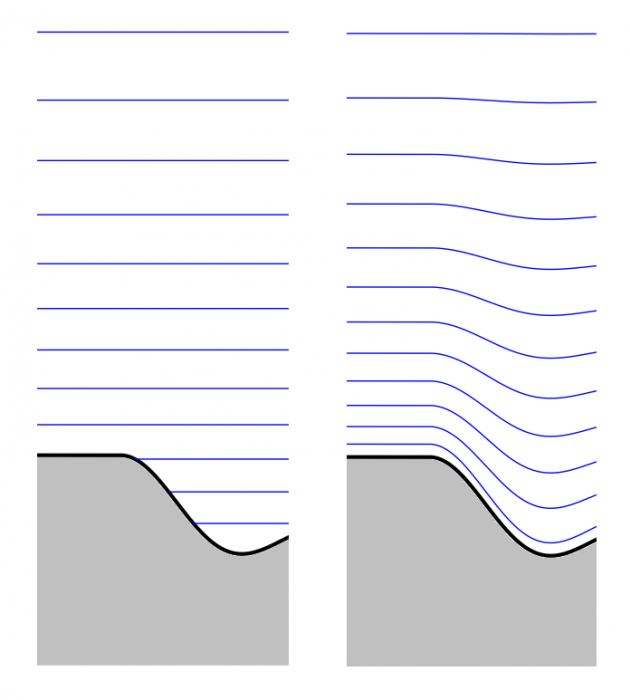
La discrétisation verticale en niveaux de pression ne tient pas compte de la topographie des planètes telluriques. Dans les plus basses couches de l'atmosphère, on peut utiliser une correction utilisant la pression de surface de manière progressive avec l'altitude .
Transfert radiatif
Le transfert radiatif dans un GCM est une paramétrisation qui vise à calculer l'impact du rayonnement sur l'atmosphère. In fine, le rayonnement donne lieu à des taux de chauffage ou de refroidissement de l'air, qui varient spatialement et temporellement. Le transfert radiatif est un point crucial pour le réalisme d'un GCM. En effet, il est le moteur de la circulation atmosphérique qui, en provoquant des gradients de température à l'échelle globale, va forcer tous les mouvements à grande échelle.
Le taux de chauffage ou de refroidissement atmosphérique provient de l'interaction entre d'une part le rayonnement et d'autre part deux entités :
- Les gaz qui composent l'atmosphère, qu'ils soient majoritaires ou minoritaires
- Les aérosols
Pour compliquer les choses, le connaissance du rayonnement lui-même dépend de ces deux entités. En haut de l'atmosphère, le rayonnement provient bien entendu de l'étoile. Dans l'atmosphère, ce rayonnement provient à la fois de l'étoile, en ayant été en partie absorbé ou diffusé par les gaz et les aérosols, et à la fois des gaz et aérosols eux-mêmes par émission thermique.
Il existe trois types de méthodes pour calculer le transfert radiatif à travers des gaz dans un GCM. Elles nécessitent avant tout une bonne connaissance du spectre du mélange de gaz présent dans l'atmosphère. Ce spectre est obtenu au moyen de simulateurs spécifiques, et vaut pour une température, une pression et une composition atmosphérique données. On pourrait d'abord naïvement tenter de calculer la contribution de chaque longueur d'onde au bilan radiatif global, mais c'est en pratique impossible car un tel calcul prendrait trop de temps pour les besoins d'un GCM. Au lieu de cela, il faut faire des simplifications. La plus simple est d'utiliser un modèle par bandes, dans lequel le flux radiatif est moyenné sur différents intervalles de longueurs d'onde. Une amélioration de cette méthode, appelée puissance nettes échangées, consiste à ne pas considérer les flux radiatifs du rayonnement, mais les échanges entre chaque niveau vertical de la colonne physique du GCM. Enfin, la méthode des distributions k-corrélées consiste à classer les lignes d'absorption du spectre par intensité croissante, puis à les interpoler par une fonction analytique. On passe ainsi de données spectrales très précises mais en nombre important et donc difficilement exploitables, à une approximation décrite par quelques paramètres et rapide en utilisation.
Le transfert radiatif des aérosols nécessite de connaître leur taille et leur composition afin de paramétriser leur effet sur la température atmosphérique. On peut employer les techniques précédemment décrites pour les gaz. Une technique largement employée est la division en bandes dans le spectre visible et infrarouge.
Pour aller plus loin, un GCM martien développé par la Nasa fournit une
documentation sur le transfert radiatif d'un modèle.
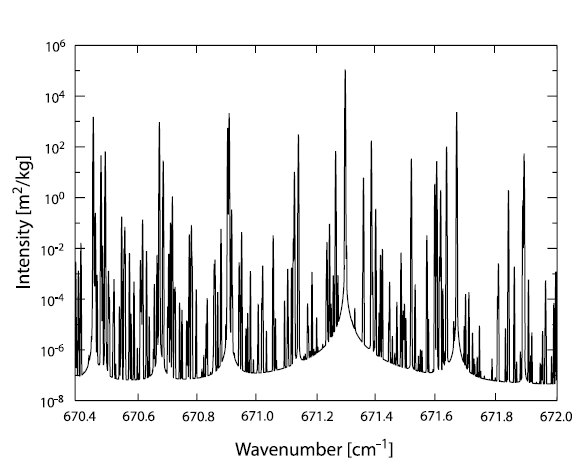
Une portion du spectre en absorption de l'air martien. On ne peut pas utiliser explicitement chaque ligne d'absorption dans le code radiatif. Un tel spectre doit être simplifié.
Crédit :
Mischna, Lee, Richardson 2012
Convection et turbulence
Certains processus de mélange de l'air interviennent à des échelles plus petites que celles résolues par la dynamique. Ces processus sont essentiellement la convection, qui peut se structurer en cellules de plusieurs de kilomètres, et la turbulence, qui agit depuis les échelles microscopiques jusqu'à quelques dizaines de mètres.
Une méthode simple pour représenter la convection consiste à utiliser un modèle dit d'ajustement convectif, qui va corriger le profil vertical de température vers un profil adiabatique stable. Autrement dit, on force la température potentielle à être constante là où le profil est instable. Bien que ce soit effectivement ce que la convection produit à grande échelle, un tel modèle ne tient pas compte des ascendances et descendances verticales dans la couche limite planétaire. De nouveaux modèles, appelés flux de masse, donnent une paramétrisation des mouvements d'air dans une parcelle physique de GCM. On peut ainsi tenir compte de la variation de densité de l'air si une espèce condense, ce qui va générer des mouvements verticaux.
La turbulence est le mouvement chaotique de l'air en dehors du régime laminaire. On en tient compte avec une paramétrisation qui donne l'effet des mouvements turbulents à grande échelle. Ceci est particulièrement pertinent pour les mouvements proche du sol, où la différence de température entre la surface chauffée par le soleil et l'atmosphère crée de la turbulence pendant le jour.
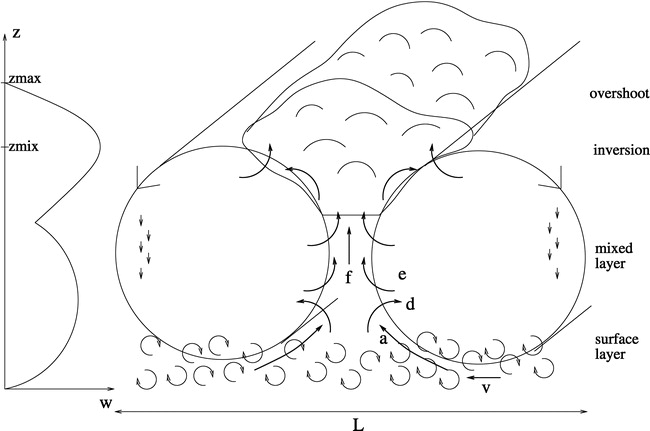
Ce schéma représente les flux de masse convectifs tels que paramétrisés dans un GCM. w : vitesse verticale. Le flux de masse f dépend de l'ascension a (depuis la surface) et e (au dessus), ainsi que de la descendance d.
Crédit :
Rio et Hourdin, 2008
Surface et sous-sol
Les planètes telluriques possédent une surface solide ou liquide avec laquelle l'atmosphère est en interaction. Ces interactions se font au travers des flux radiatifs (provenant de l'étoile, de l'atmosphère et de la surface), du transfert de chaleur entre l'air et la surface par convection, et la libération de chaleur par changement de phase d'un solide ou d'un liquide à la surface (typiquement, la condensation de la vapeur d'eau). La surface planétaire joue donc un rôle important dans le forçage de l'atmosphère à sa base.
La diffusion de chaleur dans le sous-sol joue un rôle à la surface, et il est nécessaire d'en tenir compte. Ainsi, de nombreux GCMs possèdent un modèle de sous-sol pour l'équation de diffusion de la chaleur, divisé en niveaux verticaux de plus en plus profonds (jusqu'à typiquement quelques mètres), de la même manière que l'atmosphère est représenté en niveaux verticaux de pression. Chaque niveau vertical a des propriétés qui dépendent des caractéristiques supposées du sous-sol.
Certains corps peu irradiés, comme Pluton et Triton, voient leur atmosphère dominée de manière importante par la surface et le sous-sol. Pour ces exemples, la chaleur stockée dans le sous-sol met plusieurs siècles à être restituée à la surface, ce qui nécessite une initialisation méticuleuse du modèle de sous-sol.
Cette approche de modélisation du sous-sol convient également dans le cas d'un océan liquide. Toutefois, un plus grand réalisme requiert de prendre en compte la circulation océanique, ce qui peut se faire grâce au couplage avec un modèle d'océan dédié.
Un GCM de planète gazeuse ne modélise évidemment pas la surface. Il se contente de représenter l'atmosphère jusqu'à une certaine pression, et utilise un forçage de flux radiatif, tout en imposant les flux verticaux de masse à zéro.

Image du sol martien transmise par la sonde Phoenix. On peut voir que le souffle des tuyères a mis à jour de la glace d'eau enfouie sous le sol. Cette glace est présente sur des portions importantes de Mars et possède une inertie thermique élevée qui doit être prise en compte dans un GCM.
Crédit :
Marco di Lorenzo, Kenneth Kremer, Nasa / JPL / UA / Max Planck Institute / Spaceflight
 Exercice
Exercice
Difficulté : ☆☆☆
L'équation de diffusion de la chaleur unidimensionnelle dans le sous-sol est donnée par ![C \frac{\partial T}{\partial t} = \frac{\partial}{\partial z} \left[ \lambda \frac{\partial T}{\partial z} \right]](../pages_circulation-globale/equations_gcm-comprendre-physique/equation1.png) avec
avec 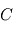 la capacité thermique volumique et
la capacité thermique volumique et 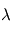 la conductivité thermique du matériau. On veut simuler au moyen d'un GCM une planète dont la surface est recouverte d'une épaisse couche de glace.
la conductivité thermique du matériau. On veut simuler au moyen d'un GCM une planète dont la surface est recouverte d'une épaisse couche de glace.
On prendra pour 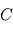 une valeur de 2 J.cm-3.K-1 et pour
une valeur de 2 J.cm-3.K-1 et pour 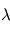 une valeur de 2.4 W.m-1.K-1, et on supposera les propriétés de la glace constantes et homogènes sur toute la planète.
une valeur de 2.4 W.m-1.K-1, et on supposera les propriétés de la glace constantes et homogènes sur toute la planète.
Question 1)
Sachant que sur cette planète une année dure 150 jours terrestres, quelle doit-être est la profondeur minimale du modèle de sous-sol ?
Question 2)
Comment faut-il espacer les niveaux verticaux du modèle de sous-sol ?
Analyser le champ de température 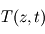 pour deux pulsations
pour deux pulsations 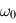 différentes
différentes
Aérosols et nuages
On a vu à quel point les aérosols jouent un rôle important en raison du transfert radiatif. Au-delà de leur impact sur les températures, leur étude en soi nous permet de mieux comprendre comment certaines espèces sont transportées à grande échelle et se déposent en surface.
Un aérosol est transporté horizontalement par la dynamique en tant que traceur. Dans la partie physique, on cherche à comprendre, en plus de leur effet radiatif, comment ils vont se former et se répartir sur l'axe vertical. Pour cela, on doit disposer d'une modélisation qui nous permette de calculer les tailles des particules des aérosols. Cette taille peut être établie de manière empirique, ou calculée à partir d'équations décrivant les processus de changement de phase.
Ces aérosols peuvent servir de noyaux de condensation (ou CCN) sur lesquels peuvent venir se condenser certaines espèces gazeuses, pour ensuite former des nuages. C'est par exemple le cas avec la formation de nuages d'eau (sous forme de cristaux de glace ou de gouttelettes liquides) sur Terre ou encore de nuages de glace de dioxyde de carbone (CO2) sur Mars. Sur certaines exoplanètes, on a même par exemple observé des nuages de chlorure de potassium ou de sulfure de zinc. Comme nous l'enseigne si bien la Terre, les nuages ont un rôle essentiel sur le bilan radiatif des planètes.
Lors d'un changement de phase (gaz → solide/liquide), la libération de chaleur latente doit également être prise en compte. La prise en compte de cet effet est notamment critique pour un GCM terrestre, étant données les grandes quantités d'eau pouvant s'évaporer ou se condenser dans l'atmosphère de notre planète. C'est par exemple un point clé pour comprendre l'échange de chaleur des basses vers les moyennes latitudes terrestres.
En pratique, la discrétisation d'un GCM repose sur des cellules de grande taille, qui représentent l'état moyen de l'atmosphère en leur sein. Pour représenter l'effet radiatif des nuages dans l'atmosphère d'une planète, il faut calculer proprement la fraction nuageuse dans chaque cellule du GCM, c'est-à-dire calculer la proportion (de la surface horizontale) de cette cellule où se trouve les nuages. Il existe un certain nombre de techniques plus ou moins sophistiquées qui permettent de traiter ce problème de recouvrement, mais cela dépasse le cadre de ce cours.

Des nuages de cristaux d'eau dans l'atmosphère de Mars vus par la sonde Phoenix.
Crédit :
Wikipédia

Ce cliché pris par la sonde Mariner 10 montre l'épaisse couche de nuages composée principalement d'un mélange H2SO4-H2O qui recouvre l'intégralité de Vénus.
Crédit :
Nasa
Quelques spécificités
À titre d'exemple, voici quelques spécificités propres à plusieurs corps planétaires, qui sont autant de "briques" à ajouter dans la partie physique :
- Un modèle de (photo)chimie, qui tient compte des réactions entre les différents composants de l'atmosphère. Il en résulte des changements de composition qui ont un impact sur l'atmosphère, par exemple au moyen du transfert radiatif. Pour modéliser l'atmosphère de Titan, le photochimie joue un rôle prépondérant. Pour modéliser l'atmosphère des exoplanètes géantes chaudes et gazeuses (les Jupiter chauds), c'est même la chimie hors équilibre qui devient importante.
- Les sources d'aérosols. Par exemple, Mars est une planète dont la structure thermique de l'atmosphère est complétement dominée par les poussières en suspension dans l'air. La quantité de poussière soulevée depuis le sol est une donnée importante pour la compréhension et la modélisation de l'atmosphère, qui peut donner lieu au développement d'un modèle spécifique.
- La thermosphère, qui est une région où les hypothèses classiques d'un fluide atmosphérique ne sont plus les mêmes. La densité est si faible que l'équilibre thermodynamique local, qui stipule que la température est spatialement homogène à l'échelle miscropscopique, n'est plus respecté. Ceci nécessite une adaptation du transfert radiatif.
En pratique
En pratique, un GCM est un programme informatique qui exécute des instructions résumées dans un code écrit dans un certain langage. En général, les modélisateurs optent pour le langage Fortran car il possède de nombreuses librairies mathématiques, est rapide dans l'exécution du programme généré, et on peut miser sur l'héritage de modèles plus anciens qui utilisaient eux aussi le Fortran il y plusieurs décennies.
Un GCM cumule au minimum des dizaines de milliers de lignes de code et requiert un investissement conséquent pour être développé et mis à jour.

Un exemple de code informatique en langage Fortran tel qu'utilisé dans la programmation d'un GCM. On voit ici la portion du programme où on a recours à la brique physique dont les tendances sont transmises à la brique dynamique.
Crédit :
LMD
Le temps de simulation est également un paramètre important à prendre en compte : on ne peut pas faire le même type d'étude selon qu'une simulation dure 5 minutes ou 5 mois. Dans le premier cas on peut par exemple envisager un nombre très important de simulations pour explorer la sensibilité du modèle à de multiples paramètres, tandis que dans le second cas la simulation sert de réference qui sera analysée en détail et on évitera à tout prix une erreur en amont, avant l'exécution du modèle. Il serait difficile de donner un chiffre typique sur le temps de simulation, étant donné qu'il dépend des ressources informatiques et de la résolution, du pas de temps, et de la configuration du modèle. Toutefois, afin de donner un ordre de grandeur, on peut avancer un rapport pouvant varier dans la plupart des cas de 100 à 10 000 entre le temps simulé et le temps réel d'exécution d'un GCM.
 Exercice
Exercice
Difficulté : ☆
Cet exercice a pour but d'estimer la taille d'un fichier de sortie d'une simulation de GCM.
Considérons un exemple représentatif : on simule une planète dont le jour solaire est de 24h et l'année dure 100 jours.
La grille utilisée est de type latitude-longitude, avec respectivement 48 et 64 points dans ces dimensions, et 20 niveaux verticaux.
Question 1)
Combien de points la grille contient-elle au total ?
Question 2)
On souhaite pourvoir étudier la circulation atmosphérique. Combien de variables utiliseriez-vous ?
Question 3)
Les variables sont écrites dans le fichier de sortie 6 fois par jour pour bien représenter le cycle diurne. Une valeur est représentée au moyen de 4 octets. Quelle est la taille informatique d'un fichier de sortie pour une année de simulation ? Qu'en pensez-vous ?
Utiliser un GCM chez soi
Il existe des dizaines et des dizaines de GCM différents de par le monde, utilisés avec des buts parfois différents. Un moyen simple d'utiliser soi-même un GCM est d'utiliser une version simplifiée, développée à des fins éducatives ou de validation. Leur prise en main est plus simple et plus rapide qu'un GCM classique, bien qu'il faille également y consacrer un certain temps pour installer, utiliser et interpréter le modèle.
On peut citer :
-
PLASIM (PLAnet SIMulator) qui peut être utilisé pour la Terre, Mars et Titan.
-
SPEEDY (Simplified Parameterizations, primitivE-Equation Dynamics) qui est un modèle à 7 niveaux verticaux pour l'atmosphère terrestre.
-
Climate prediction Un projet de science citoyenne qui propose d'utiliser les ressources de votre ordinateur pour générer des prédictions de changement climatique sur Terre.
-
Mars Climate Database Une base de données interactive issue d'un GCM martien.
LAPS Un modèle de climat 1-D interactif pour modéliser les atmosphères de planètes terrestres. Il correspond à la partie physique du GCM "Générique" développé au Laboratoire de Météorologie Dynamique, à Paris.
Autres types de modèles
De manière plus générale, il existe toute une hiérarchie de modèles numériques de climat qui permettent de simuler l'atmosphère des planètes. Par exemple, les modèles Mésoéchelle ou LES (pour Large Eddy Simulation) et modèles CRM (pour Cloud Resolving Model) permettent de simuler l'atmosphère à des échelles beaucoup plus fines que les GCM, afin de modéliser toutes les processus dynamiques et physiques qui y opèrent (par exemple la convection).
Ces types de modèles (Mésoéchelle, LES, CRM) sont très coûteux en temps de calcul du fait de leur résolutions spatiale et temporelle plus fines qu'un GCM. On les utilise généralement dans une région spécifique de la planète, pour comprendre et quantifier des mécanismes physiques qui ne peuvent pas être résolus par les GCMs. Ces types de modèles sont donc généralement utilisés de manière complémentaire aux GCMs, par exemple pour fournir des paramétrisations physiques de processus sous-maille aux GCMs.
Se tester
QCM 1
QCM 2
Exercices
 Exercice
Exercice
Question 1)
Vous oubliez de brancher la physique dans votre GCM de planète tellurique. Que peut-il se passer au niveau des résultats ?
 Exercice
Exercice
Question 1)
Vous avez un modèle de dimension N_longitude x N_latitude et vous passez 2N_longitude x 2N_latitude. Que faut-t-il faire pour respecter la condition CFL ? A priori, par combien sera multiplié le temps de calcul ?
Question 2)
On souhaite simuler avec un GCM une atmosphère de diazote pour une planète d'un rayon de 6000 km. On sait par ailleurs, en considérant le flux radiatif de l'étoile et sa distance à la planète, que la température maximale dans cette atmosphère n'excèdera pas 400 K. On demande à un étudiant d'effectuer une première simulation de cette atmosphère. L'étudiant propose d'utiliser une grille latitude-longitude avec 100 points en longitude et 100 points en latitude et un pas de temps dynamique de 20 minutes. On lui répond que sa simulation échouer. Pourquoi cela ?
Calculer la vitesse de l'onde la plus rapide ...
... puis appliquer la condition CFL.
Mini Projet
GCM en ligne
Ce mini projet vise à prendre en main un GCM à partir de résultats de simulations et d'une interface dédiée.
On se propose pour cela de voir la sensibilité d'un GCM, et tout particulièrement la circulation atmosphérique, à la période de rotation et à la taille d'une planète.
La configuration du modèle est la suivante :
- Grille longitude-latitude avec 64 points en longitude et 32 en latitude
- 15 niveaux verticaux en coordonnées pression
- Un rappel newtonien pour la physique
On se propose de voir la sensibilité de ce GCM à la période de rotation et à la taille de la planète.
Pour ce faire, on utilise 3 rayons et 6 périodes de rotations différentes, formant donc un total de 18 simulations.
Les variables disponibles en sortie sont :
- Température
- Vent zonal
- Vent méridien
- Pression de surface
- Flux de masse méridien
- Coefficient de super-rotation
Analyse des simulations
Pour chaque simulation, 60 pas de temps ont été stockés, avec une écriture de 1m 20s entre deux pas de temps :
 Exercice
Exercice
Question 1)
Calculer le temps nécessaire pour effectuer une simulation.
C'est aussi simple que ça.
Question 2)
Le coefficient de super-rotation est le rapport entre le vent zonal et la vitesse du sol due à la rotation de la planète. Comment exprime-t-on ce coefficient en fonction du vent et des caractéristiques de la planète ?
Question 3)
Calculer la taille occupée sur le disque par toutes les simulations.
Combien de simulations ?
Combien de variables par simulation ?
Combien de valeurs par variables ?
Combien d'octets pas valeur ?
Question 4)
Le calcul a été effectué grâce à un processeur cadencé à 3.6 GHz. Donner des arguments qui expliquent pourquoi les simulations ont été précalculées avant que vous ne les utilisiez. Quel est l'inconvénient ?
C'est une question de temps et de mémoire.
Un rappel newtonien a été utilisé pour simuler la partie physique. Cela consiste, à chaque appel à la physique, à relaxer le champ de température vers une température de référence imposée 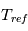 . On utilise la formulation donnée par Held & Suarez, Bulletin of the American Meteorological Society, vol. 75 , N°10, Octobre 1994. Le terme correctif est :
. On utilise la formulation donnée par Held & Suarez, Bulletin of the American Meteorological Society, vol. 75 , N°10, Octobre 1994. Le terme correctif est :
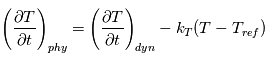
avec 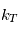 un coefficient de rappel dépendant de la latitude
un coefficient de rappel dépendant de la latitude 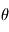 et de la coordonnée hybride
et de la coordonnée hybride 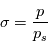 (où
(où 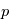 est la pression et
est la pression et 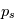 la pression de surface).
La loi pour
la pression de surface).
La loi pour 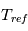 et
et 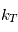 est :
est :
![T_{ref}(\theta,\sigma) = max \left[ 200, \left( 315 - 60\sin^2\theta -10 \ln (\sigma) \cos^2\theta \right) \sigma^\frac{2}{7}\right]](../pages_circulation-globale/equations_gcm-mini-projet/equation16.png)
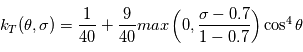
 Exercice
Exercice
Question 1)
Analyser l'expression de la température de référence 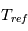 : comment varie-t-elle avec la latitude et l'altitude ?
: comment varie-t-elle avec la latitude et l'altitude ?
Physiquement, à quoi correspond 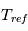 ?
?
Question 2)
Analyser l'expression du coefficient de rappel 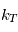 : comment varie-t-il avec la latitude et l'altitude ?
: comment varie-t-il avec la latitude et l'altitude ?
Pourquoi le rappel dépend-il ainsi de la latitude et de l'altitude ?
Question 3)
Comment sont représentés les jours et les saisons dans un GCM utilisant ce rappel newtonien ?
À quoi correspond la variable temporelle ?
Question 4)
Comment est modélisée la surface ?
Question 5)
Selon vous, pour quelles raisons utiliser ce rappel en lieu et place d'une physique plus complète ?
Exploration des données
Il s'agit de prendre en main les données et de se familiariser avec l'exploration de champs de 2 à 6 dimensions.
 Manuel de l'utilisateur
Manuel de l'utilisateur
L'interface de GCM en ligne permet d'afficher une variable du GCM. Chaque variable possède au plus 6 dimensions, tandis qu'une figure comporte 1 à 3 dimension(s) (une dimension suivant l'axe des abscisses obligatoirement, une dimension suivant l'axe des ordonnées, et une dimension temporelle pour le défilement). En effet, un être humain peut difficilement appréhender un jeu de données à plus de 3 dimensions d'un seul coup d'oeil. Pour visualiser une variable il s'agit donc de réduire le nombre de dimensions d'une variable. Pour cela on choisira, sur une à plusieurs dimensions, une valeur ou une moyenne sur un intervalle de valeurs.
| Dimensions | Nombre de valeurs | Valeurs | Remarques | Variables |
|---|
| Température | Vents | Pression de surface | Flux de masse | Super-rotation |
| Période de rotation | 6 | 5h - 10h - 24h - 72h - 240h - 2400h | Chaque valeur correspond
à une simulation différente | X | X | X | X | X |
| Rayon de la planète | 3 | 0.5, 1 et 2 rayons terrestres | X | X | X | X | X |
| Latitude | 48 | -90° à 90° | Vu le grand nombre de points,
l'interface sélectionne la valeur
la plus proche du curseur de la réglette | X | X | X | X | X |
| Longitude | 64 | -180° à 180° | X | X | X | | X |
| Altitude | 15 | 1 bar à 0.5 mbar | Valeurs suivant une
décroissance logarithmique | X | X | | X | X |
| Temps | 60 | 0 à 60 unités | | X | X | X | | X |
 Exercice
Exercice
Question 1)
Afficher la température et la pression de surface au niveau du sol, puis à d'autres altitudes à un instant donné ou en faisant défiler les instants sur un intervalle de temps. Comment évolue le champ de pression de surface en demandant différentes altitudes ? Pourquoi ?
Question 2)
Afficher un profil vertical de température à l'équateur.
Question 3)
Afficher le champ de température et la pression de surface en moyenne zonale, puis la température et le vent zonal. Que remarquez-vous ? Pourquoi ?
Question 4)
Un diagramme de Hovmöller permet de visualiser la propagation d'ondes, en affichant un champ en fonction du temps et de la longitude ou latitude. Faire un tel diagramme sur le champ de votre choix et estimer la ou les période(s) des ondes présentes.
Question 5)
Afficher la température en fonction de la latitude et de la vitesse de rotation, à une altitude donnée et en moyenne zonale.
Question 6)
Afficher la pression de surface en fonction de la vitesse de rotation et du rayon de la planète.
-------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------
ACCES AU PLAN DES CHAPITRES
Réponses aux QCM
pages_gcm-se-tester/gcm-qcm1.html
QCM
- Question 1
Solution : réponse 1)
(
Bien que correct, on préfère employer le terme de Climat à celui de Circulation car il reflète mieux l'usage d'un GCM pour une exoplanète. De plus, l'usage préfère le mot Global à Général.
)
Solution : réponse 2)
Solution : réponse 3)
(
Bien que correct, on préfère employer le terme de Climat à celui de Circulation car il reflète mieux l'usage d'un GCM pour une exoplanète.
)
pages_gcm-se-tester/gcm-qcm1.html
QCM
- Question 1
Solution : réponse 2)
- Question 2
Solution : réponse 1)
pages_gcm-se-tester/gcm-questions-qcm2.html
QCM
'Question de cours'
- Question 1
Solution : réponse 3)
- Question 2
Solution : réponse 3)
(
C'est vraiment la limite basse, qui est plutôt employée pour la Terre, dans des applications de prédiction météorologique.
)
Solution : réponse 4)
- Question 3
Solution : réponse 4)
- Question 4
Solution : réponse 1)
Réponses aux exercices
pages_circulation-globale/gcm-comprendre-surface.html
Exercice
- Question 1
Aide :
Considérer que le forçage au niveau de la température de surface s'écrit sous la forme 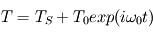 avec
avec 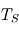 et
et 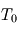 deux températures constantes et
deux températures constantes et 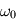 une pulsation...
une pulsation...
Aide :
...puis en déduire que le champ de température dans le sous-sol prend la forme 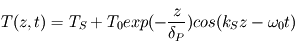 avec
avec 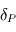 et
et 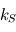 des termes dépendant de
des termes dépendant de 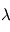 ,
, 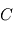 et
et 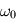
Solution :
On considère un forçage en surface correpondant à une pulsation 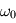 , de la forme
, de la forme 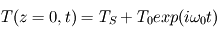 .
La solution s'écrit
.
La solution s'écrit 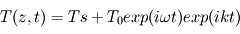 .
Par identification, on a donc
.
Par identification, on a donc 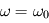 .
.
En appliquant l'équation de diffusion de la chaleur, on obtient la relation 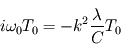 .
D'où les deux solutions
.
D'où les deux solutions 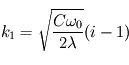 et
et 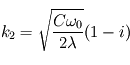
La solution avec 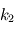 n'est pas physique, car elle donne une augmentation exponentielle du champ
n'est pas physique, car elle donne une augmentation exponentielle du champ 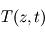 lorsque
lorsque 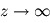 .
La solution finale s'écrit
.
La solution finale s'écrit 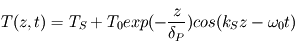 avec une fréquence spatiale
avec une fréquence spatiale 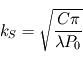 , une épaisseur de peau
, une épaisseur de peau 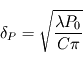 , et
, et 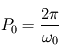
On se fixe comme critère que la profondeur minimale 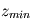 du sous-sol doit être telle qu'on représente le champ de température pour toutes les ondes :
du sous-sol doit être telle qu'on représente le champ de température pour toutes les ondes : 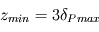 A priori, la période la plus élevée est la période annuelle (les cycles pluriannuels, plus subtiles, ne font pas partie de cette étude) :
A priori, la période la plus élevée est la période annuelle (les cycles pluriannuels, plus subtiles, ne font pas partie de cette étude) : 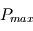 vaut 150 jours.
L'application numérique donne une profondeur minimale de 6,7 mètres.
vaut 150 jours.
L'application numérique donne une profondeur minimale de 6,7 mètres.
- Question 2
Aide :
Analyser le champ de température 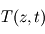 pour deux pulsations
pour deux pulsations 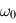 différentes
différentes
Solution :
L'épaisseur de peau 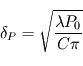 stipule que plus une onde a une période temporelle élevée, plus elle atteindra le sous-sol en profondeur. La période
stipule que plus une onde a une période temporelle élevée, plus elle atteindra le sous-sol en profondeur. La période 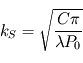 montre que plus une onde a une période temporelle élevée, moins sa période spatiale (suivant la profondeur) sera élevée. Ainsi, une discrétisation astucieuse requiert de rapprocher les niveaux proches de la surface, tandis que plus on ira en profondeur, plus les niveaux seront espacés.
montre que plus une onde a une période temporelle élevée, moins sa période spatiale (suivant la profondeur) sera élevée. Ainsi, une discrétisation astucieuse requiert de rapprocher les niveaux proches de la surface, tandis que plus on ira en profondeur, plus les niveaux seront espacés.
pages_circulation-globale/gcm-exercices.html
Exercice
pages_circulation-globale/analyse.html
Exercice
- Question 1
Aide :
C'est aussi simple que ça.
- Question 2
- Question 3
Aide :
Combien de simulations ?
Combien de variables par simulation ?
Combien de valeurs par variables ?
Combien d'octets pas valeur ?
- Question 4
Aide :
C'est une question de temps et de mémoire.



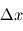 , qu'on appelle pas spatial. De même, deux instants consécutifs sont espacés d'une durée
, qu'on appelle pas spatial. De même, deux instants consécutifs sont espacés d'une durée 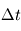 , qu'on appelle pas de temps.
On souhaite discrétiser sur cette grille un champ
, qu'on appelle pas de temps.
On souhaite discrétiser sur cette grille un champ 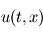 qui est solution de l'équation d'advection :
qui est solution de l'équation d'advection : 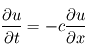 , avec
, avec 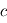 ayant la dimension d'une vitesse.
Pour procéder, on discrétise la variable
ayant la dimension d'une vitesse.
Pour procéder, on discrétise la variable 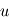 en un champ
en un champ 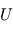 sur la grille, dont la valeur au j-ième point de la grille au n-ième instant t est notée
sur la grille, dont la valeur au j-ième point de la grille au n-ième instant t est notée 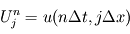 .
.
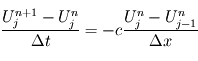 . Cette forme s'appelle un schéma amont.
. Cette forme s'appelle un schéma amont.
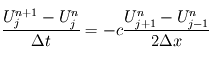 .
.
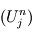 va tendre vers le champ analytique
va tendre vers le champ analytique 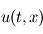 lorsque
lorsque 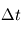 et
et 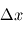 tendent vers zéro.
La deuxième question est de savoir à quel point la solution obtenue sera une approximation de la solution analytique. La manière de discrétiser puis utiliser une équation est une discipline en soi et il serait vain de vouloir introduire le sujet ici. Il faut juste garder à l'esprit qu'un GCM est un ensemble d'équations discrétisées, et par conséquent une approximation de la réalité. Cette approximation n'est pas du tout rédhibitoire et n'est pas le principal contributeur d'erreur d'un GCM. Toutefois, la discrétisation impose une règle forte sur le dimensionnement du GCM.
tendent vers zéro.
La deuxième question est de savoir à quel point la solution obtenue sera une approximation de la solution analytique. La manière de discrétiser puis utiliser une équation est une discipline en soi et il serait vain de vouloir introduire le sujet ici. Il faut juste garder à l'esprit qu'un GCM est un ensemble d'équations discrétisées, et par conséquent une approximation de la réalité. Cette approximation n'est pas du tout rédhibitoire et n'est pas le principal contributeur d'erreur d'un GCM. Toutefois, la discrétisation impose une règle forte sur le dimensionnement du GCM.
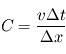 avec
avec 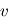 la vitesse maximale,
la vitesse maximale, 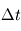 le pas de temps et
le pas de temps et 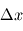 le pas d'espace.
Cette condition stipule que dans un cas simple ce nombre ne doit pas dépasser 1. Autrement dit, on choisit les pas de temps et d'espace tels qu'aucune particule d'air ne traverse plus d'une parcelle géométrique en un pas de temps. En pratique, l'utilisation de plusieurs équations dans un modèle, ainsi que l'utilisation de techniques de discrétisation plus poussées, font que cette simple condition n'est pas la seule à prendre en compte. Toutefois, cette condition demeure une limite forte et on aura toujours
le pas d'espace.
Cette condition stipule que dans un cas simple ce nombre ne doit pas dépasser 1. Autrement dit, on choisit les pas de temps et d'espace tels qu'aucune particule d'air ne traverse plus d'une parcelle géométrique en un pas de temps. En pratique, l'utilisation de plusieurs équations dans un modèle, ainsi que l'utilisation de techniques de discrétisation plus poussées, font que cette simple condition n'est pas la seule à prendre en compte. Toutefois, cette condition demeure une limite forte et on aura toujours 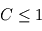 dans un GCM.
dans un GCM.









![C \frac{\partial T}{\partial t} = \frac{\partial}{\partial z} \left[ \lambda \frac{\partial T}{\partial z} \right]](../pages_circulation-globale/equations_gcm-comprendre-physique/equation1.png) avec
avec 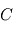 la capacité thermique volumique et
la capacité thermique volumique et 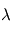 la conductivité thermique du matériau. On veut simuler au moyen d'un GCM une planète dont la surface est recouverte d'une épaisse couche de glace.
la conductivité thermique du matériau. On veut simuler au moyen d'un GCM une planète dont la surface est recouverte d'une épaisse couche de glace.
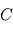 une valeur de 2 J.cm-3.K-1 et pour
une valeur de 2 J.cm-3.K-1 et pour 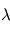 une valeur de 2.4 W.m-1.K-1, et on supposera les propriétés de la glace constantes et homogènes sur toute la planète.
une valeur de 2.4 W.m-1.K-1, et on supposera les propriétés de la glace constantes et homogènes sur toute la planète.
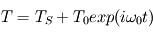 avec
avec 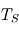 et
et 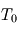 deux températures constantes et
deux températures constantes et 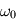 une pulsation...
une pulsation...
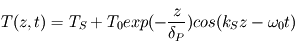 avec
avec 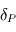 et
et 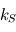 des termes dépendant de
des termes dépendant de 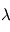 ,
, 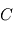 et
et 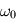
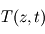 pour deux pulsations
pour deux pulsations 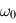 différentes
différentes



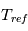 . On utilise la formulation donnée par Held & Suarez, Bulletin of the American Meteorological Society, vol. 75 , N°10, Octobre 1994. Le terme correctif est :
. On utilise la formulation donnée par Held & Suarez, Bulletin of the American Meteorological Society, vol. 75 , N°10, Octobre 1994. Le terme correctif est :
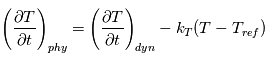
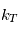 un coefficient de rappel dépendant de la latitude
un coefficient de rappel dépendant de la latitude 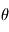 et de la coordonnée hybride
et de la coordonnée hybride 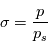 (où
(où 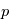 est la pression et
est la pression et 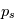 la pression de surface).
La loi pour
la pression de surface).
La loi pour 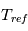 et
et 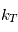 est :
est :
![T_{ref}(\theta,\sigma) = max \left[ 200, \left( 315 - 60\sin^2\theta -10 \ln (\sigma) \cos^2\theta \right) \sigma^\frac{2}{7}\right]](../pages_circulation-globale/equations_gcm-mini-projet/equation16.png)
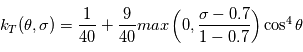
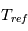 : comment varie-t-elle avec la latitude et l'altitude ?
: comment varie-t-elle avec la latitude et l'altitude ?
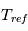 ?
?
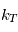 : comment varie-t-il avec la latitude et l'altitude ?
: comment varie-t-il avec la latitude et l'altitude ?
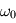 , de la forme
, de la forme 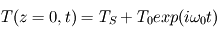 .
La solution s'écrit
.
La solution s'écrit 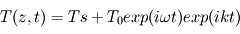 .
Par identification, on a donc
.
Par identification, on a donc 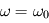 .
.
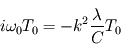 .
D'où les deux solutions
.
D'où les deux solutions 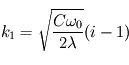 et
et 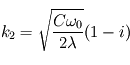
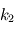 n'est pas physique, car elle donne une augmentation exponentielle du champ
n'est pas physique, car elle donne une augmentation exponentielle du champ 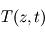 lorsque
lorsque 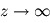 .
La solution finale s'écrit
.
La solution finale s'écrit 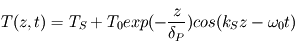 avec une fréquence spatiale
avec une fréquence spatiale 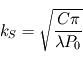 , une épaisseur de peau
, une épaisseur de peau 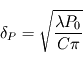 , et
, et 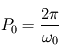
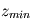 du sous-sol doit être telle qu'on représente le champ de température pour toutes les ondes :
du sous-sol doit être telle qu'on représente le champ de température pour toutes les ondes : 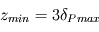 A priori, la période la plus élevée est la période annuelle (les cycles pluriannuels, plus subtiles, ne font pas partie de cette étude) :
A priori, la période la plus élevée est la période annuelle (les cycles pluriannuels, plus subtiles, ne font pas partie de cette étude) : 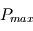 vaut 150 jours.
L'application numérique donne une profondeur minimale de 6,7 mètres.
vaut 150 jours.
L'application numérique donne une profondeur minimale de 6,7 mètres.
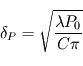 stipule que plus une onde a une période temporelle élevée, plus elle atteindra le sous-sol en profondeur. La période
stipule que plus une onde a une période temporelle élevée, plus elle atteindra le sous-sol en profondeur. La période 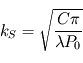 montre que plus une onde a une période temporelle élevée, moins sa période spatiale (suivant la profondeur) sera élevée. Ainsi, une discrétisation astucieuse requiert de rapprocher les niveaux proches de la surface, tandis que plus on ira en profondeur, plus les niveaux seront espacés.
montre que plus une onde a une période temporelle élevée, moins sa période spatiale (suivant la profondeur) sera élevée. Ainsi, une discrétisation astucieuse requiert de rapprocher les niveaux proches de la surface, tandis que plus on ira en profondeur, plus les niveaux seront espacés.