| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Dynamique d'un disque de planétésimaux |
Une population de planétésimaux orbitant le soleil ne pourra former des corps plus massifs que si les vitesses de rencontres mutuelles 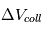 sont, pour une fraction importante de ces rencontres, inférieures à
sont, pour une fraction importante de ces rencontres, inférieures à 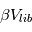 ; où
; où 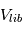 est la vitesse de libération à la surface de 2 planétésimaux en collision et
est la vitesse de libération à la surface de 2 planétésimaux en collision et 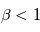 un paramètre prenant en compte la dispersion d’énergie lors de l’impact. Toute la question est alors de savoir si, effectivement, ce critère
un paramètre prenant en compte la dispersion d’énergie lors de l’impact. Toute la question est alors de savoir si, effectivement, ce critère 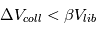 va être rempli dans un disque de planétésimaux kilométriques laissé à lui même.
va être rempli dans un disque de planétésimaux kilométriques laissé à lui même.
L’état dynamique d’un tel disque va dépendre de l’équilibre entre plusieurs mécanismes: la gravité mutuelle des planétésimaux, la force de friction du gaz primordial toujours présent à ce stade, la dissipation d’énergie lors des collisions physiques, et, bien sur, la gravité de l’étoile autour de laquelle tous les corps orbitent. Si on fait l’hypothèse simplificatrice que tous les planétésimaux ont la même taille 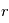 , alors on peut montrer que le disque va tendre vers un état stationnaire où les vitesses de rencontres vont en moyenne être de l’ordre de
, alors on peut montrer que le disque va tendre vers un état stationnaire où les vitesses de rencontres vont en moyenne être de l’ordre de 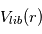 . Si en effet
. Si en effet 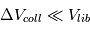 , alors les déflections gravitationnelles lors de rencontres proches vont automatiquement augmenter
, alors les déflections gravitationnelles lors de rencontres proches vont automatiquement augmenter 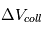 . Et si, à l’inverse,
. Et si, à l’inverse, 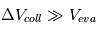 , alors la dissipation d’énergie cinétique lors des collisions va être très forte et fera diminuer
, alors la dissipation d’énergie cinétique lors des collisions va être très forte et fera diminuer 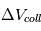 . Cet équilibre autour de
. Cet équilibre autour de 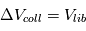 est plutôt une bonne nouvelle, car il entraine qu’une fraction des collisions vont effectivement permettre l’accrétion des corps (sachant qu’il y aura toujours une dispersion des vitesses de collision autour leur valeur moyenne).
est plutôt une bonne nouvelle, car il entraine qu’une fraction des collisions vont effectivement permettre l’accrétion des corps (sachant qu’il y aura toujours une dispersion des vitesses de collision autour leur valeur moyenne).
Sachant que tous ces corps sont en orbite autour d’une étoile, par exemple le Soleil, les vitesses relatives de collisions vont être directement liées à l’excentricité (et à leur inclinaison si on est en 3D) de leurs orbites : plus les orbites sont excentriques, plus 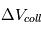 augmente, plus elles sont circulaires, plus
augmente, plus elles sont circulaires, plus 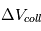 tend vers zero. Pour de petites excentricités, à l’ordre zero on peut écrire que
tend vers zero. Pour de petites excentricités, à l’ordre zero on peut écrire que
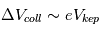
Il faut réaliser que, pour des planétésimaux kilométriques, on a affaire à des vitesses très faibles, car les 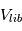 de tels corps sont de l’ordre de quelques mètres par seconde seulement. Ceci se traduit par des excentricités orbitales très faibles, de l’ordre de 0.0001 ! (cf. exercice).
de tels corps sont de l’ordre de quelques mètres par seconde seulement. Ceci se traduit par des excentricités orbitales très faibles, de l’ordre de 0.0001 ! (cf. exercice).