Accrétion «Boule de neige»

Auteur: Philippe Thébault

Accrétion boule de neige : un corps initialement plus gros que les planétésimaux qui l‘entourent va légèrement infléchir la trajectoire de ceux-ci vers lui (Figure A). De ce fait, il va croître plus rapidement que les corps qui l’entourent, ce qui va encore accentuer sa tendance à infléchir vers lui l’orbite de ceux-ci (Figure B). Le processus s’auto-amplifie de lui même et conduit à la formation rapide d’un embryon planétaire alors que la majorité des autres planétésimaux n’a pas accrété de matière (Figure C).

Crédit : Philippe Thebault

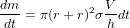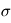Si tous les planétésimaux du disque avaient exactement la même taille r et grandissaient tous à la même vitesse, alors leur taux de croissance serait égal à $\frac{dm}{dt} = \pi (r+r)^2 \sigma \frac{V}{h} dt$ où $\sigma$ est la densité surfacique de planétésimaux, 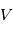leur vitesse relative de collision et 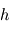l’épaisseur du disque. Si on fait l’approximation raisonnable que 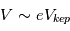$V \sim e V_{kep}$ (cf. 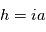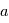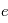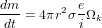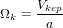page précédente) et que h = i a (, distance à l’étoile et excentricité moyenne de l’orbite des planétésimaux), alors on obtient $\frac{dm}{dt} = 4 \pi r^2 \sigma \frac{e}{i} \Omega_k$ avec $\Omega_k = \frac{V_{kep}}{a}$ , vitesse angulaire Keplerienne. On trouve alors que 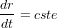$\frac{dr}{dt} = cste$ , et que la croissance en taille est linéaire avec le temps. Pour une MMSN à 1UA on trouve qu’il faut alors quelques 10⁶ ans pour former un corps de 1000km (cf. EXERCICE)

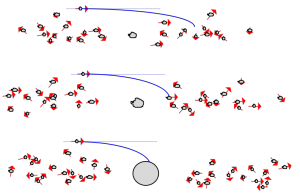
Mais il semble qu’en réalité l’accrétion suive un chemin beaucoup plus rapide et efficace, mais très sélectif, appelé accrétion « boule de neige ». Il est en effet plus que probable que, dans tout disque réel, toutes les tailles ne sont pas identiques et que, localement, certains planétésimaux soient, par hasard, légèrement plus grands (de taille 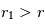r_1>r ) que ceux qui les entourent. De ce fait, ils ont une vitesse de libération 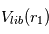$V_{lib}(r_1)$ supérieure à celle des corps environnants. En conséquence, ils vont légèrement infléchir la trajectoire des autres corps vers eux. On peut paramétriser cette déflection en considérant que le corps 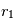r_1 a une section efficace « effective » 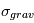$\sigma_{grav}$ plus grande que sa simple section efficace géométrique 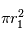$\pi r_1^2$ . On a alors

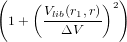$\Sigma = \pi (r_1+r)^2 \left [ 1+ \left (\frac{V_{lib}(r_1,r)}{\Delta V} \right )^ 2\right ]$

Où $\left (1+ \left (\frac{V_{lib}(r_1,r)}{\Delta V} \right )^ 2 \right )$ est appelé le terme de « focalisation gravitationnelle ». Du fait de cette surface efficace« dilatée », le corps 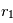r_1 va croître plus vite que les autres. Le rapport 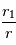$\frac{r_1}{r}$ va donc augmenter, ce qui a pour effet d’encore augmenter la focalisation gravitationnelle, et donc le taux de croissance de 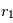r_1 , et ainsi de suite. La croissance de ce corps initialement légèrement privilégié va donc rapidement s’emballer.