Photo-évaporation et dispersion du gaz

Auteur: Philippe Thébault

images/Approfondissement-5-PHOTOEVAP.png

Différentes étapes du processus de dispersion d’un disque proto-planétaire gazeux par photoevaporation et accrétion visqueuse du disque.

Crédit : Observatoire de Paris

L’un des moyens les plus efficaces pour disperser le disque de gaz en moins de 10 millions d’années (voir la page de cours) est le couplage entre (l'accrétion visqueuse du disque) et la photo-évaporation du gaz. Ce dernier mécanisme est la conséquence de l’effet du rayonnement ultra-violet (UV) de l’étoile sur les molécules de gaz, essentiellemen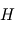t et 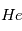. L’interaction des photons UV va en effet chauffer le gaz, c’est à dire lui donner une plus grande agitation thermique, et si cette vitesse d’agitation thermique dépasse la vitesse Képlerienne locale, alors le gaz est éjecté. 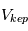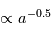Comme $V_{kep}$ est $\propto a^{-0.5}$ mais que l’énergie transportée par un photon UV ne diminue pas avec la distance à l’étoile, ce sont les molécules des régions extérieures qui seront le plus facilement éjectées lors d’interaction photon-gaz (mais le flux de photon, et donc le taux d’interaction avec le gaz, va, lui, diminuer avec 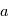). On peut ainsi calculer qu’il existe un rayon critique, appelée 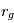r_g , au delà duquel l’énergie déposée par photo-évaporation dépasse l’énergie orbitale :

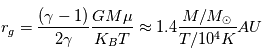
$r_g = \frac{(\gamma -1)}{2\gamma} \frac{GM \mu}{K_B T} \approx 1.4 \frac{M/M_{\odot}}{T/10^4 K} AU$

Où 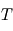est la température du gaz par suite de l’interaction avec un photon, 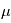$\mu$ est le poids atomique moyen du gaz, 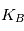K_B la constante de Boltzman, 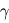$\gamma$ le ratio des chaleurs spécifiques (5/3 pour un gaz mono-atomique), 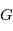la constante gravitationnelle et 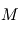la masse de l’étoile. Dans les faits, à cause de la rotation du gaz, le rayon critique de dispersion est plutôt égal à 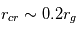$r_{cr} \sim 0.2 r_g$ . Pour un rayonnement UV typique, on a 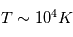$T \sim 10^4 K$ . 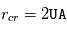Pour une étoile de type solaire et un disque de type MMSN , on obtient alors $r_{cr} = 2 \verb?UA?$ .

Cependant, tant que le disque est très dense, à la distance 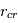$r_{cr}$ le flux de matière 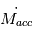$\dot{M_{acc}}$ vers l’intérieur du disque dû à la viscosité est supérieur au flux de matière 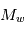M_w éjecté par photo-évaporation (cf. IMAGE, CASE 1). Mais à mesure que la masse du disque diminue par accrétion sur l’étoile, 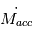$\dot{M_{acc}}$ va décroître, jusqu’à ce qu’on atteigne le point où 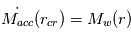$\dot{M_{acc}}(r_{cr}) = M_w(r)$ . A partir de ce moment, la matière gazeuse au-delà de 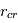$r_{cr}$ est éjectée du système avant de pouvoir franchir la frontière 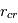$r_{cr}$ pour se mettre « à l’abri ». Une ouverture est alors créée dans le disque, qui se retrouve coupé en deux. La partie interne du disque est protégée de la photo-évaporation, mais est tellement petite (<2UA) qu’elle va très rapidement être accrétée sur l’étoile (alors qu’auparavant le flux de matière spirallant sur l’étoile était compensé par de la matière venant de plus loin dans le disque). La partie externe du disque va elle se disperser progressivement de l’intérieur ( 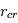$r_{cr}$ ) vers l’extérieur. Les modèles numériques indiquent que la troncature du disque se fait au niveau de 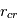$r_{cr}$ sur une échelle de quelques millions d’années, tandis que la dispersion qui s’en suit est beaucoup plus rapide, quelques 10⁵ ans peut-être.