Comprendre
Auteur: Philippe Thébault
- Datation Radio-Isotopique
- Datation radio-isotopique: Principe
- Datation absolue
- Datation relative
- La barrière du mètre
- Dynamique d'un disque de planétésimaux
- Accrétion «Boule de neige»
- Photo-évaporation et dispersion du gaz
Datation Radio-Isotopique
Datation radio-isotopique: Principe
Certains noyaux atomiques, appelés radioisotopes, sont naturellement instables et peuvent spontanément se désintégrer en noyaux moins massifs et stables, libérant de l’énergie sous forme de rayonnement. La décroissance du nombre 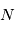 d’un type de radioisotopes
d’un type de radioisotopes 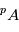 en un élément
en un élément 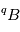 suit une décroissance exponentielle
suit une décroissance exponentielle 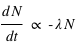 . Où la quantité
. Où la quantité 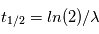 est le temps de demi-vie caractéristique de l’élément. Dans le cas le plus simple où aucun élément
est le temps de demi-vie caractéristique de l’élément. Dans le cas le plus simple où aucun élément 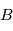 n’est présent initialement le temps t peut être trouvé directement par le rapport
n’est présent initialement le temps t peut être trouvé directement par le rapport 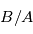 . Mais en réalité les choses ne sont jamais aussi simples, et ce pour au moins 2 raisons :
. Mais en réalité les choses ne sont jamais aussi simples, et ce pour au moins 2 raisons :
1) Il y a a priori toujours du 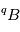 présent à
présent à 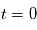 ou, du moins, il est impossible d’exclure cette présence. Et on ne connait pas a priori cette quantité initiale de
ou, du moins, il est impossible d’exclure cette présence. Et on ne connait pas a priori cette quantité initiale de 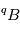
2) l’isotope 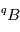 n’est souvent pas le seul possible pour l’élément
n’est souvent pas le seul possible pour l’élément 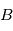 , qui peut également exister sous la forme
, qui peut également exister sous la forme 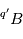 , ce qui peut fortement compliquer les choses. En effet, dans un matériau à l'état gazeux ou liquide, les isotopes
, ce qui peut fortement compliquer les choses. En effet, dans un matériau à l'état gazeux ou liquide, les isotopes 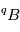 et
et 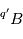 vont naturellement s'équilibrer entre eux à une valeur d'équilibre. En conséquence, dès qu'un matériau fond ou fusionne, toute information sur la quantité d'isotope
vont naturellement s'équilibrer entre eux à une valeur d'équilibre. En conséquence, dès qu'un matériau fond ou fusionne, toute information sur la quantité d'isotope 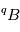 produite par désintégration de
produite par désintégration de 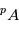 va être perdue par cette mise à l'équilibre isotopique (autrement dit, toute fusion est un "reset" des isotopes de B).
va être perdue par cette mise à l'équilibre isotopique (autrement dit, toute fusion est un "reset" des isotopes de B).
Ceci va rendre la datation plus compliquée, mais elle reste néanmoins possible, du moins pour remonter jusqu'au moment de la dernière condensation du matériau. On peut grosso-modo distinguer 2 types de datation : datation absolue et datation relative.
Datation absolue
La désintégration de 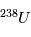 en
en 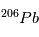 a un temps de ½ vie de 4.47 109 ans, idéal pour mesurer l’âge des plus anciens corps du système solaire. Mais
a un temps de ½ vie de 4.47 109 ans, idéal pour mesurer l’âge des plus anciens corps du système solaire. Mais 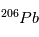 n’est pas l’isotope naturel du
n’est pas l’isotope naturel du 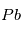 , qui est
, qui est 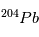 . On obtient alors la relation suivante, liant les abondances de
. On obtient alors la relation suivante, liant les abondances de 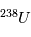 ,
, 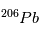 et
et 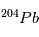 :
:
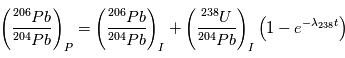
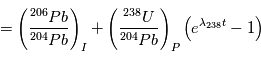
où les indices 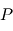 et
et 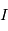 se réfèrent aux abondances actuelles et initiales, respectivement. Le moment "initial" correspond à l'instant où l'objet en question s'est solidifié pour la dernière fois. En effet, dès que le corps fond ou se sublime en gaz, les proportions des 2 isotopes
se réfèrent aux abondances actuelles et initiales, respectivement. Le moment "initial" correspond à l'instant où l'objet en question s'est solidifié pour la dernière fois. En effet, dès que le corps fond ou se sublime en gaz, les proportions des 2 isotopes 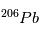 et
et 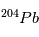 s'équilibrent rapidement à leur proportion "naturelle" et toute information sur la désintégration de
s'équilibrent rapidement à leur proportion "naturelle" et toute information sur la désintégration de 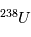 est perdue (voir page précédente ). A cet instant initial le rapport
est perdue (voir page précédente ). A cet instant initial le rapport 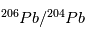 est donc égal à la valeur d'équilibre. En revanche, une fois le corps solidifié, un excès de l'isotope
est donc égal à la valeur d'équilibre. En revanche, une fois le corps solidifié, un excès de l'isotope 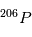 va petit à petit se créer à mesure que
va petit à petit se créer à mesure que 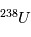 se désintègre. La variable inconnue est ici la quantité initiale absolue de
se désintègre. La variable inconnue est ici la quantité initiale absolue de 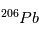 (ou de
(ou de 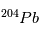 ), que l'on ne connaît pas a priori. Heureusement, il existe un deuxième type de désintégration d’U en Pb, la réaction
), que l'on ne connaît pas a priori. Heureusement, il existe un deuxième type de désintégration d’U en Pb, la réaction 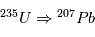 , dont le temps de vie est de 704 106 ans, et qui va nous permettre de contraindre les abondances initiales. Les équations sont alors:
, dont le temps de vie est de 704 106 ans, et qui va nous permettre de contraindre les abondances initiales. Les équations sont alors:
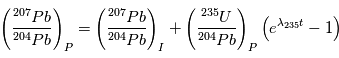
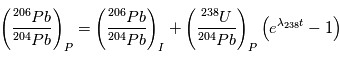
Et donc:
![F = \left [\frac{\left (\frac{{}^{207}Pb}{{}^{204}Pb} \right )_P -\left (\frac{{}^{207}Pb}{{}^{204}Pb} \right )_I }{ \left (\frac{{}^{206}Pb}{{}^{204}Pb} \right )_P - \left (\frac{{}^{206}Pb}{{}^{204}Pb} \right )_I} \right ]=\left ( \frac{1}{137.88} \right )\left ( \frac{e^{\lambda {}_{235}t} -1}{e^{\lambda {}_{238}t} -1} \right )](../pages_mecanique-formation/equations_datation-radio-isotopique/equation41.png)
où 137.88 est la valeur présente de 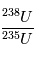 , qui est une constante globale du système solaire actuel, et
, qui est une constante globale du système solaire actuel, et 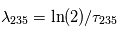 ,
, 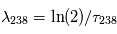 . Cette relation est directement exploitable pour toute météorite non-homogène initialement, mais dont tous les composants se sont formés à la même époque. En effet, dans ce cas, les rapports initiaux
. Cette relation est directement exploitable pour toute météorite non-homogène initialement, mais dont tous les composants se sont formés à la même époque. En effet, dans ce cas, les rapports initiaux 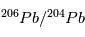 et
et 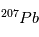 /
/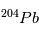 sont les mêmes partout dans la météorite et sont égaux à leurs valeurs d'équilibre (indiquées par a0 et b0 sur la figure). Par conséquent, dans un graphe
sont les mêmes partout dans la météorite et sont égaux à leurs valeurs d'équilibre (indiquées par a0 et b0 sur la figure). Par conséquent, dans un graphe 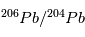 vs.
vs. 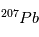 /
/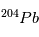 , toutes les mesures du rapport F doivent se situer une même droite, appelée isochrone, dont la pente va directement donner l’âge de la météorite (cf. Figure).
, toutes les mesures du rapport F doivent se situer une même droite, appelée isochrone, dont la pente va directement donner l’âge de la météorite (cf. Figure).
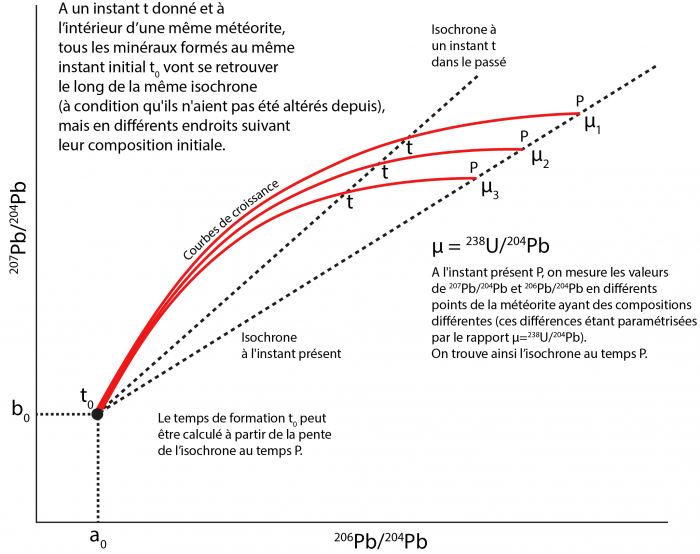
Isochrone isotopique construite à partir des abondances actuelles relatives de 207Pb, 206Pb et 204Pb en différents endroits d’une même météorite
Crédit :
Observatoire de Paris
Datation relative
La désintégration radioactive permet également de dater des corps même bien après la disparition des radionucléotides concernés (c'est à dire bien au delà du temps de 1/2-vie de la désintégration concernée). C’est le cas par exemple de la désintégration 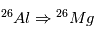 , dont le temps de ½ vie est de « seulement » 720 000ans. Notons que ni
, dont le temps de ½ vie est de « seulement » 720 000ans. Notons que ni 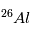 , ni
, ni 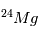 ne sont des isotopes naturels de leurs éléments, qui sont, respectivement,
ne sont des isotopes naturels de leurs éléments, qui sont, respectivement, 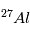 et
et 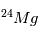 . A la différence de la désintégration d’
. A la différence de la désintégration d’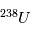 , il n’existe aujourd’hui plus de
, il n’existe aujourd’hui plus de 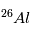 que l’on puisse mesurer. En principe, on a donc :
que l’on puisse mesurer. En principe, on a donc :
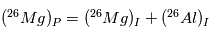
Cette équation n’est pas d’une grande aide en elle-même, mais, comme pour la datation absolue, on peut tirer parti de la non-homogénéité d’une météorite donnée. Si en effet deux endroits de cette météorite avaient initialement des teneurs totales en 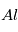 (tous isotopes confondus) différentes, mais que la proportion de
(tous isotopes confondus) différentes, mais que la proportion de 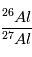 était, elle, la même, alors l’excès de
était, elle, la même, alors l’excès de 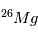 ne sera aujourd’hui pas partout le même, et cet excès sera relié à l’abondance actuelle locale de
ne sera aujourd’hui pas partout le même, et cet excès sera relié à l’abondance actuelle locale de 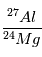 par la relation :
par la relation :
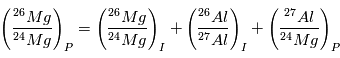
Les mesures de 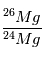 et
et 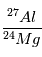 en différents endroits de la météorite
vont alors tracer une isochrone dont la pente donnera la teneur initiale en
en différents endroits de la météorite
vont alors tracer une isochrone dont la pente donnera la teneur initiale en
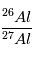 (voir Figure).
(voir Figure).
Maintenant, si on compare les teneurs initiales de 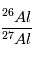 obtenus pour
différentes météorites, on peut obtenir une datation relative des temps de
formation de ces météorites. En effet, étant donné le temps de vie très court
de
obtenus pour
différentes météorites, on peut obtenir une datation relative des temps de
formation de ces météorites. En effet, étant donné le temps de vie très court
de 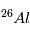 , sa teneur par rapport à
, sa teneur par rapport à 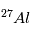 pourra être très différente suivant l’instant
où la météorite s’est formée. Si on compare les valeurs
pourra être très différente suivant l’instant
où la météorite s’est formée. Si on compare les valeurs 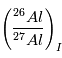 dans 2
météorites différentes, on obtient ainsi la datation relative de leur formation
par la formule:
dans 2
météorites différentes, on obtient ainsi la datation relative de leur formation
par la formule:
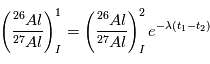
où 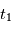 et
et 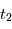 sont les instants de formation des 2 météorites, et
sont les instants de formation des 2 météorites, et 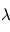 est le taux de
désintégration de la réaction
est le taux de
désintégration de la réaction 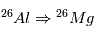
Il faut cependant ici bien faire attention à deux points très importants :
- ces mesures relatives ne sont possibles que si
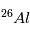 était uniformément
distribué dans la nébuleuse initiale. Les dernières recherches semblent cependant montrer que tel était bien le cas.
était uniformément
distribué dans la nébuleuse initiale. Les dernières recherches semblent cependant montrer que tel était bien le cas. - la fraction de
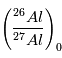 estimée correspond à ce qu’elle était au moment
de la dernière condensation de l’objet. En effet, quand le corps est dans un
état fluide (gaz, liquide), les abondances de
estimée correspond à ce qu’elle était au moment
de la dernière condensation de l’objet. En effet, quand le corps est dans un
état fluide (gaz, liquide), les abondances de 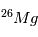 et
et 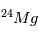 se ré-équilibrent
automatiquement à leurs proportions « naturelles » et tout excès antérieur
de
se ré-équilibrent
automatiquement à leurs proportions « naturelles » et tout excès antérieur
de 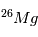 est effacé. Autrement dit, le chronomètre isotopique se « reset » lors
de tout épisode de très forte température.
est effacé. Autrement dit, le chronomètre isotopique se « reset » lors
de tout épisode de très forte température.
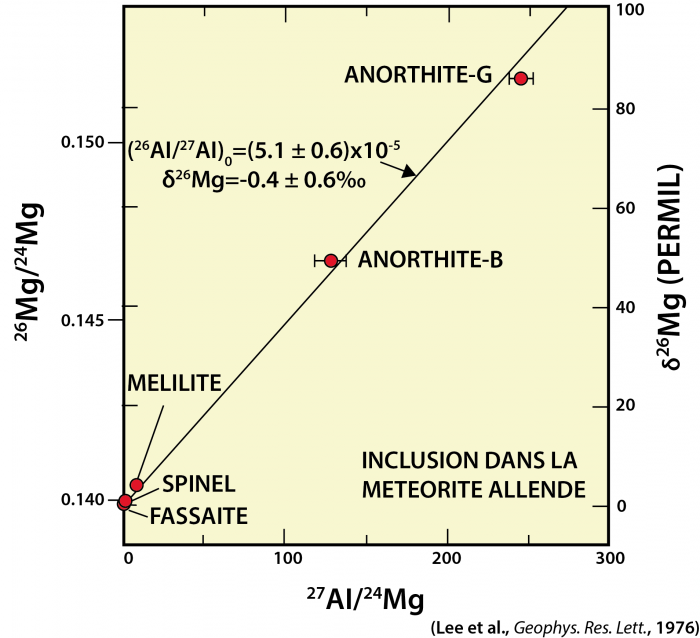
Isochrone obtenue à partir des abondances actuelles des différents isotopes de Mg et Al dans la météorite carbonée « Alliende »
Crédit :
Observatoire de Paris
La barrière du mètre
Comme nous l’avons vu (cf. lien), une des étapes les plus délicates du scénario standard de formation planétaire est celle qui fait passer des premières poussières condensées dans la nébuleuse aux planétésimaux kilométriques. La principale difficulté étant atteinte pour des corps de ∼10cm-1m, pour lesquels les vitesses de collision deviennent trop élevées pour permettre l’accrétion, et qui vont de plus avoir un mouvement de dérive très rapide vers l’étoile centrale. Ces deux problèmes sont tous deux liés à l’action du gaz sur les corps solides. En effet, toute particule solide plongée dans un milieu gazeux subit la friction de ce gaz, qui va être proportionnelle à la surface de contact entre le gaz et l’objet. Cette friction peut ainsi s’exprimer sous la forme
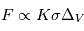
Où 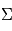 est la section efficace du corps (
est la section efficace du corps (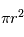 ) et
) et 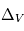 la différence de vitesse entre le gaz et la particule.
Si maintenant on applique le principe fondamental de la dynamique, on obtient que l’accélération
la différence de vitesse entre le gaz et la particule.
Si maintenant on applique le principe fondamental de la dynamique, on obtient que l’accélération 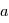 due au gaz vaut:
due au gaz vaut:
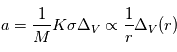
On pourrait a priori se dire que, dans le cas présent, 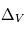 est nul car aussi bien le gaz que les corps solides orbitent autour de l’étoile suivant les mêmes lois de Kepler, et donc en principe à la même vitesse orbitale
est nul car aussi bien le gaz que les corps solides orbitent autour de l’étoile suivant les mêmes lois de Kepler, et donc en principe à la même vitesse orbitale 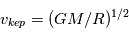 . Mais il y a en fait une différence, car le gaz est lui, en plus, soumis à une force de pression due au gradient de température et de densité dans la nébuleuse. Dans un disque proto-planétaire de type MMSN, cette force de pression s’exerce de l’intérieur vers l’extérieur et tend donc à contrebalancer la gravitation de l’étoile. Tout se passe donc comme si le gaz « percevait » une étoile de masse
. Mais il y a en fait une différence, car le gaz est lui, en plus, soumis à une force de pression due au gradient de température et de densité dans la nébuleuse. Dans un disque proto-planétaire de type MMSN, cette force de pression s’exerce de l’intérieur vers l’extérieur et tend donc à contrebalancer la gravitation de l’étoile. Tout se passe donc comme si le gaz « percevait » une étoile de masse 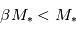 et aura donc une vitesse Képlérienne
et aura donc une vitesse Képlérienne 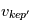 inférieure au
inférieure au 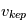 d’un corps solide orbitant dans la vide. On dit alors que le disque de gaz est « sub-Képlérien ».
d’un corps solide orbitant dans la vide. On dit alors que le disque de gaz est « sub-Képlérien ».
Le comportement de corps solides plongés dans ce disque de gaz est alors compris entre 2 extrêmes : les particules les plus petites (<mm) sont piégées dans le gaz et bougent avec lui, et on a dans ce cas 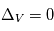 et donc
et donc 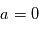 . A l’autre extrême, les planétésimaux très massifs sont, eux, découplés du gaz et subissent de la friction, mais ne vont pas beaucoup en pâtir car le rapport
. A l’autre extrême, les planétésimaux très massifs sont, eux, découplés du gaz et subissent de la friction, mais ne vont pas beaucoup en pâtir car le rapport  est tout petit et ils vont donc être très difficile à bouger par le gaz. Donc la aussi
est tout petit et ils vont donc être très difficile à bouger par le gaz. Donc la aussi 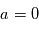 . Entre ces 2 extrêmes, il existe un régime intermédiaire avec des corps suffisamment gros pour être découplés du gaz (
. Entre ces 2 extrêmes, il existe un régime intermédiaire avec des corps suffisamment gros pour être découplés du gaz ( 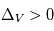 ) mais pas suffisamment massifs pour être insensibles à la friction. Ce régime de taille intermédiaire se situe autour de 10cm-1m. Pour des corps de cette taille l’effet de la friction gazeuse est maximal (cf. image). Et comme
) mais pas suffisamment massifs pour être insensibles à la friction. Ce régime de taille intermédiaire se situe autour de 10cm-1m. Pour des corps de cette taille l’effet de la friction gazeuse est maximal (cf. image). Et comme  , cette friction aura tendance à ralentir les corps solides et à les faire dériver vers l’étoile. Cette vitesse de dérive peut atteindre plus de 50m/s, ce qui correspond à 1UA en moins de 100ans !
, cette friction aura tendance à ralentir les corps solides et à les faire dériver vers l’étoile. Cette vitesse de dérive peut atteindre plus de 50m/s, ce qui correspond à 1UA en moins de 100ans !
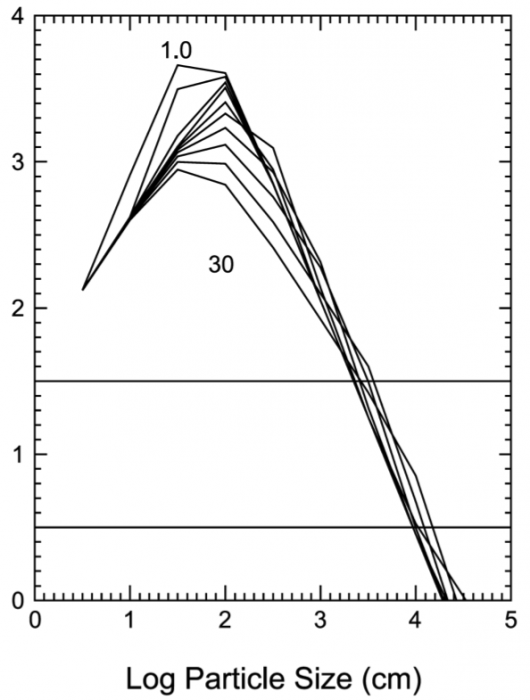
Vitesse de dérive radiale (en cm/s) vers l’étoile centrale, en fonction de taille des corps solides présents dans la nébuleuse protoplanétaire de type MMSN. On voit très clairement qu’un pic est atteint pour des corps proches de la taille du mètre.
Crédit :
Observatoire de Paris
Dynamique d'un disque de planétésimaux
Une population de planétésimaux orbitant le soleil ne pourra former des corps plus massifs que si les vitesses de rencontres mutuelles 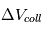 sont, pour une fraction importante de ces rencontres, inférieures à
sont, pour une fraction importante de ces rencontres, inférieures à 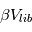 ; où
; où 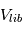 est la vitesse de libération à la surface de 2 planétésimaux en collision et
est la vitesse de libération à la surface de 2 planétésimaux en collision et 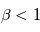 un paramètre prenant en compte la dispersion d’énergie lors de l’impact. Toute la question est alors de savoir si, effectivement, ce critère
un paramètre prenant en compte la dispersion d’énergie lors de l’impact. Toute la question est alors de savoir si, effectivement, ce critère 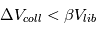 va être rempli dans un disque de planétésimaux kilométriques laissé à lui même.
va être rempli dans un disque de planétésimaux kilométriques laissé à lui même.
L’état dynamique d’un tel disque va dépendre de l’équilibre entre plusieurs mécanismes: la gravité mutuelle des planétésimaux, la force de friction du gaz primordial toujours présent à ce stade, la dissipation d’énergie lors des collisions physiques, et, bien sur, la gravité de l’étoile autour de laquelle tous les corps orbitent. Si on fait l’hypothèse simplificatrice que tous les planétésimaux ont la même taille 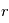 , alors on peut montrer que le disque va tendre vers un état stationnaire où les vitesses de rencontres vont en moyenne être de l’ordre de
, alors on peut montrer que le disque va tendre vers un état stationnaire où les vitesses de rencontres vont en moyenne être de l’ordre de 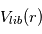 . Si en effet
. Si en effet 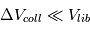 , alors les déflections gravitationnelles lors de rencontres proches vont automatiquement augmenter
, alors les déflections gravitationnelles lors de rencontres proches vont automatiquement augmenter 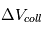 . Et si, à l’inverse,
. Et si, à l’inverse, 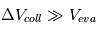 , alors la dissipation d’énergie cinétique lors des collisions va être très forte et fera diminuer
, alors la dissipation d’énergie cinétique lors des collisions va être très forte et fera diminuer 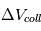 . Cet équilibre autour de
. Cet équilibre autour de 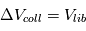 est plutôt une bonne nouvelle, car il entraine qu’une fraction des collisions vont effectivement permettre l’accrétion des corps (sachant qu’il y aura toujours une dispersion des vitesses de collision autour leur valeur moyenne).
est plutôt une bonne nouvelle, car il entraine qu’une fraction des collisions vont effectivement permettre l’accrétion des corps (sachant qu’il y aura toujours une dispersion des vitesses de collision autour leur valeur moyenne).
Sachant que tous ces corps sont en orbite autour d’une étoile, par exemple le Soleil, les vitesses relatives de collisions vont être directement liées à l’excentricité (et à leur inclinaison si on est en 3D) de leurs orbites : plus les orbites sont excentriques, plus 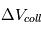 augmente, plus elles sont circulaires, plus
augmente, plus elles sont circulaires, plus 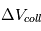 tend vers zero. Pour de petites excentricités, à l’ordre zero on peut écrire que
tend vers zero. Pour de petites excentricités, à l’ordre zero on peut écrire que
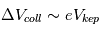
Il faut réaliser que, pour des planétésimaux kilométriques, on a affaire à des vitesses très faibles, car les 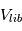 de tels corps sont de l’ordre de quelques mètres par seconde seulement. Ceci se traduit par des excentricités orbitales très faibles, de l’ordre de 0.0001 ! (cf. exercice).
de tels corps sont de l’ordre de quelques mètres par seconde seulement. Ceci se traduit par des excentricités orbitales très faibles, de l’ordre de 0.0001 ! (cf. exercice).
Accrétion «Boule de neige»
Si tous les planétésimaux du disque avaient exactement la même taille r et grandissaient tous à la même vitesse, alors leur taux de croissance serait égal à 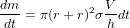 où
où 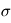 est la densité surfacique de planétésimaux,
est la densité surfacique de planétésimaux, 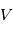 leur vitesse relative de collision et
leur vitesse relative de collision et 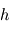 l’épaisseur du disque. Si on fait l’approximation raisonnable que
l’épaisseur du disque. Si on fait l’approximation raisonnable que 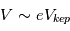 (cf. page précédente) et que
(cf. page précédente) et que 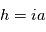 (
(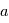 , distance à l’étoile et
, distance à l’étoile et 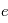 excentricité moyenne de l’orbite des planétésimaux), alors on obtient
excentricité moyenne de l’orbite des planétésimaux), alors on obtient
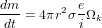 avec
avec 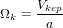 , vitesse angulaire Keplerienne. On trouve alors que
, vitesse angulaire Keplerienne. On trouve alors que 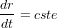 , et que la croissance en taille est linéaire avec le temps. Pour une MMSN à 1UA on trouve qu’il faut alors quelques 106 ans pour former un corps de 1000km (cf. EXERCICE)
, et que la croissance en taille est linéaire avec le temps. Pour une MMSN à 1UA on trouve qu’il faut alors quelques 106 ans pour former un corps de 1000km (cf. EXERCICE)
Mais il semble qu’en réalité l’accrétion suive un chemin beaucoup plus rapide et efficace, mais très sélectif, appelé accrétion « boule de neige ». Il est en effet plus que probable que, dans tout disque réel, toutes les tailles ne sont pas identiques et que, localement, certains planétésimaux soient, par hasard, légèrement plus grands (de taille 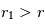 ) que ceux qui les entourent. De ce fait, ils ont une vitesse de libération
) que ceux qui les entourent. De ce fait, ils ont une vitesse de libération 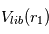 supérieure à celle des corps environnants. En conséquence, ils vont légèrement infléchir la trajectoire des autres corps vers eux. On peut paramétriser cette déflection en considérant que le corps
supérieure à celle des corps environnants. En conséquence, ils vont légèrement infléchir la trajectoire des autres corps vers eux. On peut paramétriser cette déflection en considérant que le corps 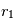 a une section efficace « effective »
a une section efficace « effective » 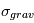 plus grande que sa simple section efficace géométrique
plus grande que sa simple section efficace géométrique 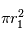 . On a alors
. On a alors
![\Sigma = \pi (r_1+r)^2 \left [ 1+ \left (\frac{V_{lib}(r_1,r)}{\Delta V} \right )^ 2\right ]](../pages_mecanique-formation/equations_formation-comprendre/equation130.png)
Où 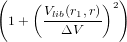 est appelé le terme de « focalisation gravitationnelle ». Du fait de cette surface efficace« dilatée », le corps
est appelé le terme de « focalisation gravitationnelle ». Du fait de cette surface efficace« dilatée », le corps 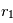 va croître plus vite que les autres. Le rapport
va croître plus vite que les autres. Le rapport 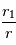 va donc augmenter, ce qui a pour effet d’encore augmenter la focalisation gravitationnelle, et donc le taux de croissance de
va donc augmenter, ce qui a pour effet d’encore augmenter la focalisation gravitationnelle, et donc le taux de croissance de 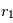 , et ainsi de suite. La croissance de ce corps initialement légèrement privilégié va donc rapidement s’emballer.
, et ainsi de suite. La croissance de ce corps initialement légèrement privilégié va donc rapidement s’emballer.
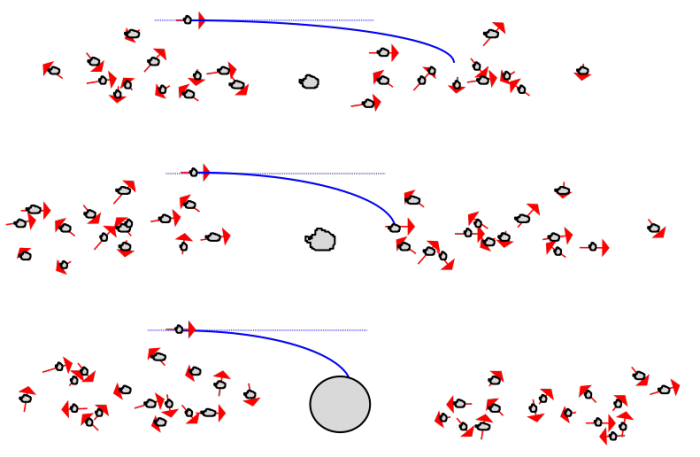
Accrétion boule de neige : un corps initialement plus gros que les planétésimaux qui l‘entourent va légèrement infléchir la trajectoire de ceux-ci vers lui (Figure A). De ce fait, il va croître plus rapidement que les corps qui l’entourent, ce qui va encore accentuer sa tendance à infléchir vers lui l’orbite de ceux-ci (Figure B). Le processus s’auto-amplifie de lui même et conduit à la formation rapide d’un embryon planétaire alors que la majorité des autres planétésimaux n’a pas accrété de matière (Figure C).
Crédit :
Philippe Thebault
Photo-évaporation et dispersion du gaz
L’un des moyens les plus efficaces pour disperser le disque de gaz en moins de 10 millions d’années (voir la page de cours) est le couplage entre (l'accrétion visqueuse du disque) et la photo-évaporation du gaz. Ce dernier mécanisme est la conséquence de l’effet du rayonnement ultra-violet (UV) de l’étoile sur les molécules de gaz, essentiellement 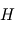 et
et 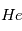 . L’interaction des photons UV va en effet chauffer le gaz, c’est à dire lui donner une plus grande agitation thermique, et si cette vitesse d’agitation thermique dépasse la vitesse Képlerienne locale, alors le gaz est éjecté. Comme
. L’interaction des photons UV va en effet chauffer le gaz, c’est à dire lui donner une plus grande agitation thermique, et si cette vitesse d’agitation thermique dépasse la vitesse Képlerienne locale, alors le gaz est éjecté. Comme 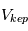 est
est 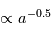 mais que l’énergie transportée par un photon UV ne diminue pas avec la distance à l’étoile, ce sont les molécules des régions extérieures qui seront le plus facilement éjectées lors d’interaction photon-gaz (mais le flux de photon, et donc le taux d’interaction avec le gaz, va, lui, diminuer avec
mais que l’énergie transportée par un photon UV ne diminue pas avec la distance à l’étoile, ce sont les molécules des régions extérieures qui seront le plus facilement éjectées lors d’interaction photon-gaz (mais le flux de photon, et donc le taux d’interaction avec le gaz, va, lui, diminuer avec 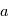 ). On peut ainsi calculer qu’il existe un rayon critique, appelée
). On peut ainsi calculer qu’il existe un rayon critique, appelée 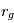 , au delà duquel l’énergie déposée par photo-évaporation dépasse l’énergie orbitale :
, au delà duquel l’énergie déposée par photo-évaporation dépasse l’énergie orbitale :
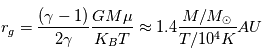
Où 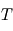 est la température du gaz par suite de l’interaction avec un photon,
est la température du gaz par suite de l’interaction avec un photon, 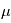 est le poids atomique moyen du gaz,
est le poids atomique moyen du gaz,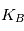 la constante de Boltzman,
la constante de Boltzman, 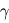 le ratio des chaleurs spécifiques (5/3 pour un gaz mono-atomique),
le ratio des chaleurs spécifiques (5/3 pour un gaz mono-atomique), 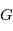 la constante gravitationnelle et
la constante gravitationnelle et 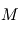 la masse de l’étoile. Dans les faits, à cause de la rotation du gaz, le rayon critique de dispersion est plutôt égal à
la masse de l’étoile. Dans les faits, à cause de la rotation du gaz, le rayon critique de dispersion est plutôt égal à 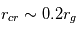 . Pour un rayonnement UV typique, on a
. Pour un rayonnement UV typique, on a 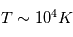 . Pour une étoile de type solaire et un disque de type MMSN , on obtient alors
. Pour une étoile de type solaire et un disque de type MMSN , on obtient alors 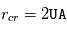 .
.
Cependant, tant que le disque est très dense, à la distance 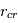 le flux de matière
le flux de matière 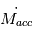 vers l’intérieur du disque dû à la viscosité est supérieur au flux de matière
vers l’intérieur du disque dû à la viscosité est supérieur au flux de matière 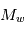 éjecté par photo-évaporation (cf. IMAGE, CASE 1). Mais à mesure que la masse du disque diminue par accrétion sur l’étoile,
éjecté par photo-évaporation (cf. IMAGE, CASE 1). Mais à mesure que la masse du disque diminue par accrétion sur l’étoile, 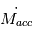 va décroître, jusqu’à ce qu’on atteigne le point où
va décroître, jusqu’à ce qu’on atteigne le point où 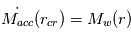 . A partir de ce moment, la matière gazeuse au-delà de
. A partir de ce moment, la matière gazeuse au-delà de 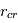 est éjectée du système avant de pouvoir franchir la frontière
est éjectée du système avant de pouvoir franchir la frontière 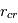 pour se mettre « à l’abri ». Une ouverture est alors créée dans le disque, qui se retrouve coupé en deux. La partie interne du disque est protégée de la photo-évaporation, mais est tellement petite (<2UA) qu’elle va très rapidement être accrétée sur l’étoile (alors qu’auparavant le flux de matière spirallant sur l’étoile était compensé par de la matière venant de plus loin dans le disque). La partie externe du disque va elle se disperser progressivement de l’intérieur (
pour se mettre « à l’abri ». Une ouverture est alors créée dans le disque, qui se retrouve coupé en deux. La partie interne du disque est protégée de la photo-évaporation, mais est tellement petite (<2UA) qu’elle va très rapidement être accrétée sur l’étoile (alors qu’auparavant le flux de matière spirallant sur l’étoile était compensé par de la matière venant de plus loin dans le disque). La partie externe du disque va elle se disperser progressivement de l’intérieur (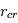 ) vers l’extérieur. Les modèles numériques indiquent que la troncature du disque se fait au niveau de
) vers l’extérieur. Les modèles numériques indiquent que la troncature du disque se fait au niveau de 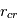 sur une échelle de quelques millions d’années, tandis que la dispersion qui s’en suit est beaucoup plus rapide, quelques 105 ans peut-être.
sur une échelle de quelques millions d’années, tandis que la dispersion qui s’en suit est beaucoup plus rapide, quelques 105 ans peut-être.
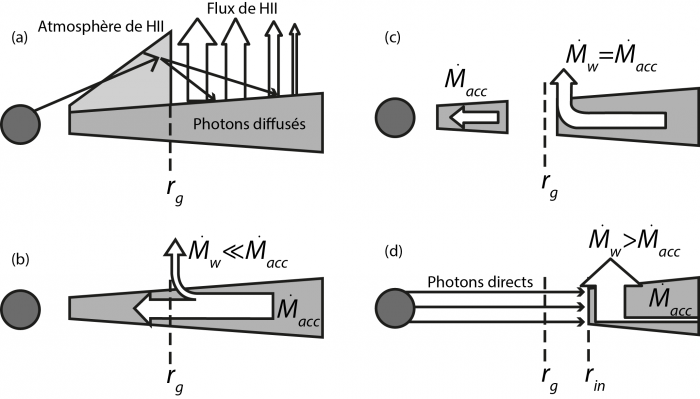
Différentes étapes du processus de dispersion d’un disque proto-planétaire gazeux par photoevaporation et accrétion visqueuse du disque.
Crédit :
Observatoire de Paris
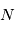 d’un type de radioisotopes
d’un type de radioisotopes 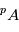 en un élément
en un élément 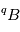 suit une décroissance exponentielle
suit une décroissance exponentielle 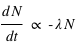 . Où la quantité
. Où la quantité 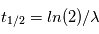 est le temps de demi-vie caractéristique de l’élément. Dans le cas le plus simple où aucun élément
est le temps de demi-vie caractéristique de l’élément. Dans le cas le plus simple où aucun élément 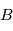 n’est présent initialement le temps t peut être trouvé directement par le rapport
n’est présent initialement le temps t peut être trouvé directement par le rapport 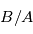 . Mais en réalité les choses ne sont jamais aussi simples, et ce pour au moins 2 raisons :
. Mais en réalité les choses ne sont jamais aussi simples, et ce pour au moins 2 raisons :
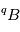 présent à
présent à 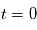 ou, du moins, il est impossible d’exclure cette présence. Et on ne connait pas a priori cette quantité initiale de
ou, du moins, il est impossible d’exclure cette présence. Et on ne connait pas a priori cette quantité initiale de 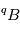
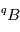 n’est souvent pas le seul possible pour l’élément
n’est souvent pas le seul possible pour l’élément 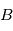 , qui peut également exister sous la forme
, qui peut également exister sous la forme 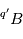 , ce qui peut fortement compliquer les choses. En effet, dans un matériau à l'état gazeux ou liquide, les isotopes
, ce qui peut fortement compliquer les choses. En effet, dans un matériau à l'état gazeux ou liquide, les isotopes 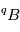 et
et 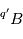 vont naturellement s'équilibrer entre eux à une valeur d'équilibre. En conséquence, dès qu'un matériau fond ou fusionne, toute information sur la quantité d'isotope
vont naturellement s'équilibrer entre eux à une valeur d'équilibre. En conséquence, dès qu'un matériau fond ou fusionne, toute information sur la quantité d'isotope 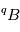 produite par désintégration de
produite par désintégration de 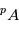 va être perdue par cette mise à l'équilibre isotopique (autrement dit, toute fusion est un "reset" des isotopes de B).
va être perdue par cette mise à l'équilibre isotopique (autrement dit, toute fusion est un "reset" des isotopes de B).
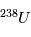 en
en 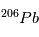 a un temps de ½ vie de 4.47 109 ans, idéal pour mesurer l’âge des plus anciens corps du système solaire. Mais
a un temps de ½ vie de 4.47 109 ans, idéal pour mesurer l’âge des plus anciens corps du système solaire. Mais 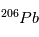 n’est pas l’isotope naturel du
n’est pas l’isotope naturel du 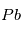 , qui est
, qui est 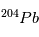 . On obtient alors la relation suivante, liant les abondances de
. On obtient alors la relation suivante, liant les abondances de 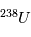 ,
, 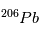 et
et 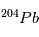 :
:
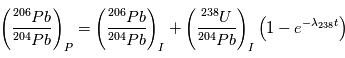
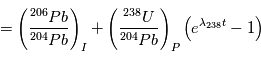
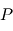 et
et 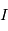 se réfèrent aux abondances actuelles et initiales, respectivement. Le moment "initial" correspond à l'instant où l'objet en question s'est solidifié pour la dernière fois. En effet, dès que le corps fond ou se sublime en gaz, les proportions des 2 isotopes
se réfèrent aux abondances actuelles et initiales, respectivement. Le moment "initial" correspond à l'instant où l'objet en question s'est solidifié pour la dernière fois. En effet, dès que le corps fond ou se sublime en gaz, les proportions des 2 isotopes 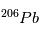 et
et 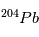 s'équilibrent rapidement à leur proportion "naturelle" et toute information sur la désintégration de
s'équilibrent rapidement à leur proportion "naturelle" et toute information sur la désintégration de 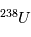 est perdue (voir
est perdue (voir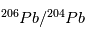 est donc égal à la valeur d'équilibre. En revanche, une fois le corps solidifié, un excès de l'isotope
est donc égal à la valeur d'équilibre. En revanche, une fois le corps solidifié, un excès de l'isotope 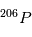 va petit à petit se créer à mesure que
va petit à petit se créer à mesure que 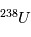 se désintègre. La variable inconnue est ici la quantité initiale absolue de
se désintègre. La variable inconnue est ici la quantité initiale absolue de 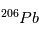 (ou de
(ou de 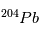 ), que l'on ne connaît pas a priori. Heureusement, il existe un deuxième type de désintégration d’U en Pb, la réaction
), que l'on ne connaît pas a priori. Heureusement, il existe un deuxième type de désintégration d’U en Pb, la réaction 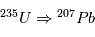 , dont le temps de vie est de 704 106 ans, et qui va nous permettre de contraindre les abondances initiales. Les équations sont alors:
, dont le temps de vie est de 704 106 ans, et qui va nous permettre de contraindre les abondances initiales. Les équations sont alors:
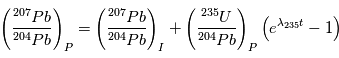
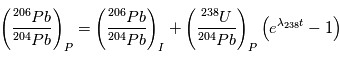
![F = \left [\frac{\left (\frac{{}^{207}Pb}{{}^{204}Pb} \right )_P -\left (\frac{{}^{207}Pb}{{}^{204}Pb} \right )_I }{ \left (\frac{{}^{206}Pb}{{}^{204}Pb} \right )_P - \left (\frac{{}^{206}Pb}{{}^{204}Pb} \right )_I} \right ]=\left ( \frac{1}{137.88} \right )\left ( \frac{e^{\lambda {}_{235}t} -1}{e^{\lambda {}_{238}t} -1} \right )](../pages_mecanique-formation/equations_datation-radio-isotopique/equation41.png)
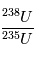 , qui est une constante globale du système solaire actuel, et
, qui est une constante globale du système solaire actuel, et 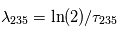 ,
, 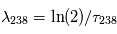 . Cette relation est directement exploitable pour toute météorite non-homogène initialement, mais dont tous les composants se sont formés à la même époque. En effet, dans ce cas, les rapports initiaux
. Cette relation est directement exploitable pour toute météorite non-homogène initialement, mais dont tous les composants se sont formés à la même époque. En effet, dans ce cas, les rapports initiaux 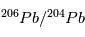 et
et 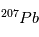 /
/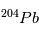 sont les mêmes partout dans la météorite et sont égaux à leurs valeurs d'équilibre (indiquées par a0 et b0 sur la figure). Par conséquent, dans un graphe
sont les mêmes partout dans la météorite et sont égaux à leurs valeurs d'équilibre (indiquées par a0 et b0 sur la figure). Par conséquent, dans un graphe 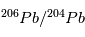 vs.
vs. 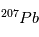 /
/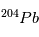 , toutes les mesures du rapport F doivent se situer une même droite, appelée isochrone, dont la pente va directement donner l’âge de la météorite (
, toutes les mesures du rapport F doivent se situer une même droite, appelée isochrone, dont la pente va directement donner l’âge de la météorite (
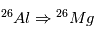 , dont le temps de ½ vie est de « seulement » 720 000ans. Notons que ni
, dont le temps de ½ vie est de « seulement » 720 000ans. Notons que ni 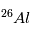 , ni
, ni 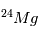 ne sont des isotopes naturels de leurs éléments, qui sont, respectivement,
ne sont des isotopes naturels de leurs éléments, qui sont, respectivement, 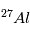 et
et 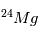 . A la différence de la désintégration d’
. A la différence de la désintégration d’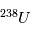 , il n’existe aujourd’hui plus de
, il n’existe aujourd’hui plus de 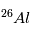 que l’on puisse mesurer. En principe, on a donc :
que l’on puisse mesurer. En principe, on a donc :
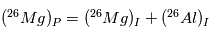
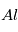 (tous isotopes confondus) différentes, mais que la proportion de
(tous isotopes confondus) différentes, mais que la proportion de 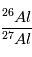 était, elle, la même, alors l’excès de
était, elle, la même, alors l’excès de 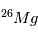 ne sera aujourd’hui pas partout le même, et cet excès sera relié à l’abondance actuelle locale de
ne sera aujourd’hui pas partout le même, et cet excès sera relié à l’abondance actuelle locale de 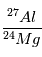 par la relation :
par la relation :
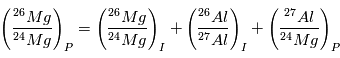
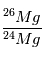 et
et 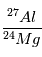 en différents endroits de la météorite
vont alors tracer une isochrone dont la pente donnera la teneur initiale en
en différents endroits de la météorite
vont alors tracer une isochrone dont la pente donnera la teneur initiale en
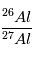 (
(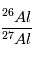 obtenus pour
différentes météorites, on peut obtenir une datation relative des temps de
formation de ces météorites. En effet, étant donné le temps de vie très court
de
obtenus pour
différentes météorites, on peut obtenir une datation relative des temps de
formation de ces météorites. En effet, étant donné le temps de vie très court
de 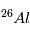 , sa teneur par rapport à
, sa teneur par rapport à 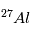 pourra être très différente suivant l’instant
où la météorite s’est formée. Si on compare les valeurs
pourra être très différente suivant l’instant
où la météorite s’est formée. Si on compare les valeurs 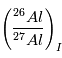 dans 2
météorites différentes, on obtient ainsi la datation relative de leur formation
par la formule:
dans 2
météorites différentes, on obtient ainsi la datation relative de leur formation
par la formule:
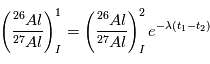
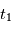 et
et 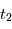 sont les instants de formation des 2 météorites, et
sont les instants de formation des 2 météorites, et 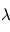 est le taux de
désintégration de la réaction
est le taux de
désintégration de la réaction 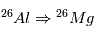
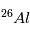 était uniformément
distribué dans la nébuleuse initiale. Les dernières recherches semblent cependant montrer que tel était bien le cas.
était uniformément
distribué dans la nébuleuse initiale. Les dernières recherches semblent cependant montrer que tel était bien le cas. 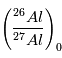 estimée correspond à ce qu’elle était au moment
de la dernière condensation de l’objet. En effet, quand le corps est dans un
état fluide (gaz, liquide), les abondances de
estimée correspond à ce qu’elle était au moment
de la dernière condensation de l’objet. En effet, quand le corps est dans un
état fluide (gaz, liquide), les abondances de 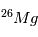 et
et 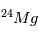 se ré-équilibrent
automatiquement à leurs proportions « naturelles » et tout excès antérieur
de
se ré-équilibrent
automatiquement à leurs proportions « naturelles » et tout excès antérieur
de 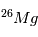 est effacé. Autrement dit, le chronomètre isotopique se « reset » lors
de tout épisode de très forte température.
est effacé. Autrement dit, le chronomètre isotopique se « reset » lors
de tout épisode de très forte température.
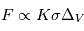
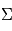 est la section efficace du corps (
est la section efficace du corps (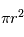 ) et
) et 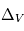 la différence de vitesse entre le gaz et la particule.
Si maintenant on applique le principe fondamental de la dynamique, on obtient que l’accélération
la différence de vitesse entre le gaz et la particule.
Si maintenant on applique le principe fondamental de la dynamique, on obtient que l’accélération 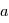 due au gaz vaut:
due au gaz vaut:
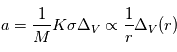
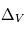 est nul car aussi bien le gaz que les corps solides orbitent autour de l’étoile suivant les mêmes lois de Kepler, et donc en principe à la même vitesse orbitale
est nul car aussi bien le gaz que les corps solides orbitent autour de l’étoile suivant les mêmes lois de Kepler, et donc en principe à la même vitesse orbitale 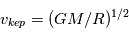 . Mais il y a en fait une différence, car le gaz est lui, en plus, soumis à une force de pression due au gradient de température et de densité dans la nébuleuse. Dans un disque proto-planétaire de type
. Mais il y a en fait une différence, car le gaz est lui, en plus, soumis à une force de pression due au gradient de température et de densité dans la nébuleuse. Dans un disque proto-planétaire de type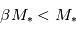 et aura donc une vitesse Képlérienne
et aura donc une vitesse Képlérienne 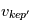 inférieure au
inférieure au 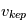 d’un corps solide orbitant dans la vide. On dit alors que le disque de gaz est « sub-Képlérien ».
d’un corps solide orbitant dans la vide. On dit alors que le disque de gaz est « sub-Képlérien ».
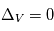 et donc
et donc 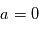 . A l’autre extrême, les planétésimaux très massifs sont, eux, découplés du gaz et subissent de la friction, mais ne vont pas beaucoup en pâtir car le rapport
. A l’autre extrême, les planétésimaux très massifs sont, eux, découplés du gaz et subissent de la friction, mais ne vont pas beaucoup en pâtir car le rapport  est tout petit et ils vont donc être très difficile à bouger par le gaz. Donc la aussi
est tout petit et ils vont donc être très difficile à bouger par le gaz. Donc la aussi 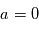 . Entre ces 2 extrêmes, il existe un régime intermédiaire avec des corps suffisamment gros pour être découplés du gaz (
. Entre ces 2 extrêmes, il existe un régime intermédiaire avec des corps suffisamment gros pour être découplés du gaz ( 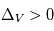 ) mais pas suffisamment massifs pour être insensibles à la friction. Ce régime de taille intermédiaire se situe autour de 10cm-1m. Pour des corps de cette taille l’effet de la friction gazeuse est maximal (
) mais pas suffisamment massifs pour être insensibles à la friction. Ce régime de taille intermédiaire se situe autour de 10cm-1m. Pour des corps de cette taille l’effet de la friction gazeuse est maximal (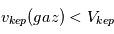 , cette friction aura tendance à ralentir les corps solides et à les faire dériver vers l’étoile. Cette vitesse de dérive peut atteindre plus de 50m/s, ce qui correspond à 1UA en moins de 100ans !
, cette friction aura tendance à ralentir les corps solides et à les faire dériver vers l’étoile. Cette vitesse de dérive peut atteindre plus de 50m/s, ce qui correspond à 1UA en moins de 100ans !

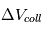 sont, pour une fraction importante de ces rencontres, inférieures à
sont, pour une fraction importante de ces rencontres, inférieures à 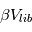 ; où
; où 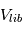 est la vitesse de libération à la surface de 2 planétésimaux en collision et
est la vitesse de libération à la surface de 2 planétésimaux en collision et 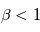 un paramètre prenant en compte la dispersion d’énergie lors de l’impact. Toute la question est alors de savoir si, effectivement, ce critère
un paramètre prenant en compte la dispersion d’énergie lors de l’impact. Toute la question est alors de savoir si, effectivement, ce critère 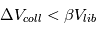 va être rempli dans un disque de planétésimaux kilométriques laissé à lui même.
va être rempli dans un disque de planétésimaux kilométriques laissé à lui même.
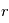 , alors on peut montrer que le disque va tendre vers un état stationnaire où les vitesses de rencontres vont en moyenne être de l’ordre de
, alors on peut montrer que le disque va tendre vers un état stationnaire où les vitesses de rencontres vont en moyenne être de l’ordre de 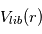 . Si en effet
. Si en effet 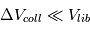 , alors les déflections gravitationnelles lors de rencontres proches vont automatiquement augmenter
, alors les déflections gravitationnelles lors de rencontres proches vont automatiquement augmenter 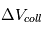 . Et si, à l’inverse,
. Et si, à l’inverse, 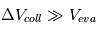 , alors la dissipation d’énergie cinétique lors des collisions va être très forte et fera diminuer
, alors la dissipation d’énergie cinétique lors des collisions va être très forte et fera diminuer 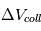 . Cet équilibre autour de
. Cet équilibre autour de 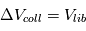 est plutôt une bonne nouvelle, car il entraine qu’une fraction des collisions vont effectivement permettre l’accrétion des corps (sachant qu’il y aura toujours une dispersion des vitesses de collision autour leur valeur moyenne).
est plutôt une bonne nouvelle, car il entraine qu’une fraction des collisions vont effectivement permettre l’accrétion des corps (sachant qu’il y aura toujours une dispersion des vitesses de collision autour leur valeur moyenne).
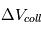 augmente, plus elles sont circulaires, plus
augmente, plus elles sont circulaires, plus 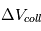 tend vers zero. Pour de petites excentricités, à l’ordre zero on peut écrire que
tend vers zero. Pour de petites excentricités, à l’ordre zero on peut écrire que
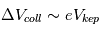
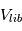 de tels corps sont de l’ordre de quelques mètres par seconde seulement. Ceci se traduit par des excentricités orbitales très faibles, de l’ordre de 0.0001 ! (
de tels corps sont de l’ordre de quelques mètres par seconde seulement. Ceci se traduit par des excentricités orbitales très faibles, de l’ordre de 0.0001 ! (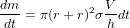 où
où 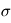 est la densité surfacique de planétésimaux,
est la densité surfacique de planétésimaux, 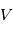 leur vitesse relative de collision et
leur vitesse relative de collision et 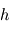 l’épaisseur du disque. Si on fait l’approximation raisonnable que
l’épaisseur du disque. Si on fait l’approximation raisonnable que 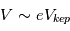 (
(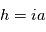 (
(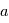 , distance à l’étoile et
, distance à l’étoile et 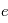 excentricité moyenne de l’orbite des planétésimaux), alors on obtient
excentricité moyenne de l’orbite des planétésimaux), alors on obtient
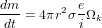 avec
avec 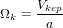 , vitesse angulaire Keplerienne. On trouve alors que
, vitesse angulaire Keplerienne. On trouve alors que 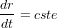 , et que la croissance en taille est linéaire avec le temps. Pour une MMSN à 1UA on trouve qu’il faut alors quelques 106 ans pour former un corps de 1000km (cf.
, et que la croissance en taille est linéaire avec le temps. Pour une MMSN à 1UA on trouve qu’il faut alors quelques 106 ans pour former un corps de 1000km (cf. 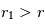 ) que ceux qui les entourent. De ce fait, ils ont une vitesse de libération
) que ceux qui les entourent. De ce fait, ils ont une vitesse de libération 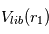 supérieure à celle des corps environnants. En conséquence, ils vont légèrement infléchir la trajectoire des autres corps vers eux. On peut paramétriser cette déflection en considérant que le corps
supérieure à celle des corps environnants. En conséquence, ils vont légèrement infléchir la trajectoire des autres corps vers eux. On peut paramétriser cette déflection en considérant que le corps 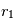 a une section efficace « effective »
a une section efficace « effective » 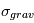 plus grande que sa simple section efficace géométrique
plus grande que sa simple section efficace géométrique 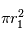 . On a alors
. On a alors
![\Sigma = \pi (r_1+r)^2 \left [ 1+ \left (\frac{V_{lib}(r_1,r)}{\Delta V} \right )^ 2\right ]](../pages_mecanique-formation/equations_formation-comprendre/equation130.png)
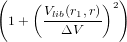 est appelé le terme de « focalisation gravitationnelle ». Du fait de cette surface efficace« dilatée », le corps
est appelé le terme de « focalisation gravitationnelle ». Du fait de cette surface efficace« dilatée », le corps 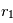 va croître plus vite que les autres. Le rapport
va croître plus vite que les autres. Le rapport 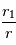 va donc augmenter, ce qui a pour effet d’encore augmenter la focalisation gravitationnelle, et donc le taux de croissance de
va donc augmenter, ce qui a pour effet d’encore augmenter la focalisation gravitationnelle, et donc le taux de croissance de 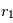 , et ainsi de suite. La croissance de ce corps initialement légèrement privilégié va donc rapidement s’emballer.
, et ainsi de suite. La croissance de ce corps initialement légèrement privilégié va donc rapidement s’emballer.

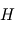 et
et 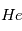 . L’interaction des photons UV va en effet chauffer le gaz, c’est à dire lui donner une plus grande agitation thermique, et si cette vitesse d’agitation thermique dépasse la vitesse Képlerienne locale, alors le gaz est éjecté. Comme
. L’interaction des photons UV va en effet chauffer le gaz, c’est à dire lui donner une plus grande agitation thermique, et si cette vitesse d’agitation thermique dépasse la vitesse Képlerienne locale, alors le gaz est éjecté. Comme 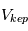 est
est 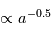 mais que l’énergie transportée par un photon UV ne diminue pas avec la distance à l’étoile, ce sont les molécules des régions extérieures qui seront le plus facilement éjectées lors d’interaction photon-gaz (mais le flux de photon, et donc le taux d’interaction avec le gaz, va, lui, diminuer avec
mais que l’énergie transportée par un photon UV ne diminue pas avec la distance à l’étoile, ce sont les molécules des régions extérieures qui seront le plus facilement éjectées lors d’interaction photon-gaz (mais le flux de photon, et donc le taux d’interaction avec le gaz, va, lui, diminuer avec 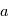 ). On peut ainsi calculer qu’il existe un rayon critique, appelée
). On peut ainsi calculer qu’il existe un rayon critique, appelée 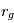 , au delà duquel l’énergie déposée par photo-évaporation dépasse l’énergie orbitale :
, au delà duquel l’énergie déposée par photo-évaporation dépasse l’énergie orbitale :
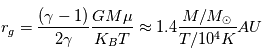
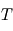 est la température du gaz par suite de l’interaction avec un photon,
est la température du gaz par suite de l’interaction avec un photon, 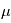 est le poids atomique moyen du gaz,
est le poids atomique moyen du gaz,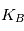 la constante de Boltzman,
la constante de Boltzman, 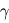 le ratio des chaleurs spécifiques (5/3 pour un gaz mono-atomique),
le ratio des chaleurs spécifiques (5/3 pour un gaz mono-atomique), 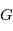 la constante gravitationnelle et
la constante gravitationnelle et 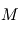 la masse de l’étoile. Dans les faits, à cause de la rotation du gaz, le rayon critique de dispersion est plutôt égal à
la masse de l’étoile. Dans les faits, à cause de la rotation du gaz, le rayon critique de dispersion est plutôt égal à 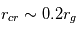 . Pour un rayonnement UV typique, on a
. Pour un rayonnement UV typique, on a 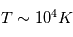 . Pour une étoile de type solaire et un disque de type
. Pour une étoile de type solaire et un disque de type 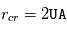 .
.
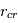 le flux de matière
le flux de matière 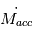 vers l’intérieur du disque dû à la viscosité est supérieur au flux de matière
vers l’intérieur du disque dû à la viscosité est supérieur au flux de matière 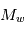 éjecté par photo-évaporation (
éjecté par photo-évaporation (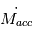 va décroître, jusqu’à ce qu’on atteigne le point où
va décroître, jusqu’à ce qu’on atteigne le point où 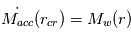 . A partir de ce moment, la matière gazeuse au-delà de
. A partir de ce moment, la matière gazeuse au-delà de 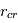 est éjectée du système avant de pouvoir franchir la frontière
est éjectée du système avant de pouvoir franchir la frontière 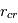 pour se mettre « à l’abri ». Une ouverture est alors créée dans le disque, qui se retrouve coupé en deux. La partie interne du disque est protégée de la photo-évaporation, mais est tellement petite (<2UA) qu’elle va très rapidement être accrétée sur l’étoile (alors qu’auparavant le flux de matière spirallant sur l’étoile était compensé par de la matière venant de plus loin dans le disque). La partie externe du disque va elle se disperser progressivement de l’intérieur (
pour se mettre « à l’abri ». Une ouverture est alors créée dans le disque, qui se retrouve coupé en deux. La partie interne du disque est protégée de la photo-évaporation, mais est tellement petite (<2UA) qu’elle va très rapidement être accrétée sur l’étoile (alors qu’auparavant le flux de matière spirallant sur l’étoile était compensé par de la matière venant de plus loin dans le disque). La partie externe du disque va elle se disperser progressivement de l’intérieur (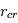 ) vers l’extérieur. Les modèles numériques indiquent que la troncature du disque se fait au niveau de
) vers l’extérieur. Les modèles numériques indiquent que la troncature du disque se fait au niveau de 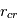 sur une échelle de quelques millions d’années, tandis que la dispersion qui s’en suit est beaucoup plus rapide, quelques 105 ans peut-être.
sur une échelle de quelques millions d’années, tandis que la dispersion qui s’en suit est beaucoup plus rapide, quelques 105 ans peut-être.
