| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Effet Doppler |
On considère une source d'ondes et un observateur. Selon leur vitesse relative, la fréquence reçue par l'observateur varie: c'est ce qu'on appelle l'effet Doppler. Dans le cadre de la physique classique et d'une onde harmonique (purement sinusoidale), on peut le calculer simplement. En effet, notons 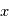 la distance entre la source et l'observateur,
la distance entre la source et l'observateur, 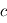 la vitesse de l'onde et. Par définition d'une onde harmonique de pulsation
la vitesse de l'onde et. Par définition d'une onde harmonique de pulsation 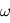 et d'amplitude
et d'amplitude 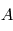 , l'amplitude mesurée à
, l'amplitude mesurée à 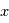 et
et 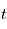 vaut
vaut
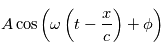
Où 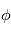 donne en particulier la phase en
donne en particulier la phase en 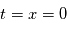 . Si la distance
. Si la distance 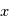 varie avec le temps selon
varie avec le temps selon 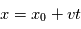 , alors en
, alors en 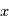 et
et 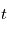 on mesure
on mesure
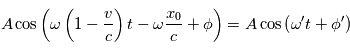
Donc pour l'observateur, tout se passe comme s'il recevait une onde de pulsation 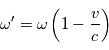 ou de longueur d'onde
ou de longueur d'onde 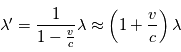 et de phase
et de phase 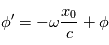 .
.
Cependant, lorsque 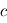 est la vitesse de la lumière, la relativité générale donne une description beaucoup plus précise du phénomène. Nous ne présenterons pas le calcul menant à l'expression de l'effet Doppler dans ce cadre mais en donnons l'expression:
est la vitesse de la lumière, la relativité générale donne une description beaucoup plus précise du phénomène. Nous ne présenterons pas le calcul menant à l'expression de l'effet Doppler dans ce cadre mais en donnons l'expression:
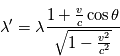
Où 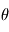 est l'angle entre la direction de la vitesse relative et la ligne de visée observateur-source. Remarquons que lorsque
est l'angle entre la direction de la vitesse relative et la ligne de visée observateur-source. Remarquons que lorsque 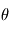 tend vers
tend vers 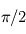 et
et 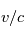 tend vers 0, l'expression tend vers l'expression classique.
tend vers 0, l'expression tend vers l'expression classique.