Instrumentation & Observations
- Objectifs
- Télescope
- CCD
- Bruit de photon
- Exercices
- Effet Doppler
- Spectrographe
- Cross-correlation Function
Objectifs
Jusqu'à présent, on a modélisé la lumière qui parvient à un observateur théorique situé au voisinage de la Terre. Dans cette section, on présentera l'aspect concret de l'observation, en particulier les instruments. En astrométrie on mesure la position sur le detecteur CCD sur le plan focal du télescope, pour les vitesses radiales on utilise un spectrographe dont l'entrée est située au point focal du télescope .
Il est essentiel de bien comprendre le fonctionnement des instruments pour des raisons évidentes: ils constituent notre seule source d'information et leur étude permet de mieux modéliser les mesures, donc d'exploiter au mieux les données.
Dans le cas de l'astrométrie comme celui des vitesses radiales, deux conditions sont nécessaires pour obtenir des mesures suffisamment significatives:
- La quantité de lumière collectée doit être suffisament grande pour obtenir le signal sur bruit désiré
- Les erreurs instrumentales doivent être suffisamment petites pour avoir un rapport signal sur bruit acceptable.
En astrométrie comme en détection par vitesses radiales on place un dispositif sur le plan focal d'un télescope, respectivement des capteurs CCD et l'entrée d'un spectromètre (ou spectrographe). C'est pourquoi les principes généraux des télescopes seront présentés. On évoquera le fonctionnement des spectrographes utilisés pour les détections par mesures de vitesses radiales.
Spectrographe ELODIE

Cet appareil a permis la détection de 51 Pegasi b en 1995 par Michel Mayor et Didier Queloz à l'Observatoire de Haute Provence
Crédit :
Observatoire de Haute Provence
Télescope
Un télescope est un appareil permettant de recueillir un rayonnement eléctromagnétique. Pour observer un rayonneme
nt dans le visible ou dans l'infrarouge proche, on utilise des télescopes à miroir parabolique. Pour éviter les ambiguités, on définira le plan focal comme le plan perpendiculaire à l'axe optique (ici l'axe de symétrie du télescope) passant par le foyer, et on fait l'hypothèse que les rayons reçus font un angle faible avec l'axe optique. Dans ces conditions, La relation donnant la distance au point focal de l'image d'un rayon arrivant avec un angle 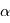 sur le plan focal est en première approximation
sur le plan focal est en première approximation 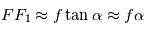 , où
, où 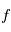 est la distance focale. Pour les angles faibles, on peut travailler avec une lentille équivalente au télescope, de même diamètre et distance focale. On va introduire trois notions de bases sur les télescopes: le champ, la résolution angulaire et la vitesse d'acquisition.
est la distance focale. Pour les angles faibles, on peut travailler avec une lentille équivalente au télescope, de même diamètre et distance focale. On va introduire trois notions de bases sur les télescopes: le champ, la résolution angulaire et la vitesse d'acquisition.
Le champ est la portion du ciel observée par le détecteur du télescope. Comme le détecteur est au plan focal, il est égal à 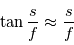
La résolution angulaireest l'angle minimal entre deux sources permettant de les séparer par le système de détection. Cette définition est vague, et Supposons qu'une source ponctuelle émettant à une longueur d'onde 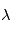 soit placée en un point du plan focal
soit placée en un point du plan focal 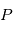 . A cause du phénomène de diffraction, la lumière ne sera pas émise selon une direction unique, mais son énergie sera répartie sur certains angles centrés sur
. A cause du phénomène de diffraction, la lumière ne sera pas émise selon une direction unique, mais son énergie sera répartie sur certains angles centrés sur 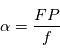 . Comme la lumière suit le même trajet dans les deux sens, ce détecteur reçoit de la lumière provenant de ces angles.
. Comme la lumière suit le même trajet dans les deux sens, ce détecteur reçoit de la lumière provenant de ces angles.
Le rapport du diamètre et de la distance focale du télescope donne la "vitesse" de l'instrument. En effet, considérons une source circulaire de taille angulaire 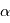 , son image sur le plan focal est un cercle d'aire
, son image sur le plan focal est un cercle d'aire 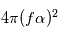 . L'intensité observée est proportionnel à l'aire du télescope, donc l'énergie par unité de temps reçue est proportionnelle à
. L'intensité observée est proportionnel à l'aire du télescope, donc l'énergie par unité de temps reçue est proportionnelle à 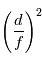 . On définit l'ouverture du télescope par
. On définit l'ouverture du télescope par 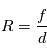 Le rapport signal sur bruit des mesures de CCD est égal à
Le rapport signal sur bruit des mesures de CCD est égal à 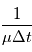 où
où 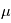 est le nombre moyen d'électron par unité de temps et
est le nombre moyen d'électron par unité de temps et 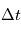 est le temps d'intégration (voir Bruit de photon). On peut calculer le temps d'intégration minimal pour obtenir un certain signal sur bruit compte tenu de l'ouverture du télescope, de la taille de la source et de son intensité. Plus l'aire et grande, plus la distance focale est petite, et plus l'instrument collecte rapidement le nombre de photons requis.
est le temps d'intégration (voir Bruit de photon). On peut calculer le temps d'intégration minimal pour obtenir un certain signal sur bruit compte tenu de l'ouverture du télescope, de la taille de la source et de son intensité. Plus l'aire et grande, plus la distance focale est petite, et plus l'instrument collecte rapidement le nombre de photons requis.
Cependant, lorsque l'ouverture augmente, la résolution angulaire diminue.
Miroir parabolique
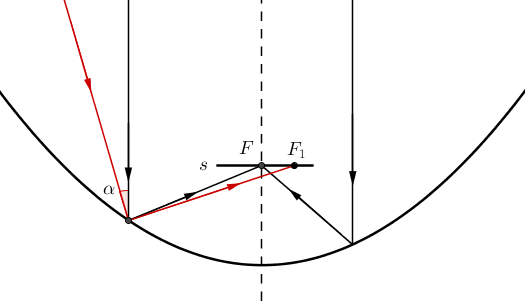
Les rayons perpendiculaires à l'axe de symétrie d'une parabole parviennent au point focal
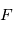
.Ceux qui arrivent avec un certain angle arrivent légèrement décalés.
CCD
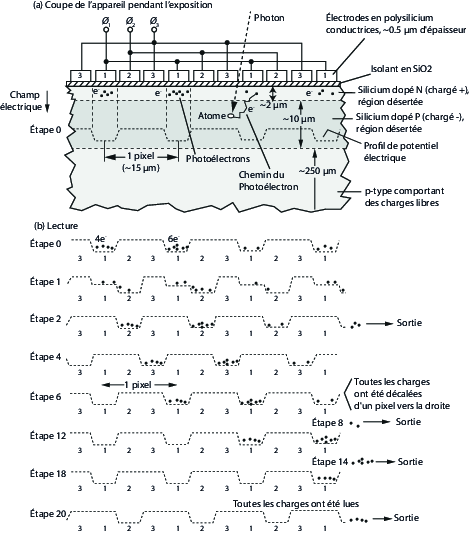
Un détecteur CCD est composé de trois partie: des électrodes en silicium, un isolant en 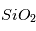 et une jonction de semiconducteurs NP. Les électrodes en polysilicium sont reliées périodoquement par un fil conducteur (toutes les trois électrodes sur la figure) de sorte à créer un profil de potentiel électrique alternant puits et régions plates. Le principe d'un capteur CCD est le suivant (voir figure)
et une jonction de semiconducteurs NP. Les électrodes en polysilicium sont reliées périodoquement par un fil conducteur (toutes les trois électrodes sur la figure) de sorte à créer un profil de potentiel électrique alternant puits et régions plates. Le principe d'un capteur CCD est le suivant (voir figure)
- Lorsqu'un photon percute un atome du slicium dopé N, un électron est émis par effet photo-électrique.
- Une jonction de semi-conducteurs dopés crée un champ électrique (exactement comme dans une diode). Comme la force qui s'exerce sur l'électron est
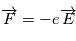 où
où 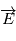 est le champ électrique,
est le champ électrique, 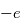 est la charge de l'électron, et que le champ est orienté vers le bas l'électron est piégé sous l'isolant.
est la charge de l'électron, et que le champ est orienté vers le bas l'électron est piégé sous l'isolant. - L'électron est confiné dans un puit de potentiel électrique, selon l'endroit où il a été émis
- Ces trois premières étapes ont lieu pendant tout le temps d'intégration. Ensuite, le nombre d'électron par puit de potentiel est compté, voir (b) sur la figure. Les puits de potentiels sont progressivement décalés et le nombre d'électrons s'y trouvant est compté par puit.
Le contrôle de l'erreur induite par la CCD est primordial et peut s'avérer très complexe. Nous ne rentrerons pas dans ces considérations.
Schéma de principe d'un capteur CCD
Bruit de photon
Exercices
Auteur: Nathan Hara
 Magnitude et temps d'observation
Magnitude et temps d'observation
Difficulté : ☆☆
Effet Doppler
On considère une source d'ondes et un observateur. Selon leur vitesse relative, la fréquence reçue par l'observateur varie: c'est ce qu'on appelle l'effet Doppler. Dans le cadre de la physique classique et d'une onde harmonique (purement sinusoidale), on peut le calculer simplement. En effet, notons 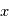 la distance entre la source et l'observateur,
la distance entre la source et l'observateur, 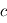 la vitesse de l'onde et. Par définition d'une onde harmonique de pulsation
la vitesse de l'onde et. Par définition d'une onde harmonique de pulsation 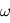 et d'amplitude
et d'amplitude 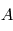 , l'amplitude mesurée à
, l'amplitude mesurée à 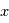 et
et 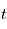 vaut
vaut
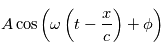
Où 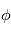 donne en particulier la phase en
donne en particulier la phase en 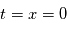 . Si la distance
. Si la distance 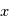 varie avec le temps selon
varie avec le temps selon 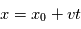 , alors en
, alors en 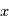 et
et 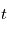 on mesure
on mesure
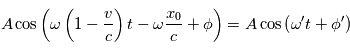
Donc pour l'observateur, tout se passe comme s'il recevait une onde de pulsation 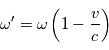 ou de longueur d'onde
ou de longueur d'onde 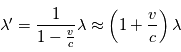 et de phase
et de phase 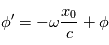 .
.
Cependant, lorsque 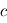 est la vitesse de la lumière, la relativité générale donne une description beaucoup plus précise du phénomène. Nous ne présenterons pas le calcul menant à l'expression de l'effet Doppler dans ce cadre mais en donnons l'expression:
est la vitesse de la lumière, la relativité générale donne une description beaucoup plus précise du phénomène. Nous ne présenterons pas le calcul menant à l'expression de l'effet Doppler dans ce cadre mais en donnons l'expression:
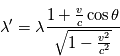
Où 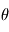 est l'angle entre la direction de la vitesse relative et la ligne de visée observateur-source. Remarquons que lorsque
est l'angle entre la direction de la vitesse relative et la ligne de visée observateur-source. Remarquons que lorsque 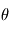 tend vers
tend vers 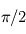 et
et 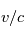 tend vers 0, l'expression tend vers l'expression classique.
tend vers 0, l'expression tend vers l'expression classique.
Spectrographe
L'observation des vitesses radiales nécessite de mesurer des longueurs d'onde très précisément, pour cela on utilise des spectrographe. Les équipes américaines et européennes utilisent des appareils différents, mais dans les deux cas ce sont des spectrographes d'échelle. Le principe d'un tel instrument est d'observer simultanément plusieurs ordres élevés de diffraction à l'aide de deux diffractions successives. La lumière est d'abord diffractée par un premier réseau. Un dispositif, appelé "echelle grating" est placé à un certain angle (blazing angle) du premier réseau de sorte à recevoir des ordres élevés de la première diffraction, qui sont diffractés à nouveau.
Ce dispositif permet "d'étaler" le spectre de sorte qu'une rangée de détecteurs CCD reçoit des longueurs d'ondes très proches, ce qui permet une haute résolution spectrale. En contrepartie, l'énergie est elle aussi répartie, ce qui augmente le temps d'intégration nécessaire pour recevoir suffisamment de lumière pour obtenir un certain rapport signal sur bruit.
D'une mesure à l'autre, à cause de variations internes à l'instrument (température, pression), une longueur d'onde donnée peut se décaler. Comme les mesures doivent pouvoir être comparées entre elles; ce problème doit être résolu efficacement: il faut étalonner l'instrument. Sur ce point, les instruments européens et américains diffèrent. Pour les premiers: ELODIE, CORALIE, HARPS, HARPS-N, l'étalonnage se fait en observant simultanément l'étoile cible est une source dont le spectre est connu. ELODIE observe le ciel, HARPS une lampe thorium-argon calibrée et HARPS-N utilise deux calibrations: un spectre de Fabry-Perot et un "laser frequency comb" (un laser dont le spectre est constitué de raies régulièrement espacées). Les instruments américains font passer la lumière par une cavité contenant de l'iode, dont la position des raies d'absorption est connue. Dans les deux cas on peut comparer Les raies du spectre de référence et celles de l'étoile observée. Si leur déplacement est corrélé (elles se décalent simultanément), il est dû à l'instrument.
La résolution spectrale de ces spectrographes, c'est à dire le rapport 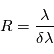 d'une longeur d'onde
d'une longeur d'onde 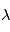 et de la sa variation détectable par le dispositi f
et de la sa variation détectable par le dispositi f 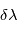 est de l'ordre de 100000. Des simulations numériques (Hatzes & Cochran 1992) ont montré que l'écart type sur la mesure finale de vitesse radiale
est de l'ordre de 100000. Des simulations numériques (Hatzes & Cochran 1992) ont montré que l'écart type sur la mesure finale de vitesse radiale 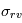 vérifie:
vérifie:
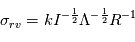
Où 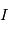 est l'intensité reçue,
est l'intensité reçue, 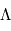 est la plage de fréquences considérées et
est la plage de fréquences considérées et 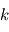 est une constante de proportionnalité. Comme certaines longueurs d'ondes jugées contaminées peuvent être exclues de certaines mesures, cette valeur varie d'une mesure à l'autre.
est une constante de proportionnalité. Comme certaines longueurs d'ondes jugées contaminées peuvent être exclues de certaines mesures, cette valeur varie d'une mesure à l'autre.
Principe du spectrographe d'échelle
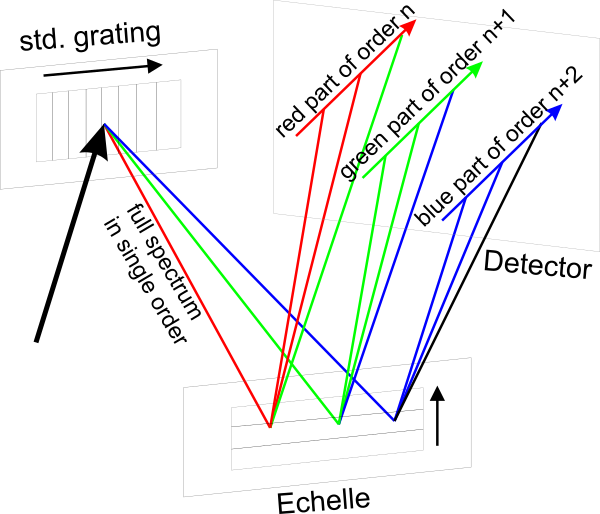
Le rayon incident est d'abord diffracté sur une grille standard (std. grating), puis à nouveau diffracté par le réseau d'échelle. Les trois spectres finalement obtenus sont reçus par des capteurs CCD.
Crédit :
"Echelle Principle" by Boris Považay (Cardiff University) - Own work. Licensed under CC BY-SA 2.5 via Wikimedia Commons
Cross-correlation Function
Réponses aux exercices
pages_ind-vr/exercicebp.html
Exercice
'Magnitude et temps d'observation'

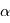 sur le plan focal est en première approximation
sur le plan focal est en première approximation 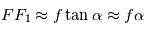 , où
, où 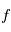 est la distance focale. Pour les angles faibles, on peut travailler avec une lentille équivalente au télescope, de même diamètre et distance focale. On va introduire trois notions de bases sur les télescopes: le champ, la résolution angulaire et la vitesse d'acquisition.
est la distance focale. Pour les angles faibles, on peut travailler avec une lentille équivalente au télescope, de même diamètre et distance focale. On va introduire trois notions de bases sur les télescopes: le champ, la résolution angulaire et la vitesse d'acquisition.
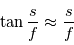
 soit placée en un point du plan focal
soit placée en un point du plan focal 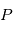 . A cause du phénomène de diffraction, la lumière ne sera pas émise selon une direction unique, mais son énergie sera répartie sur certains angles centrés sur
. A cause du phénomène de diffraction, la lumière ne sera pas émise selon une direction unique, mais son énergie sera répartie sur certains angles centrés sur 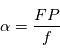 . Comme la lumière suit le même trajet dans les deux sens, ce détecteur reçoit de la lumière provenant de ces angles.
. Comme la lumière suit le même trajet dans les deux sens, ce détecteur reçoit de la lumière provenant de ces angles.
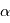 , son image sur le plan focal est un cercle d'aire
, son image sur le plan focal est un cercle d'aire 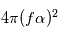 . L'intensité observée est proportionnel à l'aire du télescope, donc l'énergie par unité de temps reçue est proportionnelle à
. L'intensité observée est proportionnel à l'aire du télescope, donc l'énergie par unité de temps reçue est proportionnelle à 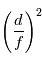 . On définit l'ouverture du télescope par
. On définit l'ouverture du télescope par 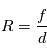 Le rapport signal sur bruit des mesures de CCD est égal à
Le rapport signal sur bruit des mesures de CCD est égal à 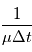 où
où 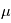 est le nombre moyen d'électron par unité de temps et
est le nombre moyen d'électron par unité de temps et 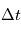 est le temps d'intégration (voir
est le temps d'intégration (voir 
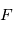 .Ceux qui arrivent avec un certain angle arrivent légèrement décalés.
.Ceux qui arrivent avec un certain angle arrivent légèrement décalés.
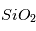 et une jonction de semiconducteurs NP. Les électrodes en polysilicium sont reliées périodoquement par un fil conducteur (toutes les trois électrodes sur la figure) de sorte à créer un profil de potentiel électrique alternant puits et régions plates. Le principe d'un capteur CCD est le suivant (voir figure)
et une jonction de semiconducteurs NP. Les électrodes en polysilicium sont reliées périodoquement par un fil conducteur (toutes les trois électrodes sur la figure) de sorte à créer un profil de potentiel électrique alternant puits et régions plates. Le principe d'un capteur CCD est le suivant (voir figure)
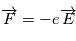 où
où 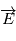 est le champ électrique,
est le champ électrique, 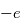 est la charge de l'électron, et que le champ est orienté vers le bas l'électron est piégé sous l'isolant.
est la charge de l'électron, et que le champ est orienté vers le bas l'électron est piégé sous l'isolant. 
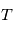 le temps d'attente entre deux émission de photon, la probabilité que
le temps d'attente entre deux émission de photon, la probabilité que 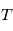 soit supérieure à
soit supérieure à 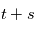 sachant que
sachant que 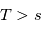 est
est 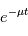 où
où 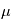 est une constante.
est une constante.
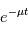 diminue rapidement à
diminue rapidement à 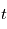 donné, c'est à dire plus la probabilité que
donné, c'est à dire plus la probabilité que 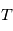 soit long diminue. On peut montrer
soit long diminue. On peut montrer 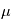 est le nombre d'évènement par unité de temps moyen, proportionnelle à l'intensité. Rappelons que le détecteur capte des photons pendant le
est le nombre d'évènement par unité de temps moyen, proportionnelle à l'intensité. Rappelons que le détecteur capte des photons pendant le 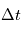 . Le nombre de photons reçus
. Le nombre de photons reçus 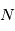 pendant ce temps est une variable aléatoire suivant la loi:
pendant ce temps est une variable aléatoire suivant la loi:
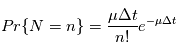
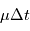 . En conséquence, l'écart-type vaut
. En conséquence, l'écart-type vaut 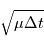 donc le rapport signal sur bruit (Signal-to-Noise Ratio) est:
donc le rapport signal sur bruit (Signal-to-Noise Ratio) est:
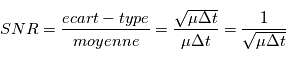
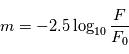 où
où 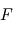 est le flux lumineux reçu et un flux de référence. Le choix de 2.5 et
est le flux lumineux reçu et un flux de référence. Le choix de 2.5 et 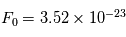 W
W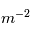
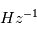 fait que les étoiles de classe 1 d'Hipparque aient une magnitude comprise entre 0 et 1, les classes 2 on une magnitude entre 1 et 2 etc. De ce fait, il semble naturel que les objets les moins lumineux visibles à l'oeil nu soient environ de magnitude 6. On considère un télescope de diamètre
fait que les étoiles de classe 1 d'Hipparque aient une magnitude comprise entre 0 et 1, les classes 2 on une magnitude entre 1 et 2 etc. De ce fait, il semble naturel que les objets les moins lumineux visibles à l'oeil nu soient environ de magnitude 6. On considère un télescope de diamètre 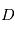 , on suppose qu'on observe dans le visible
, on suppose qu'on observe dans le visible ![\Delta \lambda = [400,800]](../pages_ind-vr/equations_instrumentation/equation42.png) nm, et que le flux lumineux reçu ne dépend pas de la longueur d'onde sur cette plage.
nm, et que le flux lumineux reçu ne dépend pas de la longueur d'onde sur cette plage.
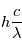 où
où 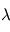 est la longueur d'onde et
est la longueur d'onde et 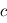 la vitesse de la lumière, montrer que le flux de photon reçus
la vitesse de la lumière, montrer que le flux de photon reçus 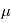 (photons par seconde) est lié au flux
(photons par seconde) est lié au flux 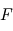 par
par 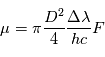
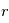 en fonction de la magnitude observée, de
en fonction de la magnitude observée, de 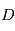 et
et 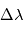
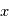 la distance entre la source et l'observateur,
la distance entre la source et l'observateur, 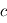 la vitesse de l'onde et. Par définition d'une onde harmonique de pulsation
la vitesse de l'onde et. Par définition d'une onde harmonique de pulsation 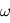 et d'amplitude
et d'amplitude 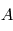 , l'amplitude mesurée à
, l'amplitude mesurée à 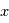 et
et 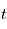 vaut
vaut
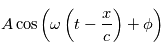
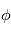 donne en particulier la phase en
donne en particulier la phase en  . Si la distance
. Si la distance 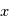 varie avec le temps selon
varie avec le temps selon 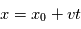 , alors en
, alors en 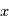 et
et 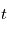 on mesure
on mesure
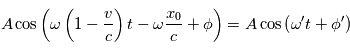
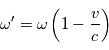 ou de longueur d'onde
ou de longueur d'onde 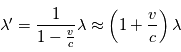 et de phase
et de phase 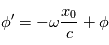 .
.
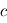 est la vitesse de la lumière, la relativité générale donne une description beaucoup plus précise du phénomène. Nous ne présenterons pas le calcul menant à l'expression de l'effet Doppler dans ce cadre mais en donnons l'expression:
est la vitesse de la lumière, la relativité générale donne une description beaucoup plus précise du phénomène. Nous ne présenterons pas le calcul menant à l'expression de l'effet Doppler dans ce cadre mais en donnons l'expression:
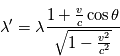
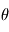 est l'angle entre la direction de la vitesse relative et la ligne de visée observateur-source. Remarquons que lorsque
est l'angle entre la direction de la vitesse relative et la ligne de visée observateur-source. Remarquons que lorsque 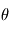 tend vers
tend vers 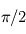 et
et 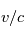 tend vers 0, l'expression tend vers l'expression classique.
tend vers 0, l'expression tend vers l'expression classique.
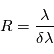 d'une longeur d'onde
d'une longeur d'onde 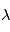 et de la sa variation détectable par le dispositi f
et de la sa variation détectable par le dispositi f 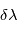 est de l'ordre de 100000. Des simulations numériques (Hatzes & Cochran 1992) ont montré que l'écart type sur la mesure finale de vitesse radiale
est de l'ordre de 100000. Des simulations numériques (Hatzes & Cochran 1992) ont montré que l'écart type sur la mesure finale de vitesse radiale 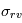 vérifie:
vérifie:
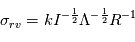
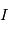 est l'intensité reçue,
est l'intensité reçue, 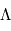 est la plage de fréquences considérées et
est la plage de fréquences considérées et 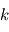 est une constante de proportionnalité. Comme certaines longueurs d'ondes jugées contaminées peuvent être exclues de certaines mesures, cette valeur varie d'une mesure à l'autre.
est une constante de proportionnalité. Comme certaines longueurs d'ondes jugées contaminées peuvent être exclues de certaines mesures, cette valeur varie d'une mesure à l'autre.

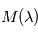 valant 1 pour
valant 1 pour 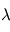 correspondant à une raie d'absorption de l'étoile et 0 ailleurs. Le spectre de l'étoile observée
correspondant à une raie d'absorption de l'étoile et 0 ailleurs. Le spectre de l'étoile observée 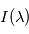 est multiplié par ce masque décalé d'une valeur
est multiplié par ce masque décalé d'une valeur 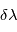 et on mesure
et on mesure 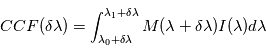 . Où
. Où 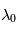 et
et 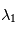 désignent les bornes inférieures et supérieures du spectre observé. Ensuite, une fonction gaussienne
désignent les bornes inférieures et supérieures du spectre observé. Ensuite, une fonction gaussienne 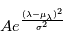 est ajustée sur la CCF. La valeur
est ajustée sur la CCF. La valeur 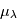 correspondant au minimum de la fonction ajustée est prise comme valeur moyenne du déplacement. L'analyse consiste ensuite à comparer les
correspondant au minimum de la fonction ajustée est prise comme valeur moyenne du déplacement. L'analyse consiste ensuite à comparer les 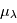 issus d'observations différentes.
issus d'observations différentes.