 |  |  |  |  |  |
| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
| | | | | |
WASP-80 : La planète |
WASP-80 : Les paramètres de la planèteDéduisez maintenant le rayon de la planète et son demi-grand axe.
Il faudra d'abord trouver le rayon de l'étoile WASP-80 afin de pouvoir déterminer le rayon de la planète.
Le calcul du rayon de l'étoile que l'on vient de mener n'est qu'un calcul approximatif etTriaud et al. (2013) sont capable d'estimer ce rayon plus précisément à partir de leur jeu de données, ils trouvent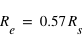 
, que l'on utilisera par la suite pour comparer à leurs résultats.
Maintenant on peut déduire le rayon de la planète. En supposant que l'orbite est circulaire, on peut aussi déduire facilement son rayon orbitale à partir de la 3ème loi de Kepler
On peut maintenant comparer aux valeurs trouvées dans le papier originel de Triaud et al. (2013) (tableau ci-joint).
On voit que nos valeurs pour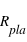 
, la période et le demi-grand axe sont très proches des valeurs originelles.
On peut aussi comparer les valeurs trouvées avec celles de l'encyclopédie exoplanet.eu.
Comme vu dans le cours, on peut faire une première vérification pour tester pour un faux positif, en comparant la durée du transit théorique avec sa durée réelle que l'on a obtenue à la question 3 de la page précédente.
 |  |
, que 
, où 
est la magnitude absolue de l'étoile 
(i.e. la magnitude qu'aurait cette étoile si elle était à 10pc) et enfin que la magnitude absolue 
et la magnitude visuelle, 
sont liées à la distance 
par 
ou 
.
.
et donc 
où l'index 
est pour le Soleil et 
pour l'étoile WASP-80. D'après la définition de la magnitude, on a aussi que 
, où 
est la magnitude absolue de l'étoile. Pour transformer la magnitude mesurée 
(qui dépend de la distance de l'étoile) en magnitude absolue, on utilise 
, soit 
et donc on obtient 
, soit 
.
, on déduit que 
.
.
en supposant un paramètre d'impact nul. On obtient donc une durée de 0.075 jours ou 1.8 heures, ce qui est proche de ce que l'on voit sur le transit zoomé de la page précédente.