 Exercice
Exercice
Nous allons utiliser python pour ce mini-projet. Vous pouvez aussi utiliser votre langage de prédilection si Python ressemble à des hiéroglyphes pour vous.
Commencez par charger le fichier wasp80data.txt qui contient les observations de WASP-80 et faites un graphe représentant la magnitude en fonction du temps, avec les barres d'erreurs associées à chaque point. En python, cela donne :
import numpy as np
import matplotlib.pyplot as plt
bjd, mag, err = np.loadtxt("wasp80data.txt", delimiter=' ', skiprows=1, unpack=True)
plt.errorbar(bjd,mag,err)
On pourrait travailler avec les magnitudes, mais il est plus commun de travailler directement en flux. En effet, un transit produit une baisse du flux total qui provient de l'étoile alors que ça provoque une augmentation de la magnitude et donc on ne verrait pas une baisse mais une croissance de la magnitude lors d'un transit en magnitude. Vous pourrez essayer plus loin de suivre la même procédure en travaillant sur les magnitudes (pour constater que l'on arrive aux mêmes résultats) mais pour le moment on travaillera en flux.
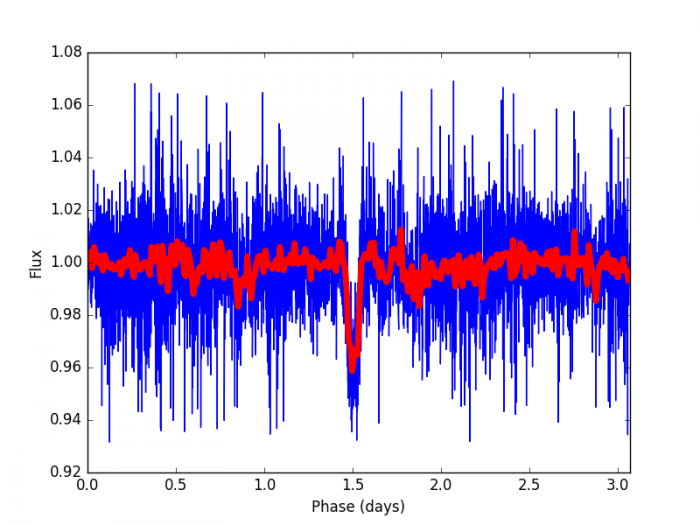
Reproduire le même graphique que précédemment en unité de flux
Que voyons-nous ? Est-ce ce à quoi l'on s'attend ? Voyons-nous un transit ? Pas vraiment ! Ça ne ressemble pas exactement aux courbes théoriques que l'on a vues dans le cours avec une belle chute de flux quand la planète passe devant son étoile. Pour cela il va falloir travailler un peu les données.
Un œil averti se rendra compte que ces données on été pré-traitées. On voit que la magnitude oscille autour de zéro, la composante de magnitude due à l'étoile a donc été retirée. On voit aussi que les données semblent suivre une ligne horizontale, sans qu'il y ait de variations linéaires ou polynomiales. En réalité, quand on obtient les données brutes, c'est beaucoup moins propre que cela, et il faut retirer les effets qui ne sont pas dûs au transit mais plutôt à l'observation en tant que telle. Il peut y avoir des déviations du signal dues à l'instrumentation (par exemple à cause de variations thermiques), ou même des variations de l’atmosphère au cours de l'observation. Il y a différentes méthodes pour réajuster les données afin de corriger ces variations qui ne sont pas dues au transit. De manière générale et simplifiée, cela revient à trouver une fonction polynomiale qui suit au mieux les variations à long terme et de retirer cette fonction du signal. On appelle cela le detrending. Les données que l'on traite ici ont déjà subi ce detrending et peuvent être maintenant exploitées pour chercher un transit potentiel et trouver les paramètres de la planète le cas échéant.
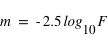
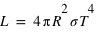 , que
, que 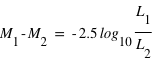 , où
, où 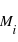 est la magnitude absolue de l'étoile
est la magnitude absolue de l'étoile 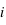 (i.e. la magnitude qu'aurait cette étoile si elle était à 10pc) et enfin que la magnitude absolue
(i.e. la magnitude qu'aurait cette étoile si elle était à 10pc) et enfin que la magnitude absolue 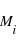 et la magnitude visuelle,
et la magnitude visuelle, 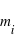 sont liées à la distance
sont liées à la distance 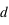 par
par 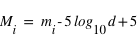
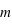 ou
ou 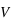 .
.
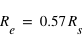 , que l'on utilisera par la suite pour comparer à leurs résultats.
, que l'on utilisera par la suite pour comparer à leurs résultats.
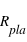 , la période et le demi-grand axe sont très proches des valeurs originelles.
, la période et le demi-grand axe sont très proches des valeurs originelles.

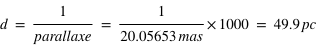 .
.
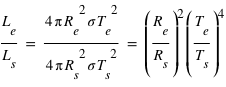 et donc
et donc 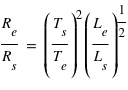 où l'index
où l'index 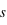 est pour le Soleil et
est pour le Soleil et 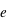 pour l'étoile WASP-80. D'après la définition de la magnitude, on a aussi que
pour l'étoile WASP-80. D'après la définition de la magnitude, on a aussi que 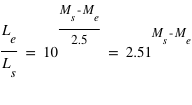 , où
, où 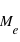 est la magnitude absolue de l'étoile. Pour transformer la magnitude mesurée
est la magnitude absolue de l'étoile. Pour transformer la magnitude mesurée 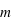 (qui dépend de la distance de l'étoile) en magnitude absolue, on utilise
(qui dépend de la distance de l'étoile) en magnitude absolue, on utilise 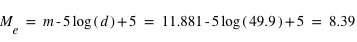 , soit
, soit 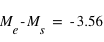 et donc on obtient
et donc on obtient 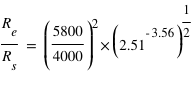 , soit
, soit 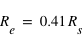 .
.
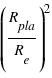 , on déduit que
, on déduit que 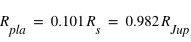 .
.
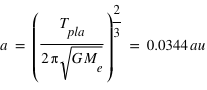 .
.
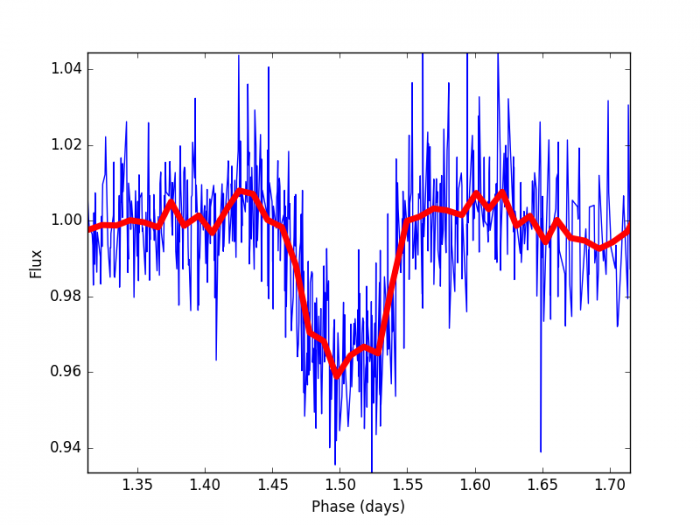
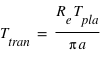 en supposant un paramètre d'impact nul. On obtient donc une durée de 0.075 jours ou 1.8 heures, ce qui est proche de ce que l'on voit sur le transit zoomé de la page précédente.
en supposant un paramètre d'impact nul. On obtient donc une durée de 0.075 jours ou 1.8 heures, ce qui est proche de ce que l'on voit sur le transit zoomé de la page précédente.