| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Température de brillance |
La température de brillance 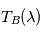 d'un objet est la température du corps noir qui émettrait la même intensité que celle émise par l'objet à la longueur d'onde
d'un objet est la température du corps noir qui émettrait la même intensité que celle émise par l'objet à la longueur d'onde 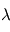 :
: ![I(\lambda) = B\left[\lambda, T_B(\lambda) \right]](../pages_flux-et-spectre/equations_trans-rad/equation33.png) où
où ![B\left[\lambda, T \right]](../pages_flux-et-spectre/equations_trans-rad/equation34.png) désigne la fonction de Planck à la longueur d'onde
désigne la fonction de Planck à la longueur d'onde 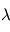 pour un corps noir de température
pour un corps noir de température 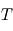 . Comme les courbes représentant les fonctions de Planck ne se croisent jamais, il y a correspondance unique entre
. Comme les courbes représentant les fonctions de Planck ne se croisent jamais, il y a correspondance unique entre 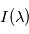 et
et 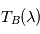 : la température de brillance n'est qu'une autre façon de décrire un spectre. En particulier, elle ne représente pas forcément la température d'un objet physique.
: la température de brillance n'est qu'une autre façon de décrire un spectre. En particulier, elle ne représente pas forcément la température d'un objet physique.
La formule de Planck permet d'exprimer analytiquement 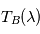 selon la formule
selon la formule 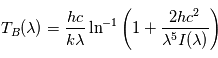 .
.
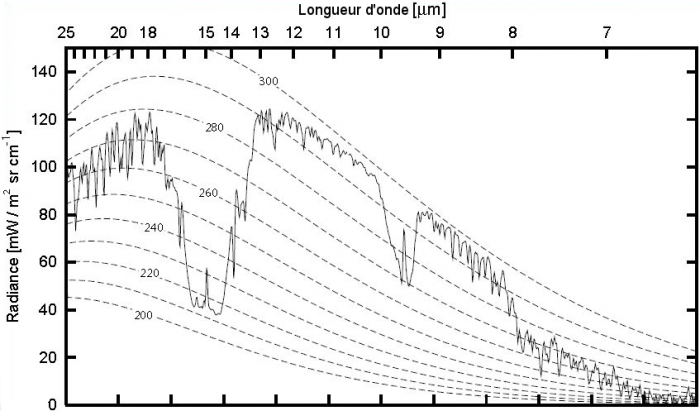
Son intérêt principal réside dans l'interprétation des spectres thermiques issus d'un objet (ici une planète et son atmosphère). En effet, sous réserve de certaines hypothèses :
La température de brillance correspond alors à la température du milieu situé à une profondeur optique égale à 1 : ![T_B(\lambda) \approx T\left[\tau(\lambda) = 1\right]](../pages_flux-et-spectre/equations_trans-rad/equation41.png) avec
avec 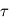 comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :
comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :