Épaisseur optique / Loi de Beer-Lambert

Auteurs: Loïc Rossi, Emmanuel Marcq

Additivité de la profondeur optique

Crédit : Emmanuel Marcq CC-BY-SA

Profondeur optique

On définit alors la transmittance 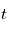comme le rapport entre l'intensité lumineuse 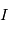après traversée et celle 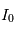I_0 avant la traversée du milieu : 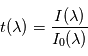$t(\lambda) = \frac{I(\lambda)}{I_0(\lambda)}$ . Cette transmittance vaut 1 si le milieu traversé est transparent, 0 si le milieu est parfaitement opaque, et prend une valeur intermédiaire si le milieu est partiellement opaque. Elle dépend a priori de la longueur d'onde comme la formule l'indique.

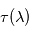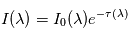La transmittance a l'avantage d'être une grandeur aisément mesurable, mais son interprétation physique directe est malcommode. Il est préférable pour cela d'introduire la grandeur appelée profondeur optique $\tau(\lambda)$ qui se déduit de la transmittance comme suit : $\tau(\lambda) = - \ln \left[ t(\lambda) \right]$ , soit $I(\lambda) = I_0(\lambda) e^{-\tau(\lambda)}$ . Il est alors facile de déduire des propriétés mathématiques du logarithme que 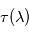$\tau(\lambda)$ est une grandeur additive le long d'un même rayon (voir figure ci-contre), et qu'elle offre donc un paramétrage naturel de l'abscisse curviligne le long de ce rayon. Il est en outre possible de relier physiquement la variation locale de 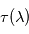$\tau(\lambda)$ le long d'un rayon à la présence de matière traversée : c'est la loi de Beer-Lambert .

Loi de Beer-Lambert

Elle s'exprime comme suit le long d'un rayon lumineux : 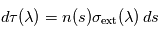$d\tau(\lambda) = n(s) \sigma_{\mathrm{ext}}(\lambda) \, ds$ où 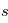désigne l'abscisse curviligne le long du rayon (croissant dans le sens de propagation), 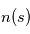n(s) la densité volumique de diffusants et/ou absorbants et 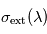$\sigma_{\mathrm{ext}}(\lambda)$ la section efficace d'extinction des diffusants et/ou absorbants. En présence de plusieurs types de diffuseurs et/ou d'absorbeurs, il suffit d'ajouter leurs contributions individuelles. L'évolution de la profondeur optique totale 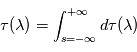$\tau(\lambda) = \int_{s=-\infty}^{+\infty} d\tau(\lambda)$ selon la longueur d'onde au cours d'une occultation ou d'un transit offre donc la possibilité à l'observateur de déduire les propriétés matérielles du milieu traversé (densité volumique et nature physique des particules responsables de l'extinction).