L'interaction entre le rayonnement (ondes du champ électromagnétique) et la matière (chargée au niveau microscopique : électrons, noyaux atomiques) se caractérise par trois types de processus radiatifs : l'absorption, l'émission et la diffusion.
Émission
Un processus d'émission intervient lorsque la matière cède localement de l'énergie au champ électromagnétique (création d'un photon). Cette émission est qualifiée de thermique lorsque le champ et la matière sont à l'équilibre thermodynamique à une même température 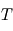 (on peut voir alors leur interaction comme celle d'un gaz de photons perpétuellement absorbés et émis par la matière environnante, et se mettant en équilibre de la sorte). Il existe également des phénomènes d'émission non thermiques (ex: fluorescence, émission laser), mais ils sortent du cadre de ce cours ; certains de ces processus sont vus dans ce chapitre.
(on peut voir alors leur interaction comme celle d'un gaz de photons perpétuellement absorbés et émis par la matière environnante, et se mettant en équilibre de la sorte). Il existe également des phénomènes d'émission non thermiques (ex: fluorescence, émission laser), mais ils sortent du cadre de ce cours ; certains de ces processus sont vus dans ce chapitre.
Illustration d'un processus d'émission spontanée
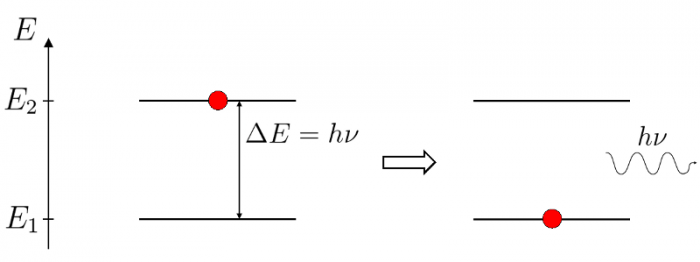
Émission spontanée d'un photon par un système matériel possédant au moins deux niveaux d'énergie. L'énergie totale est conservée dans ce processus.
Absorption
Un processus d'absorption a lieu lorsqu'inversement, le champ électromagnétique cède de l'énergie à la matière environnante (destruction d'un photon).
Illustration d'un processus d'absorption
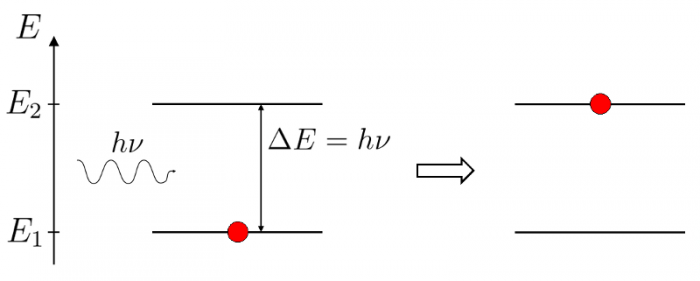
Absorption d'un photon par un système matériel possédant au moins deux niveaux d'énergie. L'énergie totale est conservée dans ce processus.
Diffusion
Lorsque la présence de matière interagit avec l'onde électromagnétique en absorbant et réémettant un photon dans un temps très court, donc sans lui soutirer d'énergie. La réémission s'effectuant dans tout l'espace, il en résulte une déviation des ondes électromagnétiques hors de la direction d'incidence. On appelle ce phénomène diffusion.
Illustration d'un processus de diffusion
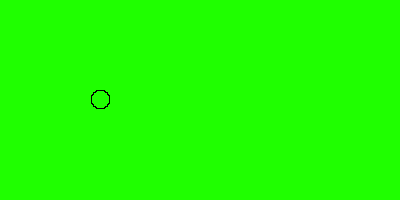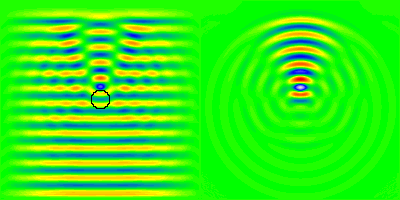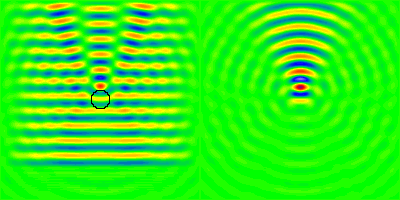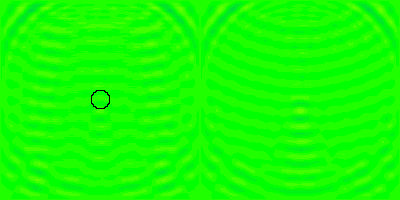
Illustration de la diffusion d'une onde électromagnétique par une sphère diélectrique de rayon comparable à la longueur d'onde et d'indice de réfraction relatif
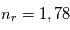
. Le champ électrique total figure à gauche, et la composante diffusée à droite.
Crédit :
R. Hogan (Univ. of Reading)
On regroupe les phénomènes d'absorption et de diffusion sous le nom d'extinction : ces deux phénomènes ont comme point commun de diminuer l'intensité d'un faisceau lumineux dans la direction d'incidence, soit en l'absorbant, soit en en déviant tout ou partie.
Régimes de Rayleigh et de Mie
Le régime de diffusion Rayleigh concerne la diffusion de la lumière par des particules petites devant la longueur d'onde (rayon 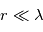 ), ce quelque soit le type d'aérosol (sphérique ou non) : molécules isolées de gaz, micro gouttes, etc.
), ce quelque soit le type d'aérosol (sphérique ou non) : molécules isolées de gaz, micro gouttes, etc.
La théorie de Mie est quant à elle valable pour toutes les valeurs de 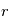 , mais uniquement pour des particules sphériques (gouttes liquides par exemple). Elle tend vers le cas Rayleigh lorsque
, mais uniquement pour des particules sphériques (gouttes liquides par exemple). Elle tend vers le cas Rayleigh lorsque 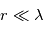 . Pour des particules non sphériques (cristaux, aérosols de Titan, poussières), cette théorie n'est valable qu'en première approximation, et les méthodes utilisées pour aller plus loin sont hors-programme.
. Pour des particules non sphériques (cristaux, aérosols de Titan, poussières), cette théorie n'est valable qu'en première approximation, et les méthodes utilisées pour aller plus loin sont hors-programme.
Section efficace de diffusion
Cette section efficace évolue de façon très différente selon le régime. Dans le régime Rayleigh, la section efficace est une fonction rapidement croissante de la longueur d'onde (une illustration courante étant la diffusion bien plus importante du bleu que de rouge dans l'atmosphère terrestre, donnant sa couleur à notre ciel). En régime de Mie, cette dépendance est bien plus faible, si bien que les diffuseurs apparaissent peu colorés en l'absence d'absorption (sur Terre, les nuages d'eau liquide sont un bon exemple).
Section efficace de diffusion
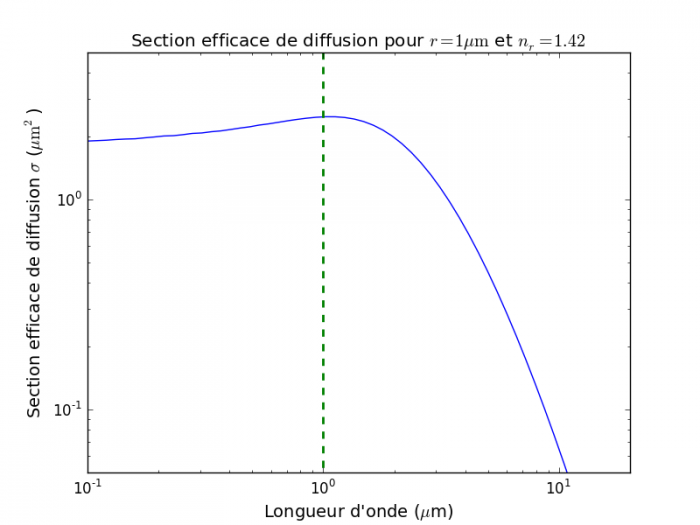
Représentation log-log de la section efficace de diffusion en fonction de la longueur d'onde pour des particules sphériques d'un rayon
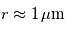
. Aux grandes longueurs d'onde,
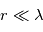
et on se trouve dans le régime
Rayleigh (
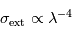
, apparaissant comme une asymptote de pente -4). Pour
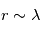
et
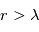
, on se trouve dans le régime de
Mie, où la section efficace est presque indépendante de
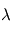
et voisine de la section géométrique des particules.
Crédit :
Loïc Rossi CC-BY-SA
Fonction de phase
La fonction de phase définit la répartition angulaire du rayonnement diffusé. C'est en quelque sorte la probabilité pour un rayon incident d'être diffusé dans une direction donnée.
Fonctions de phase de Rayleigh et de Mie

Figure montrant les indicatrices des différents processus de diffusion. La lumière incidente est supposée aller de gauche à droite. Plus la flèche est longue, plus la diffusion sera importante dans cette direction. À gauche, le régime de Rayleigh avec une diffusion relativement isotrope. Au centre, la diffusion de Mie, qui diffuse fortement vers l'avant. À droite, la diffusion de Mie pour des particules encore plus grandes.
Crédit :
Sharayanan CC-BY-SA
Types de réflexion
Quand du rayonnement parvient à une surface, il peut être réfléchi de plusieurs façons :
- Lambertienne, si les défauts de la surface sont supérieurs à la longueur d'onde du rayonnement incident. La lumière est alors réfléchie dans toutes les directions de façon homogène, on parle alors de surface lambertienne. Un mur blanc est un exemple de surface lambertienne ;
- Spéculaire, si les défauts sont très petits devant la longueur d'onde : la surface agit alors comme un miroir à la longueur d'onde considérée. Une surface liquide (une mer calme) peut agir comme une surface de réflexion spéculaire.
Réflexion diffuse et spéculaire

Photographie de la Terre prise depuis la station spatiale internationale. On distingue nettement la réflexion spéculaire sur la surface de l'océan et celle diffuse due aux nuages ou à la surface des continents.
Spectroscopie
Selon la longueur d'onde, le rayonnement incident sur une surface peut-être réfléchi mais aussi absorbé. On pourra alors étudier la réflectance d'une surface en fonction de la longueur d'onde (la réflectance valant 1 si tout la lumière est réfléchie ; 0 si tout est absorbé.).
L'étude de la réflectance d'une surface en fonction de la longueur d'onde peut être utile pour caractériser celle-ci. Ainsi certains minéraux ont un spectre avec des bandes d'absoption caractéristiques. C'est ce qui permet de caractériser des surfaces comme celles de Mars (pour détecter des minéraux hydratés par exemple), de la Lune ou bien celle d'astéroïdes et de comètes.
Intérêt
Son intérêt principal réside dans l'interprétation des spectres thermiques issus d'un objet (ici une planète et son atmosphère). En effet, sous réserve de certaines hypothèses :
- Absence de diffusion Toute extinction du rayonnement thermique est due à son absorption.
- Absorbant uniformément mélangé et de section efficace indépendante de la pression.
- Atmosphère en équilibre hydrostatique et isotherme en géométrie plan-parallèle (courbure planétaire négligée). L'hypothèse isotherme n'est ici requise que d'un point de vue hydrostatique, pas d'un point de vue radiatif.
La température de brillance correspond alors à la température du milieu situé à une profondeur optique égale à 1 : ![T_B(\lambda) \approx T\left[\tau(\lambda) = 1\right]](../pages_flux-et-spectre/equations_trans-rad/equation41.png) avec
avec 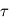 comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :
comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :
- les couches situées à des profondeurs optiques trop grandes devant 1 ne contribuent que faiblement car leur émission est trop atténuée selon la loi de Beer-Lambert.
- l'émission thermique des couches situées à faible profondeur optique est quant à elle peu atténuée, mais hélas trop peu intense pour contribuer significativement au rayonnement reçu (la loi de Kirchhoff impose que les bons émetteurs thermiques doivent aussi être de bons absorbants).
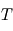 (on peut voir alors leur interaction comme celle d'un gaz de photons perpétuellement absorbés et émis par la matière environnante, et se mettant en équilibre de la sorte). Il existe également des phénomènes d'émission non thermiques (ex: fluorescence, émission laser), mais ils sortent du cadre de ce cours ; certains de ces processus sont vus dans ce chapitre.
(on peut voir alors leur interaction comme celle d'un gaz de photons perpétuellement absorbés et émis par la matière environnante, et se mettant en équilibre de la sorte). Il existe également des phénomènes d'émission non thermiques (ex: fluorescence, émission laser), mais ils sortent du cadre de ce cours ; certains de ces processus sont vus dans ce chapitre.
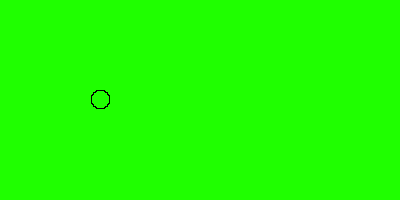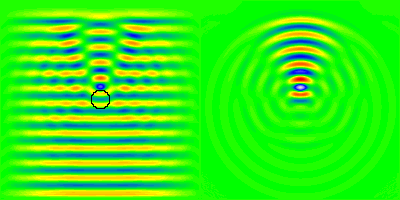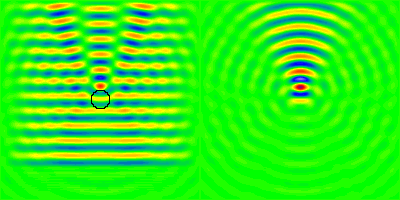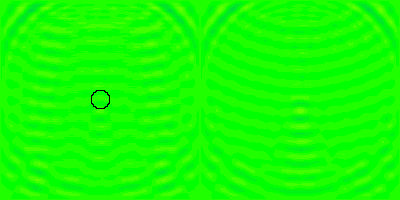
 . Le champ électrique total figure à gauche, et la composante diffusée à droite.
. Le champ électrique total figure à gauche, et la composante diffusée à droite.


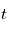 comme le rapport entre l'intensité lumineuse
comme le rapport entre l'intensité lumineuse 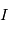 après traversée et celle
après traversée et celle 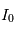 avant la traversée du milieu :
avant la traversée du milieu : 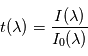 . Cette transmittance vaut 1 si le milieu traversé est transparent, 0 si le milieu est parfaitement opaque, et prend une valeur intermédiaire si le milieu est partiellement opaque. Elle dépend a priori de la longueur d'onde comme la formule l'indique.
. Cette transmittance vaut 1 si le milieu traversé est transparent, 0 si le milieu est parfaitement opaque, et prend une valeur intermédiaire si le milieu est partiellement opaque. Elle dépend a priori de la longueur d'onde comme la formule l'indique.
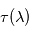 qui se déduit de la transmittance comme suit :
qui se déduit de la transmittance comme suit : ![\tau(\lambda) = - \ln \left[ t(\lambda) \right]](../pages_flux-et-spectre/equations_trans-rad/equation8.png) , soit
, soit 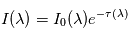 . Il est alors facile de déduire des propriétés mathématiques du logarithme que
. Il est alors facile de déduire des propriétés mathématiques du logarithme que 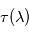 est une grandeur additive le long d'un même rayon (voir figure ci-contre), et qu'elle offre donc un paramétrage naturel de l'abscisse curviligne le long de ce rayon. Il est en outre possible de relier physiquement la variation locale de
est une grandeur additive le long d'un même rayon (voir figure ci-contre), et qu'elle offre donc un paramétrage naturel de l'abscisse curviligne le long de ce rayon. Il est en outre possible de relier physiquement la variation locale de 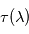 le long d'un rayon à la présence de matière traversée : c'est la loi de Beer-Lambert .
le long d'un rayon à la présence de matière traversée : c'est la loi de Beer-Lambert .
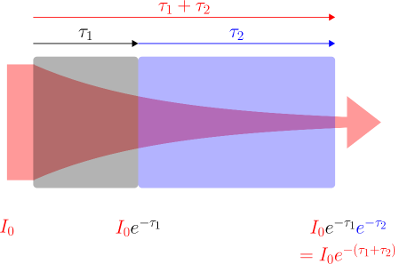
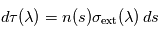 où
où 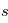 désigne l'abscisse curviligne le long du rayon (croissant dans le sens de propagation),
désigne l'abscisse curviligne le long du rayon (croissant dans le sens de propagation), 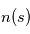 la densité volumique de diffusants et/ou absorbants et
la densité volumique de diffusants et/ou absorbants et 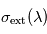 la section efficace d'extinction des diffusants et/ou absorbants. En présence de plusieurs types de diffuseurs et/ou d'absorbeurs, il suffit d'ajouter leurs contributions individuelles. L'évolution de la profondeur optique totale
la section efficace d'extinction des diffusants et/ou absorbants. En présence de plusieurs types de diffuseurs et/ou d'absorbeurs, il suffit d'ajouter leurs contributions individuelles. L'évolution de la profondeur optique totale 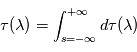 selon la longueur d'onde au cours d'une occultation ou d'un transit offre donc la possibilité à l'observateur de déduire les propriétés matérielles du milieu traversé (densité volumique et nature physique des particules responsables de l'extinction).
selon la longueur d'onde au cours d'une occultation ou d'un transit offre donc la possibilité à l'observateur de déduire les propriétés matérielles du milieu traversé (densité volumique et nature physique des particules responsables de l'extinction).
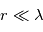 ), ce quelque soit le type d'aérosol (sphérique ou non) : molécules isolées de gaz, micro gouttes, etc.
), ce quelque soit le type d'aérosol (sphérique ou non) : molécules isolées de gaz, micro gouttes, etc.
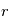 , mais uniquement pour des particules sphériques (gouttes liquides par exemple). Elle tend vers le cas Rayleigh lorsque
, mais uniquement pour des particules sphériques (gouttes liquides par exemple). Elle tend vers le cas Rayleigh lorsque 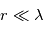 . Pour des particules non sphériques (cristaux, aérosols de Titan, poussières), cette théorie n'est valable qu'en première approximation, et les méthodes utilisées pour aller plus loin sont hors-programme.
. Pour des particules non sphériques (cristaux, aérosols de Titan, poussières), cette théorie n'est valable qu'en première approximation, et les méthodes utilisées pour aller plus loin sont hors-programme.

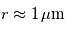 . Aux grandes longueurs d'onde,
. Aux grandes longueurs d'onde, 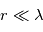 et on se trouve dans le régime Rayleigh (
et on se trouve dans le régime Rayleigh (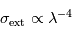 , apparaissant comme une asymptote de pente -4). Pour
, apparaissant comme une asymptote de pente -4). Pour 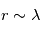 et
et 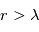 , on se trouve dans le régime de Mie, où la section efficace est presque indépendante de
, on se trouve dans le régime de Mie, où la section efficace est presque indépendante de 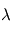 et voisine de la section géométrique des particules.
et voisine de la section géométrique des particules.

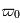 comme la proportion du rayonnement qui est diffusée. Si
comme la proportion du rayonnement qui est diffusée. Si 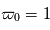 , toute la lumière est diffusée, il n'y a pas d'absorption. En revanche si
, toute la lumière est diffusée, il n'y a pas d'absorption. En revanche si 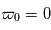 , tout la lumière est absorbée, il n'y a plus de diffusion. En général,
, tout la lumière est absorbée, il n'y a plus de diffusion. En général, 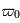 dépend de la longueur d'onde :
dépend de la longueur d'onde : 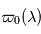 .
.

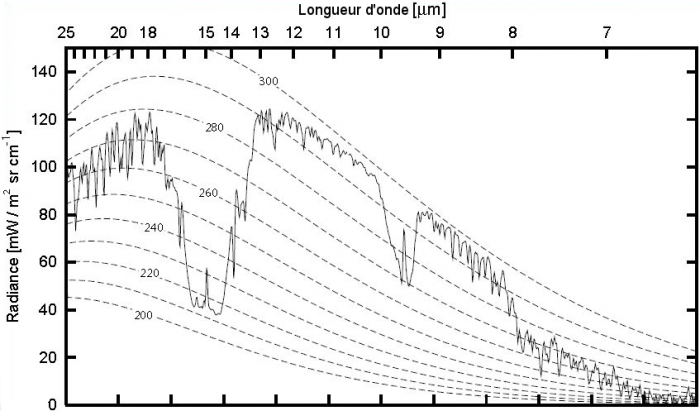
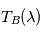 d'un objet est la température du corps noir qui émettrait la même intensité que celle émise par l'objet à la longueur d'onde
d'un objet est la température du corps noir qui émettrait la même intensité que celle émise par l'objet à la longueur d'onde 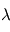 :
: ![I(\lambda) = B\left[\lambda, T_B(\lambda) \right]](../pages_flux-et-spectre/equations_trans-rad/equation33.png) où
où ![B\left[\lambda, T \right]](../pages_flux-et-spectre/equations_trans-rad/equation34.png) désigne la fonction de Planck à la longueur d'onde
désigne la fonction de Planck à la longueur d'onde 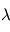 pour un corps noir de température
pour un corps noir de température 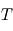 . Comme les courbes représentant les fonctions de Planck ne se croisent jamais, il y a correspondance unique entre
. Comme les courbes représentant les fonctions de Planck ne se croisent jamais, il y a correspondance unique entre 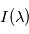 et
et 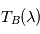 : la température de brillance n'est qu'une autre façon de décrire un spectre. En particulier, elle ne représente pas forcément la température d'un objet physique.
: la température de brillance n'est qu'une autre façon de décrire un spectre. En particulier, elle ne représente pas forcément la température d'un objet physique.
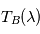 selon la formule
selon la formule 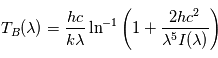 .
.
![T_B(\lambda) \approx T\left[\tau(\lambda) = 1\right]](../pages_flux-et-spectre/equations_trans-rad/equation41.png) avec
avec 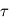 comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :
comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :